5. Литература 1, 4 

ЛАБОРАТОРНАЯ РАБОТА № 4

Исследование пассивного четырехполюсника.

1. Цель работы

Изучение пассивного четырехполюсника, его экспериментальное исследование, определение Z и Y-параметров четырехполюсников.

2. Теория

Во многих практических случаях анализ электрических цепей ограничивается расчетом токов и напряжений на отдельных участках цепи или нахождением уравнений связи между этими токами и напряжениями.

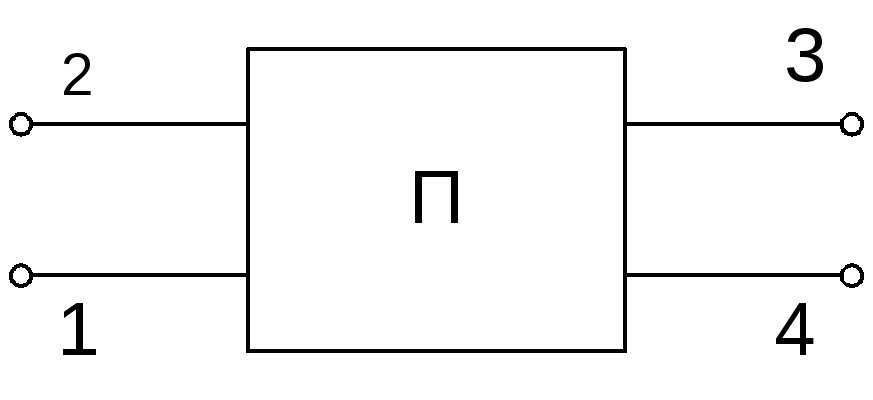
Рис. 1

Поэтому при анализе электросхем нашли широкое применение эквивалентные схемы, имеющие два входных (1-2) и два выходных контакта (3-4), которые называются четырехполюсниками (рис. 1). Четырехполюсник - это часть электрической схемы между четырьмя узлами.

Это некоторый обобщенный элемент схемы замещения ("черный ящик"), эквивалентно заменяющий целую схему. Четырехполюсник используется и в схемах замещения, и в принципиальных электросхемах. Четырехполюсники, в состав которых входят только пассивные элементы (индуктивности, емкости, сопротивления), называются пассивными. К пассивным четырехполюсникам относятся трансформатор, линия электропередачи, аттенюатор, частотный фильтр и т.д.

Если в четырехполюснике, кроме пассивных элементов, содержатся также источники электрической энергии, то он называется активным. Если обычные элементы характеризуются одним параметром (R, L, C, E и т.д.), то четырехполюсник характеризуется матрицей параметров (тензором). Эти матрицы называются системой параметров или формой. Форма четырехполюсника - это вид связи между токами и напряжениями на его входе и выходе.

Рассмотрим основные уравнения для пассивных четырехполюсников. Для этого в произвольной схеме с двумя источниками ЭДС Е₁ и Е₂ (рис. 2) выделим две ветви с источниками Е₁ и Е₂. Остальную часть схемы представим в виде пассивного четырехполюсника. Между токами и напряжениями ветвей I₁, U₁ и I₂, U₂ можно составить 6 линейных комбинаций (систем уравнений). Каждая из них будет характеризоваться своей матрицей (системой параметров). Они получили названия A, Y, Z, H, G, B формы. Наибольшее распространение получили A, Y, Z, H формы.

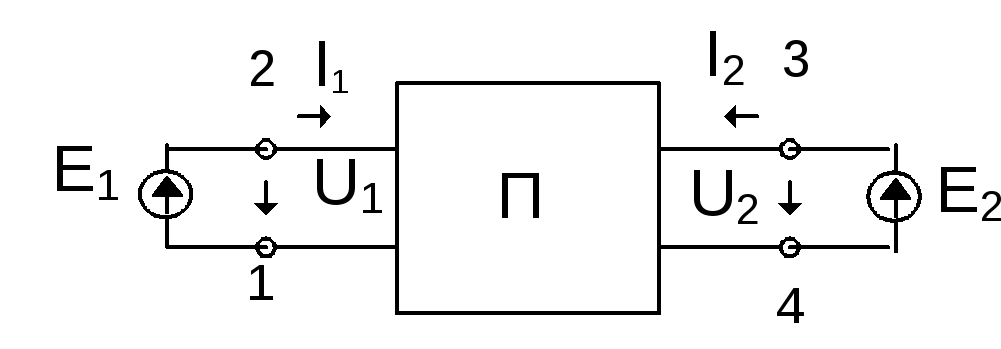
Рис. 2

Уравнения связи между I₁, U₁ и I₂, U₂ можно составить, например, используя метод контурных токов.

E₁ = -U₁ = Z₁₁I₁ + Z₁₂I₂ (1)

E₂ = -U₂ = Z₂₁I₂ + Z₂₂I₂

Эта форма записи уравнений называется Z-формой. Форма Z удобна при исследовании режимов четырехполюсников при их последовательном соединении. В матричной форме записи уравнение Z-формы имеет вид:

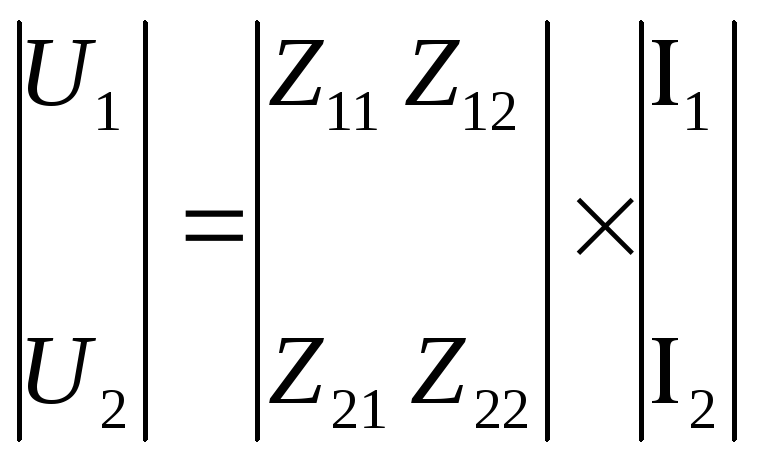(2)

Физический смысл элементов матрицы Z – некоторые импедансы.

Если функциями будут токи, а аргументами - напряжения, то мы получим Y-форму:

I₁ = Y₁₁U₁ + Y₁₂U₂

(3)

I₂ = Y₂₁U₁ + Y₂₂U₂

Между элементами матриц различных форм существует однозначная связь. Зная одну форму четырехполюсника, мы можем найти любую другую. Например, связь между Y и Z формами имеет следующий вид:

(4)

Физический смысл элементов матрицы Y – некоторые проводимости. Она удобна при исследовании четырехполюсников, соединенных параллельно. В матричном виде Y-форма имеет вид:

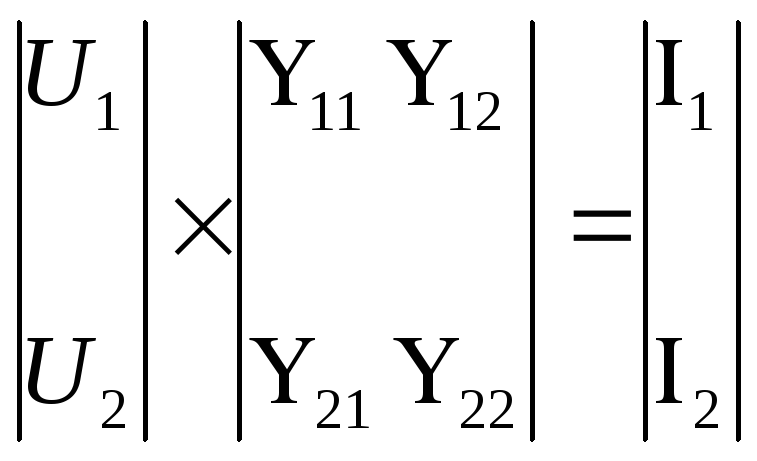(5)

В А-форме входное напряжение U₁ и ток I₁ выражены через U₂ и I₂ . Она чаще всего используется при исследовании четырехполюсников при их каскадном соединении.

Для H-формы функциями служат U₁ и I₂, а аргументами I₁ и U₂. Она используется при последовательно-параллельном соединении четырехполюсников.

Четырехполюсник называется симметричным, если при замене входных и выходных контактов токи и напряжения на входе и выходе не меняются, т. е. уравнения остаются неизменными при перестановке индексов переменных. Для этого необходимо, чтобы матрицы параметров были симметричны, т. е. Y₁₂ = Y₂₁, Z₁₂ = Z₂₁, A₁₂ = A₂₁, H₁₂ = H₂₁.

Все четырехполюсники, не удовлетворяющие этому условию, называются несимметричными. Четырехполюсники, у которых недиагональные элементы равны по модулю, но имеют разные знаки (Y₁₂ = -Y₂₁ и Z₁₂ = -Z₂₁ …), называют взаимными.

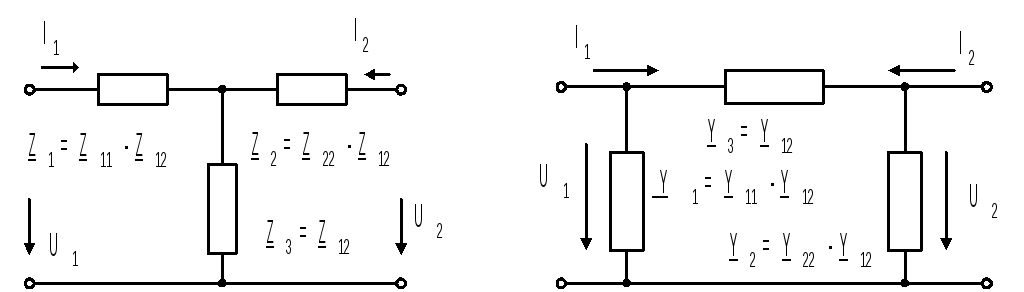
Пользуясь уравнениями форм четырехполюсников, можно получить различные схемы замещения, которые облегчают исследование основных свойств соответствующих цепей. Для пассивных цепей имеются два основных вида схем замещения: Т-образная (рис. 3а) и П-образная

(рис. 3б).

а б

Рис. 3

Для Т-схемы замещения ее параметры проще всего найти из Z-формы (рис. 3 а), для П-образной из Y-формы (рис. 3 б).

Уравнения для элементов схем замещения получаются из уравнений соответствующих форм при требовании эквивалентности, т.е. схема замещения не должна изменять ни токов, ни напряжений во внешней цепи U₁, I₁, U₂, I₂. Если четырехполюсник содержит реактивные элементы (L и C) и работает с переменными токами, то все описанные выше величины, согласно символическому методу анализа, необходимо считать двумерными векторами и комплексными величинами.

Относительно входных и выходных цепей четырехполюсник представляет собой два двухполюсника. По теореме об эквивалентном генераторе эти двухполюсники можно представить последовательно соединенными ЭДС и сопротивлением. Т. о., четырехполюсник можно эквивалентно представить двумя связанными двухполюсниками (рис. 4). Это эквивалентная схема четырехполюсника.

Z_вх и Z_вых - входное и выходное сопротивления (импедансы), E₁ = -U₁, E₂ = -U₂. Входные и выходные импедансы по определению равны: Z_вх = U₁/I₁ Z_вых = U₂/I₂. В режиме холостого хода и короткого замыкания можно вычислить Z_вх и Z_вых из известных параметров четырехполюсника.

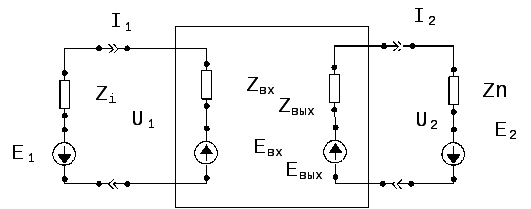
Рис. 4

Например, зная Н-параметры:

U₁ = H₁₁I₁ + H₁₂U₂

(6)

I₂ = H₂₁I₁ + H₂₂U₂ ,

можно найти:

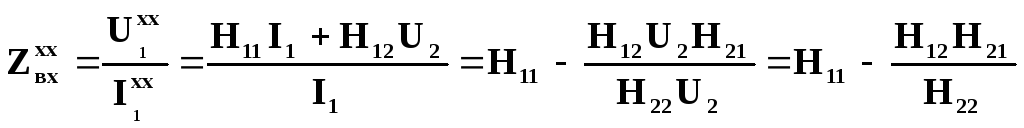(7)

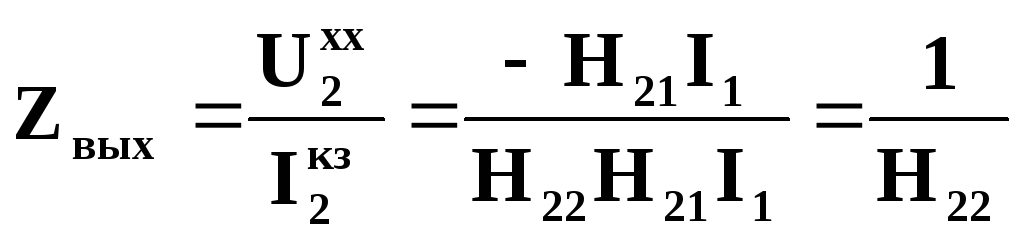(8)

Видно, что Z_вх и Z_вых могут быть неодинаковыми. Это используется для согласования выходного сопротивления цепи с входным сопротивлением другой цепи при их соединении через согласующий четырехполюсник. При подключении нагрузки Z_n (рис. 4) и источника с внутренним сопротивлением Z_i, Z_вх и Z_вых изменяются:

(9)

(10)

Четырехполюсник чаще всего работает как передаточное звено цепи. Поэтому важное значение имеют коэффициенты передачи по напряжению K_U = U₂/U₁, по току K_I = I₂/I₁ и по мощности K_p = P₂/P₁. Эти величины также зависят от Z_i и Z_n:

(11)

(12)

Экспериментально форму четырехполюсника проще всего определить, используя экстремальные режимы его работы – холостой ход (хх) и короткое замыкание (кз). Для холостого хода I₂ = 0, поэтому из уравнения (1) получим:

Z₁₁ = U₁^хх/I₁^хх;

Z₂₁ = U₂^хх/I₁^хх (13)

Если поменять местами входные и выходные контакты, т.е. когда четырехполюсник питается со стороны контактов 3-4, а 1-2 разомкнуты (холостой ход на входе), то I₁ = 0 и можно записать:

Z₂₂ = U₂^хх/I₂^хх; Z₁₂ = U₁^хх/I₂^хх (14)

Аналогично можно получить уравнения для Y-формы, используя режим короткого замыкания U₂ = 0:

Y₁₁ = I₁^кз/U₁^кз; Y₂₂ = I₂^кз/U₂^кз (15)

При коротком замыкании входных узлов U₁ = 0, тогда получается:

Y₁₂ = I₁^кз/U₂^кз ; Y₂₁ = I₂^кз/U₁^кз (16)