, А фаза:. (17)

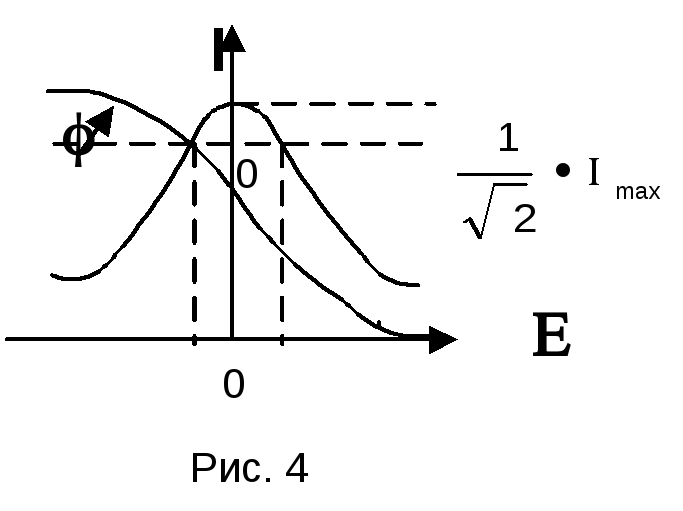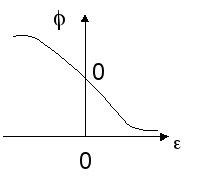
Выражения (17) получены из (15). Графики амплитуды тока и фазы показаны на рис. 4. Максимальное значение тока. На низких частотах,исопротивление контура имеет емкостный характер. На высоких частотах,сопротивление контура имеет индуктивный характер. При резонансе сопротивление контура чисто активное и равно R.

Из уравнений (16), (17) видно, что амплитуда тока уменьшится в раз при расстройке, равной:

.

При малых расстройках и приближенно можно записать:

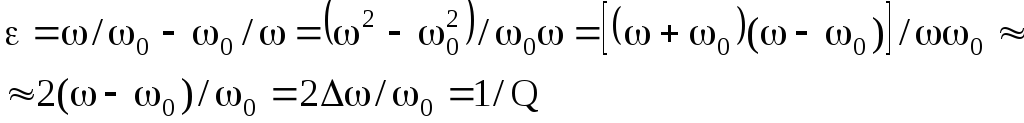(18)

Т.о., добротность определяет ширину резонансной кривой на уровне

≈0,707 или – 3 дБ.

Активная мощность цепи:

Реактивная мощность цепи:

Q_R = IUsin

Если sin> 0, то Q_R > 0 и при sin< 0, Q_R <0. Таким образом, реактивная мощность, потребляемая индуктивностью, положительна, а емкостью - отрицательна.

Полная мощность S = IU. Она измеряется в (ВА). Между P, Q_R и S существует соотношение S² = Q_R²+P².

Из определения добротности контура можно записать:

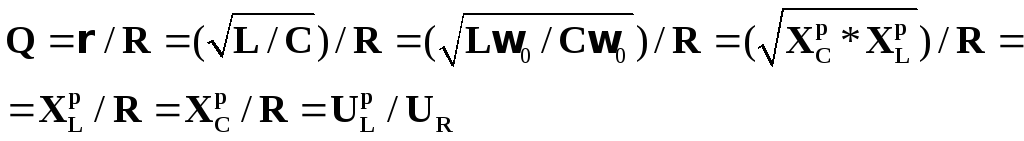(19)

Здесь индекс «р» показывает, что величины взяты при частоте резонанса. Т.о., добротность показывает, во сколько раз напряжение на индуктивности (или на емкости) превышает напряжение на активном сопротивлении в резонансном режиме. Из (19) так же видно, что добротность равна отношению реактивной (запасаемой в контуре) мощности к активной (теряемой). Практически в радиотехнических устройствах Q может доходить до 300 и выше. Величина, обратная добротности, называется затуханием = 1/Q.

Рассмотрим цепь с параллельным соединением R, L, C (рис. 5 а) (параллельный колебательный контур). Здесь возникает резонанс токов.

Напряжение на ветвях одинаковое, тогда ток будет равен векторной сумме токов. Векторная диаграмма показана на рис. 5 в.

Импеданс цепи равен:

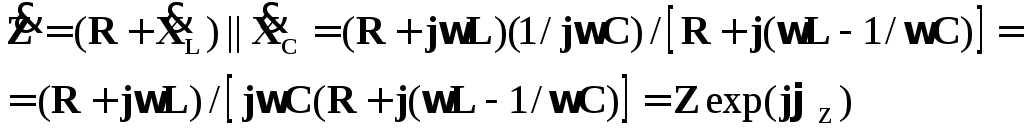(20)

Для простоты будем считать катушку индуктивности “хорошей”, т.е. R<<X_L=L для всех используемых частот. ТогдаZ можно приближенно записать:

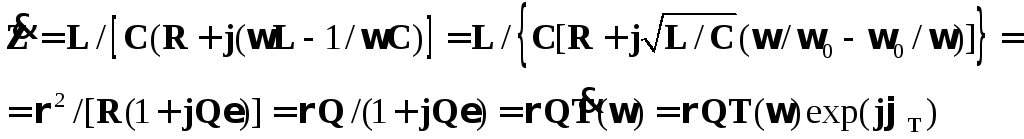(21)

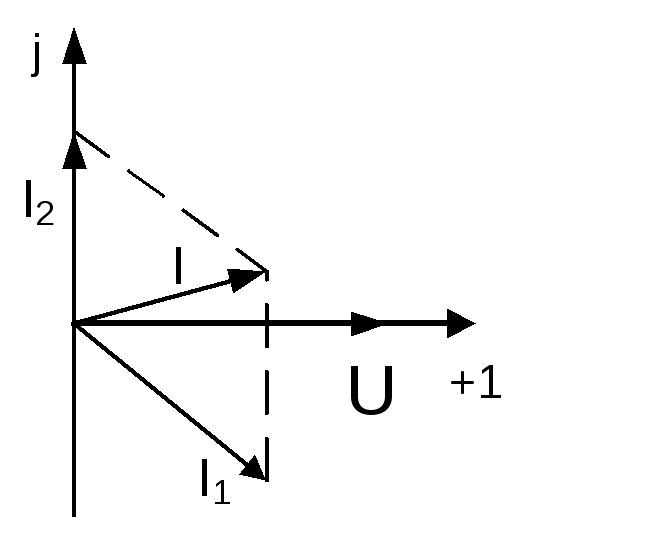
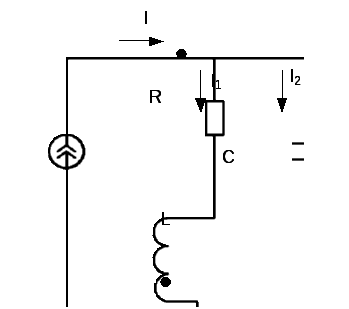
а) б)

Рис. 5

Здесь использованы введенные ранее понятия: собственная (резонансная) частота , характеристическое сопротивление, добротность Q и характеристическая функция T(.

Наш контур подсоединен к источнику тока (т.е. источнику электроэнергии с бесконечным внутренним сопротивлением). Найдем напряжение :

, (22)

где T(и_T определяются теми же уравнениями (16), что и для последовательного контура. При частоте резонанса ;и T(=1, тогда_T = 0.

Т.о. при резонансе токов токи через ветви I₁ и I₂компенсируют друг друга и напряжение принимает максимальное значение:

U_рез = I. (23)

Тогда формально можно считать, что при резонансе параллельный контур представляет собой активное сопротивление

R_Э = . (24)

R_Э – эквивалентное сопротивление контура. Зависимость U_m() полностью аналогична зависимости I_m(),() для последовательного контура (рис. 4).

Колебательные контуры используются в радиотехнике при решении одной из основных задач – для выделения или подавления определенной полосы частот, частотные свойства контура определяются его АХЧ – амплитудно-частотной (зависимостью тока I или U от частоты ), а также ФХЧ – фазо-частотной или фазовой характеристикой (зависимостью угла сдвига фаз между током и напряжением от частоты). Они полностью определяются характеристической функцией T(. Если расстройка невелика, то согласно (18) можно считать. На практике измеряют сами значения частоти действительные значенияU и I. Принято результаты представлять в нормированном виде или, где U_P и I_P значения параметров при резонансной частоте .

Н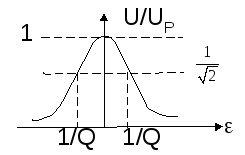а рис. 6 приведена типичная нормированная резонансная характеристика параллельного контура.

Рис. 6

В радиотехнике используют понятие полосы пропускания контура – интервала частот вблизи резонанса, на границе которого амплитуда тока снижается до 0,707(1/= -3дБ) от резонансного значения. Полоса пропускания равна 2. Зная, легко подсчитать добротность контура.

Резонансные характеристики последовательного и параллельного контуров одинаковы, т.к. все выражения для тока в последовательном контуре справедливы для напряжения в параллельном контуре.