
ядерная физика
.pdf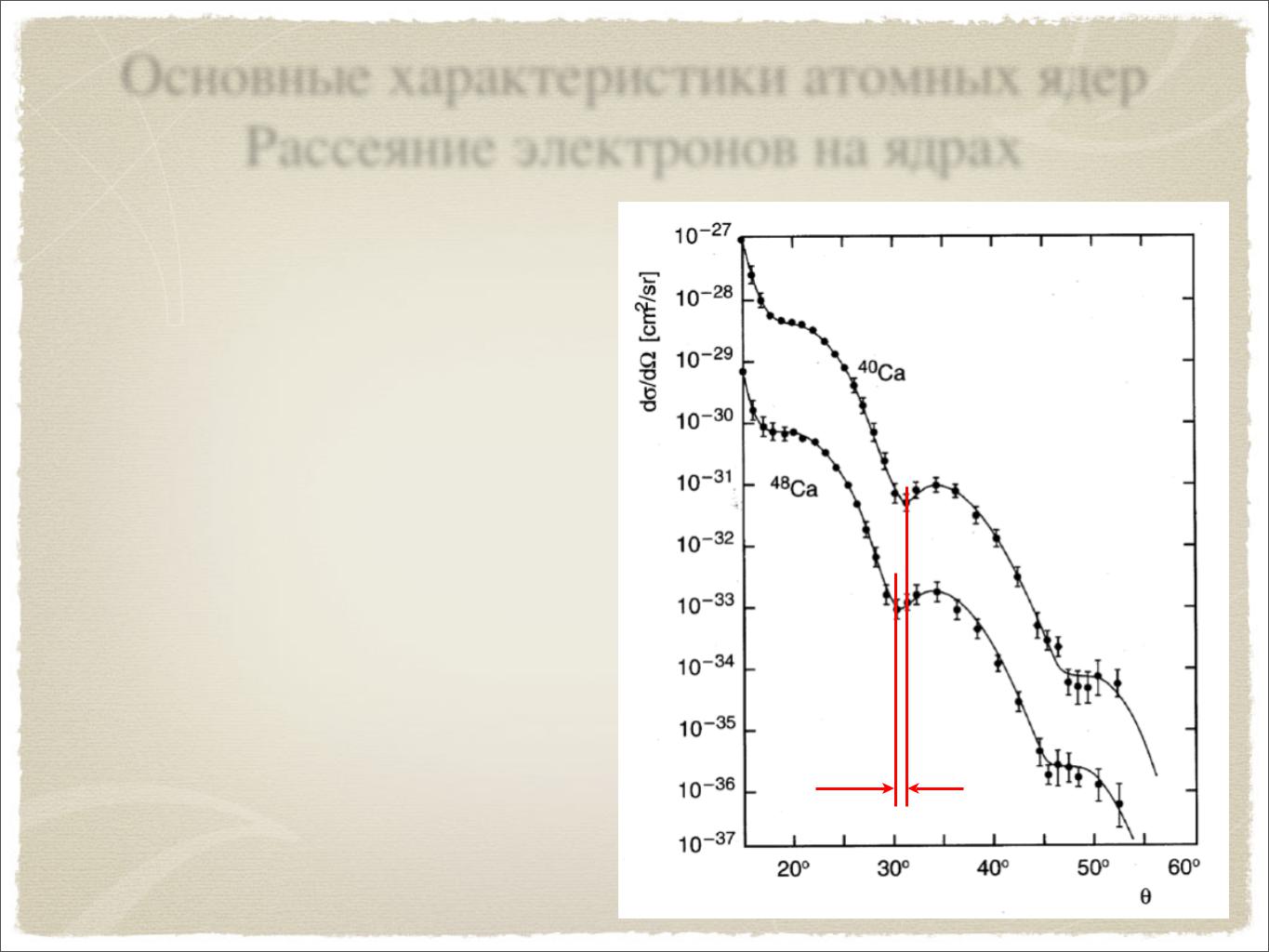
Основные характеристики атомных ядер Рассеяние электронов на ядрах
 Микрочастицы обладают волновыми свойствами λ=h/p (волна Де Бройля)
Микрочастицы обладают волновыми свойствами λ=h/p (волна Де Бройля)
 В случае рассеяния на сфере радиуса R, при условии λ≤R, возникает дифракционная картина
В случае рассеяния на сфере радиуса R, при условии λ≤R, возникает дифракционная картина
 Дифракционные минимумы имеют место
Дифракционные минимумы имеют место
при углах:
ΔΘ
sin Θmin≈n |
0.61 |
|
λ, n=1,2,3... |
|
R |
||||
|
|
|||
Основные характеристики атомных ядер Формфакторы
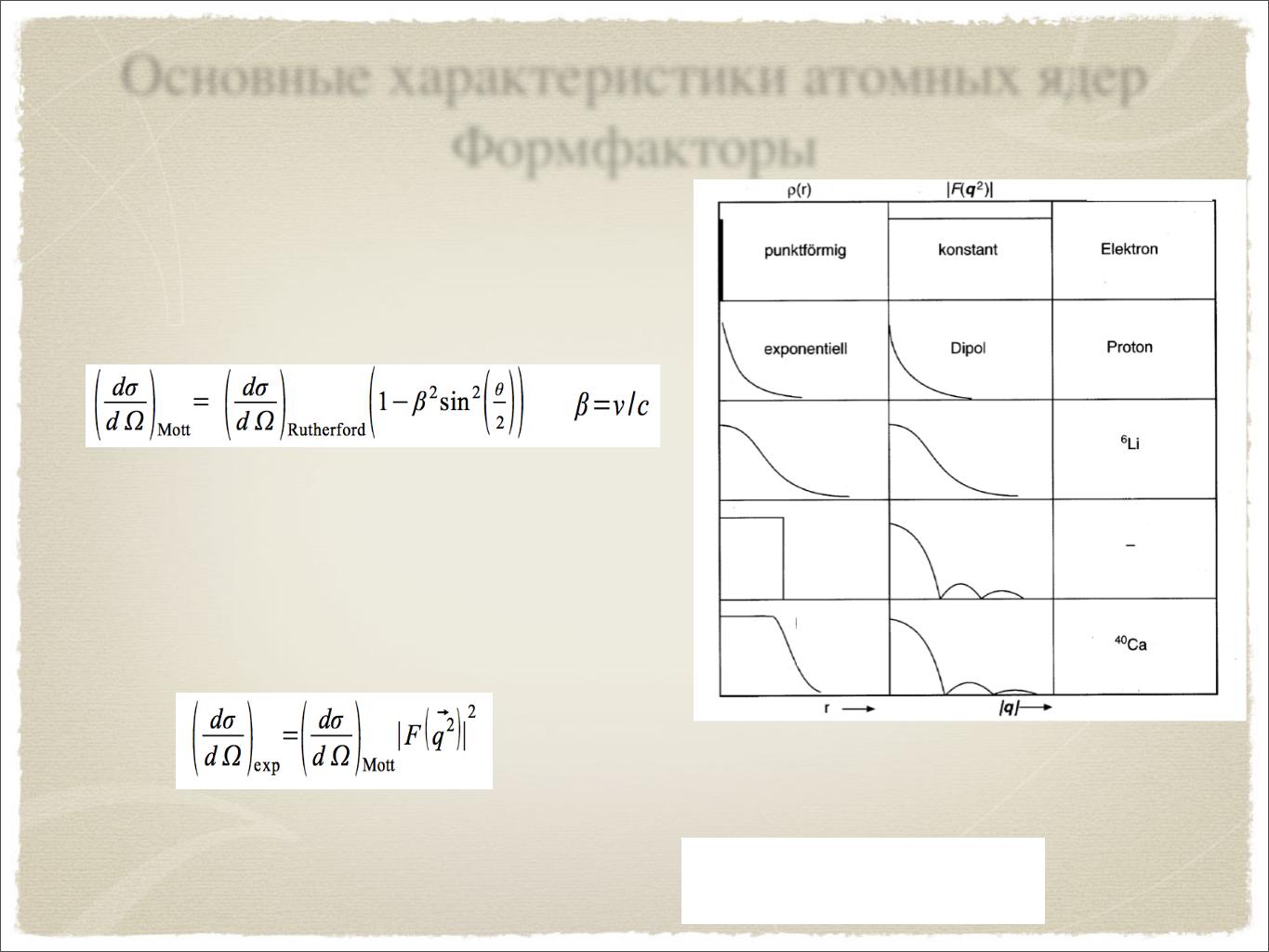
 Для учета спина электрона и релятивистских поправок используется формула Мотта
Для учета спина электрона и релятивистских поправок используется формула Мотта
|
|
|
частица или ядро |
|||
|
|
|
|
|
|
|
точечный |
|
|
|
|
|
|
|
постоянная |
|
|
электрон |
|
|
объект |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
экспонента |
|
|
|
протон |
|
|
|
|
|
гаусс
 В случае, если ядро обладает пространственной структурой, появляется добавочный множитель - формфактор F(q2)
В случае, если ядро обладает пространственной структурой, появляется добавочный множитель - формфактор F(q2)
однородная
сфера
распределение
Ферми
, q - переданный ядру импульс
 В случае упругого
В случае упругого
кулоновского формфактора F(q2) ∫ρ(r)eiqr/ħdv
Основные характеристики атомных ядер
Формфакторы
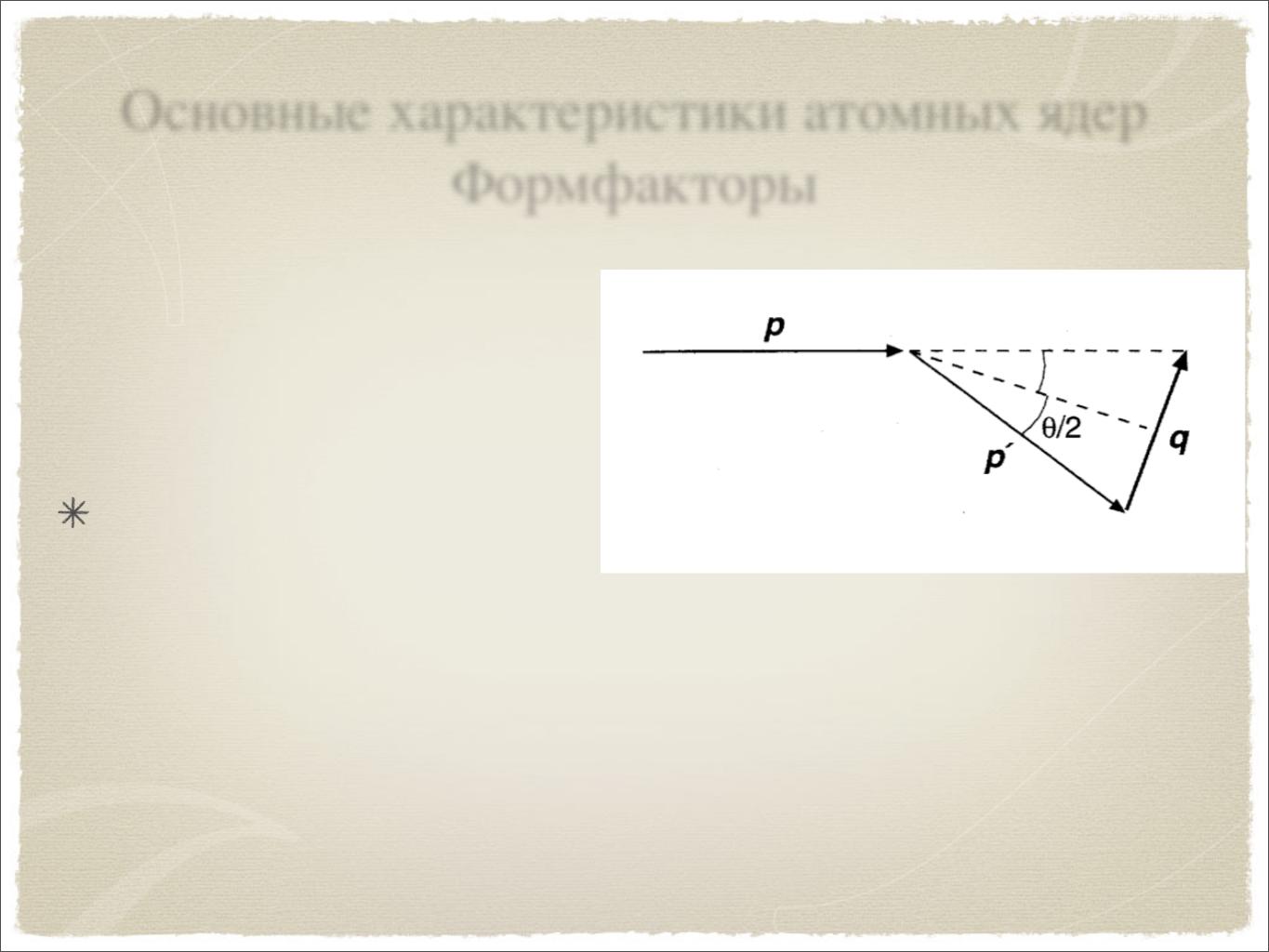
 Передаваемый при рассеянии импульс определяется как:
Передаваемый при рассеянии импульс определяется как:
|
|
q=| p p´ | |
|
|
|
|
|
|
|
|
|
В случае упругого |
|
||||
рассеяния величина |
р - импульс падающей частицы |
||||
переданного импульса |
|||||
связана с углом |
р´- импульс рассеянной частицы |
||||
рассеяния θ |
|
||||
соотношением: |
|
||||
|
|
q=2p·sin(θ/2) |
|
|
|
|
|
|
|
|
|
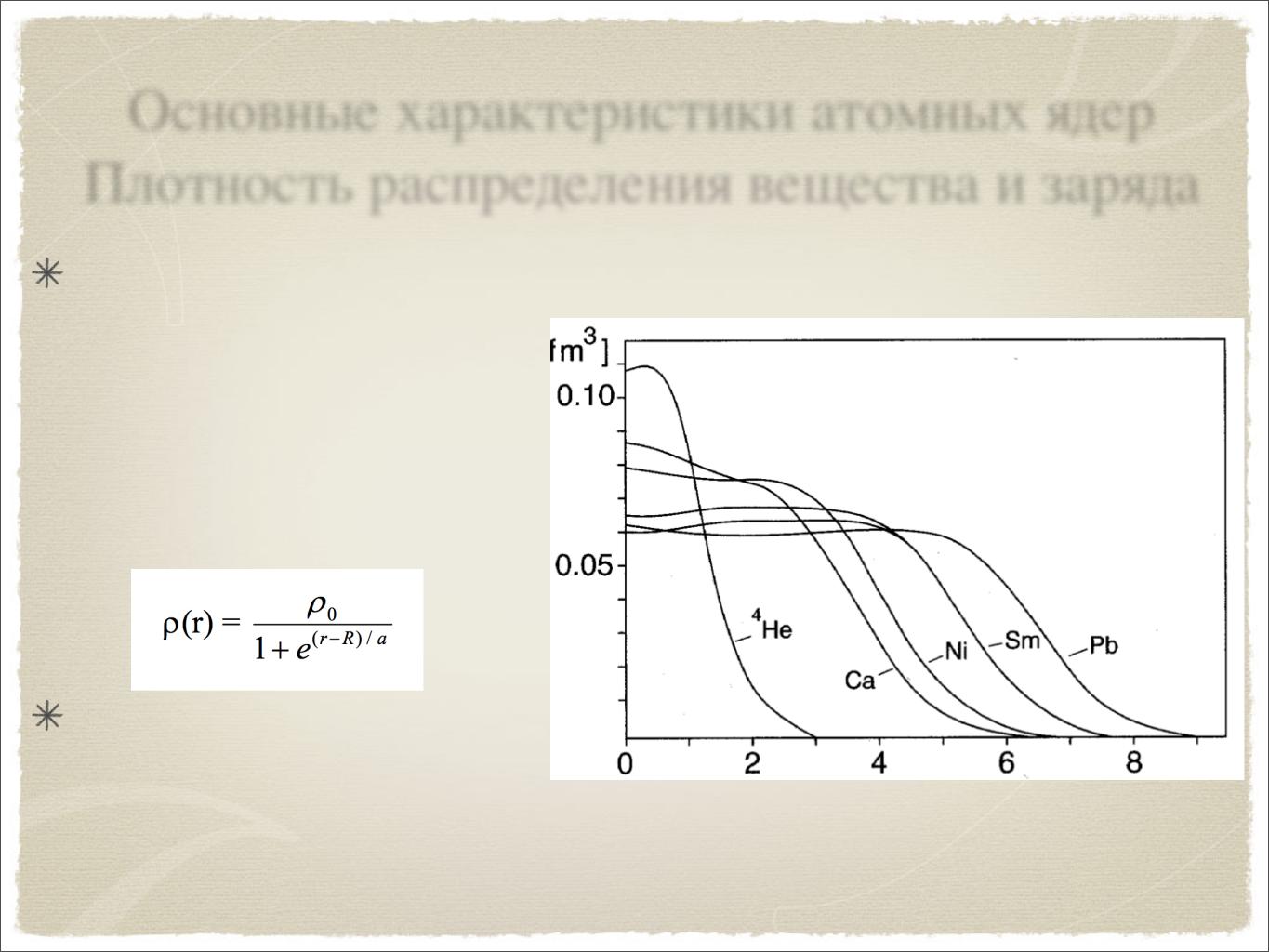
Основные характеристики атомных ядер Плотность распределения вещества и заряда
Распределение заряда |
|
|
|
и вещества в атомных |
фм-3 |
|
|
|
|
||
ядрах можно |
е. |
|
|
|
|
||
|
|
|
|
приблеженно описать |
|
|
|
двухпараметрическим |
|
|
|
распределенем Ферми |
|
|
распределения |
полуплотности) |
Плотность |
|
|
Величину R (радиус |
|
|
|
называют радиусом |
|
|
|
ядра |
|
|
|
150 |
208 |
56 |
|
40
заряда
Радиус фм
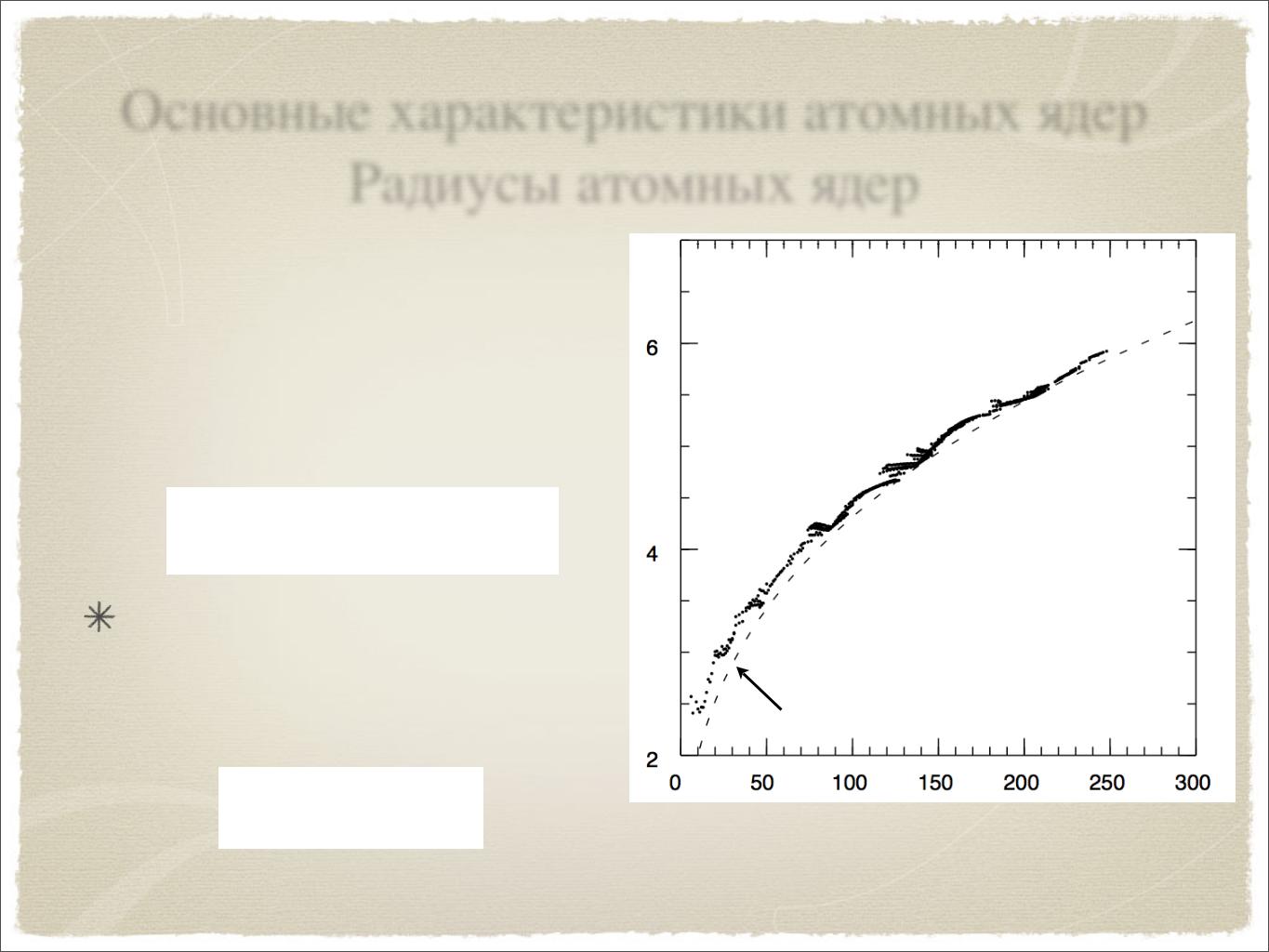
Основные характеристики атомных ядер Радиусы атомных ядер
Rch
Фм
 Радиус ядра приближенно может быть описан формулой
Радиус ядра приближенно может быть описан формулой
R=(1.2A⅓-0.5) Фм
Для ядер, с А > 20, |
|
|
радиус R с точностью не |
1.2A⅓ |
|
хуже 20% можно найти |
||
|
R≈1.2A⅓
А

Основные характеристики атомных ядер Радиусы атомных ядер. Гало.
11Li 208Pb
Ядерное гало - это один или два слабо связанных нуклона, находящихся на большом расстоянии от кора
11Be
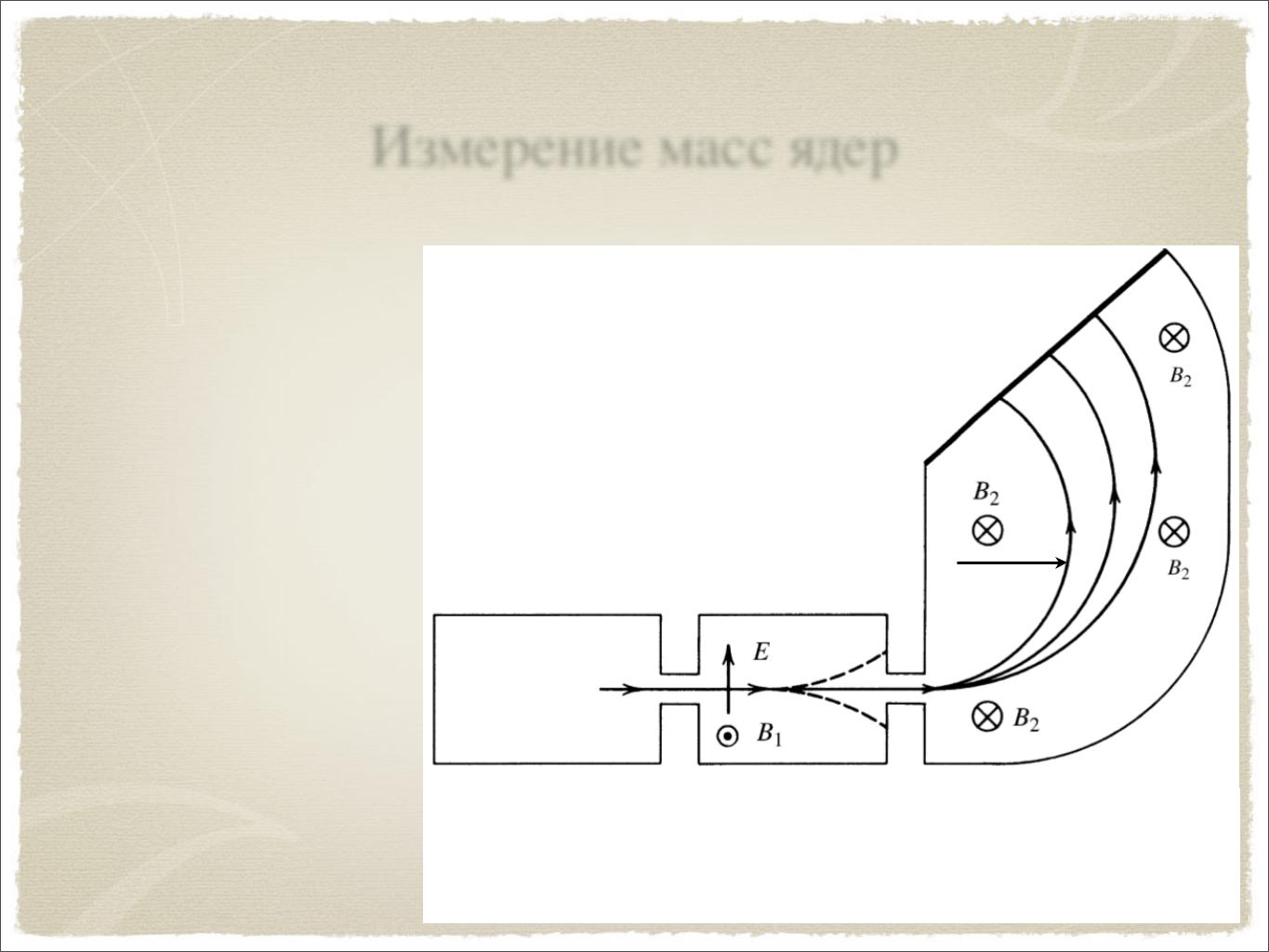
Измерение масс ядер
 В 1910 году первый спектрометр был сконструирован Дж. Дж. Томсоном
В 1910 году первый спектрометр был сконструирован Дж. Дж. Томсоном
 Более совершенная модель разработана Астоном в 1919 году.
Более совершенная модель разработана Астоном в 1919 году.
Mv=qB2R |
Детектор |
Определение массы |
|
ионов из условия |
|
Определение скорости ионов v из условия R
qE=qvB1
Источник ионов с зарядом q
и массами Mn
Сепаратор скоростей
сэлектрическим полем
Еи магнитным В1
В магнитном поле В2 ионы движутся по окружности радиуса R
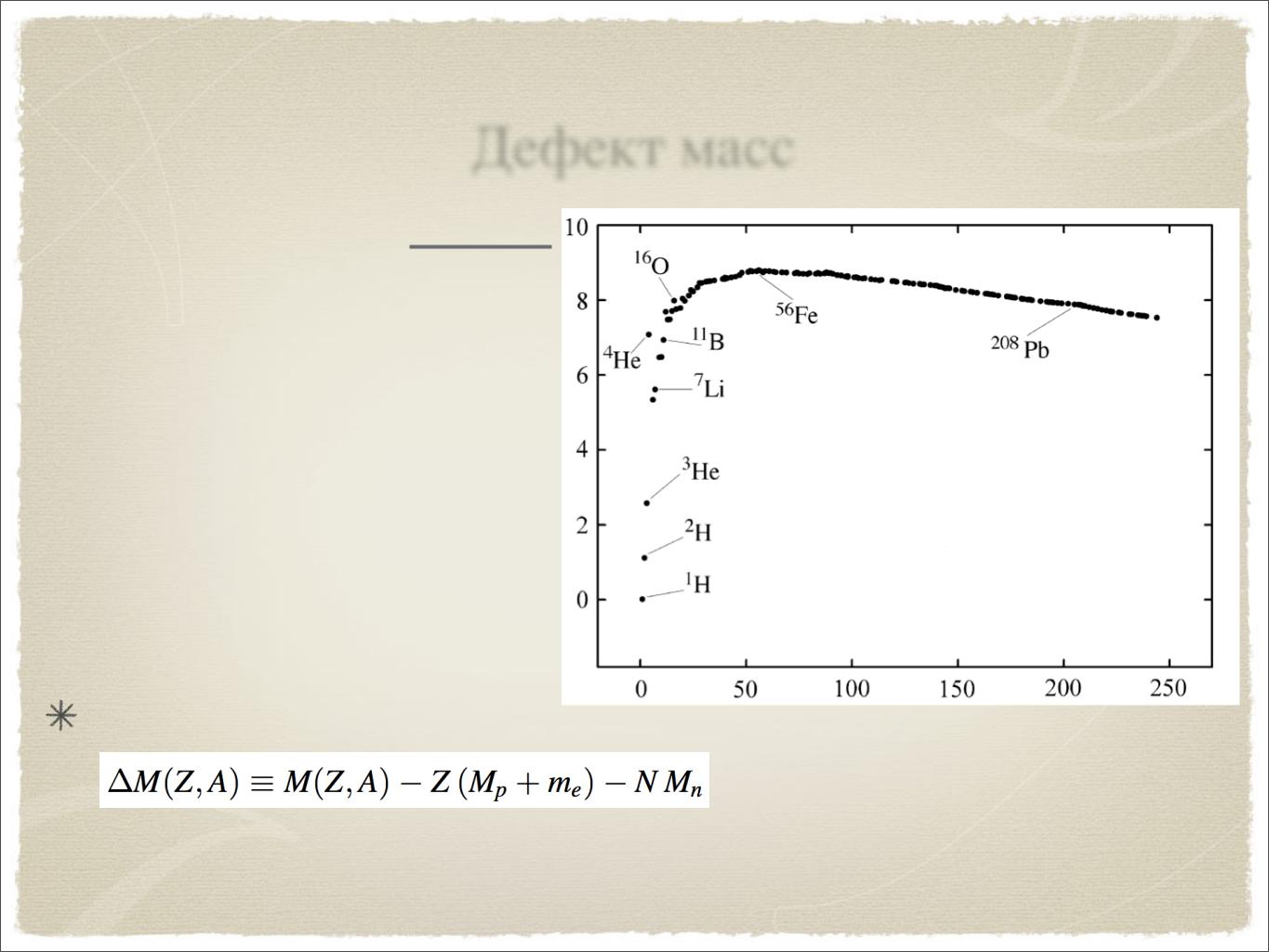
Дефект масс
 M(Z,A)c2
M(Z,A)c2
A
 Масса ядра не равна сумме масс Z протонов и N нейтронов
Масса ядра не равна сумме масс Z протонов и N нейтронов
Величина |
Массовое число А |
называется дефектом массы
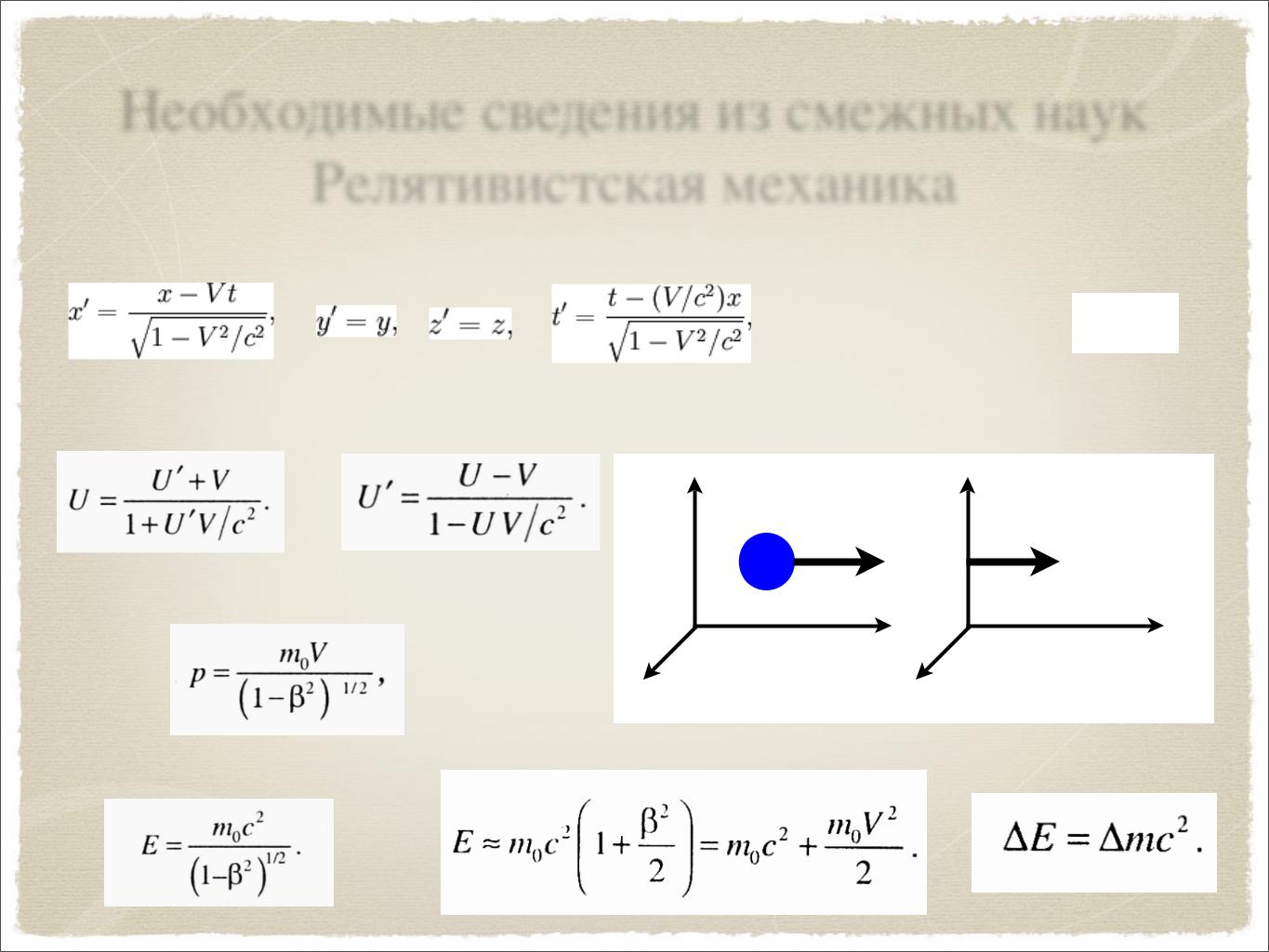
Необходимые сведения из смежных наук Релятивистская механика
 Преобразования Лоренца
Преобразования Лоренца
введем обозначение β=V/с
 Сложение скоростей
Сложение скоростей
y |
y′ |
U |
V |
 Релятивистский импульс
Релятивистский импульс
z |
x,t |
z′ |
x′,t′ |
 Энергия тела
Энергия тела

Необходимые сведения из смежных наук Квантовая механика
 Корпускулярно-волновой дуализм света
Корпускулярно-волновой дуализм света
Свет представляет собой поток фотонов, с энергией E=hν и импульсом p=E/c. Вводя круговую частоту ω=2πν и ħ=h/(2π), можно записать E=ħω, p=2πħ/λ=ħk, где λ=с/ν - длина волны, k=2π/λ - волновое число.
 Частицы, как квантово-механические объекты
Частицы, как квантово-механические объекты
Частицам тоже присущ корпускулярно-волновой дуализм:
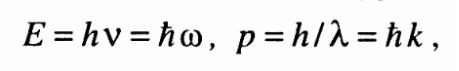 где E, p - энергия и импульс частицы, соответственно
где E, p - энергия и импульс частицы, соответственно
Свободно движущаяся частица описывается плоской волной ( волна де Бройля)
 Волновая функция
Волновая функция
Квадрат модуля волновой функции - вероятность найти частицу в области от x до (x+dx), от y до (y+dy), от z до (z+dz)
Условие нормировки
