Тема 2. Диференціальне числення
ФУНКЦІЙ ОДНІЄЇ ЗМІННОЇ
Похідна
2.1
Користуючись тільки визначенням
похідної, знайти
:
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
;
;
;
;
;
. 2.2.
Кількість електрики, яка проходить
крізь будь-який переріз провідника, є
функція від часу
.
Визначити середню величину струму за
проміжок часу
і, користуючись поняттям похідної ,
визначити величину струму в
момент часу
.
2.3.
Кількість радіоактивної величини є
функція часу
.
Користуючись поняттям похідної, дати
означення швидкості розпаду радіоактивної
величини.
2.4.
Для заданої функції
,
користуючись означенням однобічної
похідної, знайти
і
:
1)
;
2)
.
2.5. Знайти похідні наступних функцій:
|
1)
|
2)
|
|
3)
|
4)
|
|
5)
|
6)
|
;
;
;
;
.2.6. Знайти похідні наступних функцій:
|
1)
|
2) |
3)
|
|
4)
|
5)
|
|
;
;
;
;
.2.7. Знайти похідні наступних функцій:
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
;
;
;
;
;
.2.8. Написати рівняння дотичної до заданих кривих:
|
1)
|
2)
|
|
3)
|
4)
|
|
5)
|
|
|
6)
6)
|
|
у точці
;
у точці
;
у точці
;
у точці
;
у точках перетину з віссю
;
у точках перетину з віссю
. 2.9.
Визначити під яким кутом крива
перетинає вісь абсцис.
2.10.
Визначити в якій точці дотична до
параболи
паралельна прямій
.
2.11.
Тіло рухається по прямій
за законом
.
Визначити швидкість та прискорення
руху. В які моменти тіло змінює напрям
руху?
2.12.
Напруга конденсатора змінюється за
синусоїдальним законом
.
Обчислити величину зарядного струму
,
який протікає крізь конденсатор.
2.13. Застосовуючи попереднє логарифмування, знайти похідні функцій:
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
|
;
;
;
;
. 2.14.
Для функцій, заданих параметрично,
знайти
:
|
1)
|
2)
|
|
3)
|
4)
|
|
5) |
6)
|
;
;
;
;
;
.2.15. Знайти похідні від функцій, заданих неявно:
|
1)
|
2)
|
3) |
|
4)
|
5) |
6)
|
;
;
;
;
;
.
Диференціал. Похідні вищих порядків
2.16. Знайти диференціали функцій:
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
;
;
;
;
;
. 2.17.
Знайти приріст
з точністю до 0,001 і диференціал
з точністю до 0,1 функції
,
який відповідає значенню аргументу
і
.
2.18.
Ребра куба збільшені на 1 см. При цьому
диференціал
об’єму
дорівнює 12 см
.
Знайти первісну довжину ребер.
2.19.
Радіус кола збільшений на 1 см. Диференціал
площі кола дорівнює при цьому 6 см
.
Знайти первісну величину радіуса.
2.20.
Знайти наближений вираз для приросту
об’єму
прямого кругового циліндру з висотою
при зміні радіуса основи
на величину
.
2.21.
Довести наближену формулу
і обчислити за цією формулою 1,02
.
2.22. Вивести формулу для наближеного обчислення функцій:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
.
2.23. Обчислити наближено:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
.
2.24. Знайти похідні 2-го порядку від наступних функцій:
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
;
;
;
;
;
. 2.25.
Знайти
,
якщо
.
2.26.
Знайти формулу для
від наступних функцій:
1)
;
2)
;
3)
;
4)
;
5)
.
2.27.
Показати, що функція
задовольняє диференціальне рівняння
.
2.28.
Показати, що функція
задовольняє диференціальне рівняння
.
Теореми про диференційовані функції.
Правило Лопіталя. Формула Тейлора
2.29.
Довести, що між коренями функції
знаходиться корінь її похідної.
2.30.
У якій точці дотична до параболи
паралельна хорді, яка стягує точки
і
?
2.31.
Записати формулу Лагранжа для функції
на відрізку [0,1], знайти
на інтервалі (0,1) відповідне значення
.
2.32.
Розкрити невизначеність виду
:
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
;
;
;
;
;
.
2.33. Розкрити
невизначеність виду
:
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
;
;
;
;
;
. 2.34.
Розкрити невизначеність виду
:
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
;
;
;
;
. 2.35.
Розкрити невизначеність виду
:
|
1)
|
2)
|
|
3)
|
4)
|
;
;
;
. 2.36.
Розкрити невизначеність виду (
),
,
:
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
;
;
;
;
;
. 2.37.
Написати формулу Тейлора 3-го порядку
для функції
в точці
.
2.38.
Написати формулу Тейлора 6-го порядку
для функції
.
2.39. Обчислити з точністю до 0,001 наближене значення наступних чисел:
1)
;
2)
;
3)
;
4)
.
2.40.
Многочлен
розкласти за степенями двочлена
.
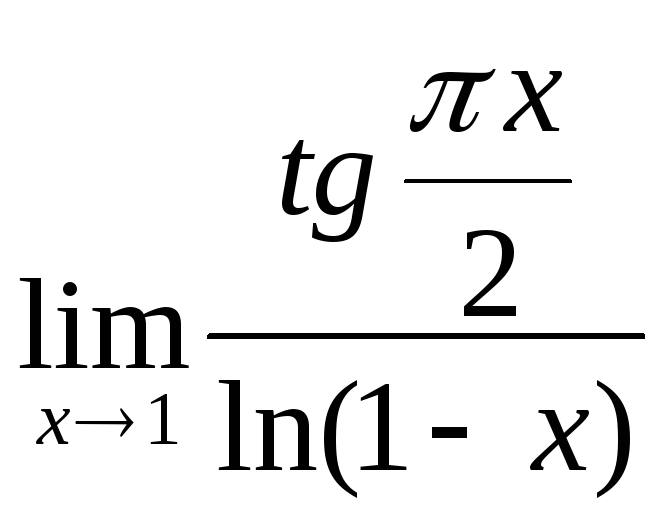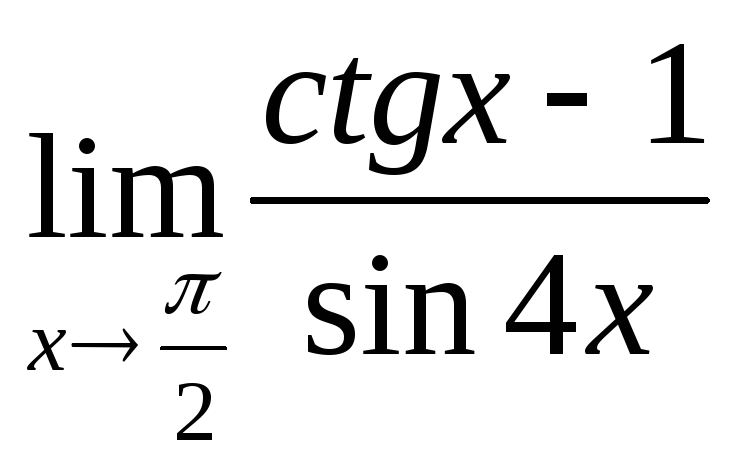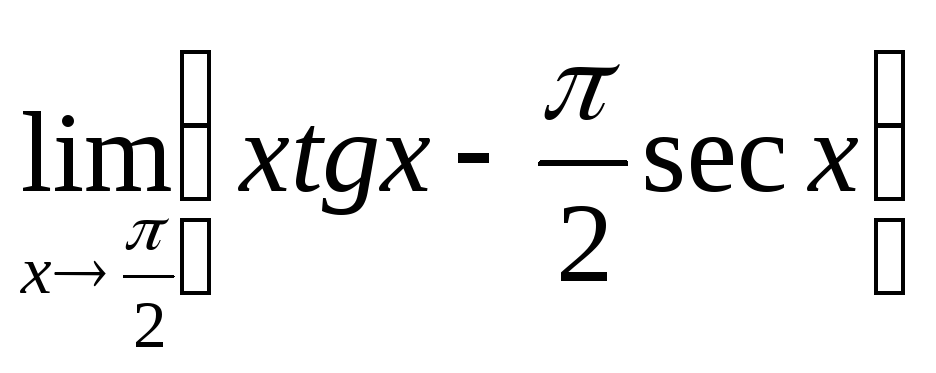