Обчислення площі поверхні тіла обертання
Площа
поверхні, що утворюється при обертанні
навколо осі
кривої
,
обчислюється за формулою
.
3.48.
Обчислити площу поверхні частини
параболоїда обертання
.
3.49.
Обчислити площу поверхні, що утворюється
при обертанні навколо осі
кривої:
1)
;
2)
;
3)
;
4)
;
5)
.
3.50.
Знайти площу сфери радіуса
,
якщо сфера утворюється обертанням
навколо осі
півкола:
,
.
3.51.
Знайти площу поверхні тора, що утворюється
обертанням навколо осі
кола:
.
Застосування визначеного інтеграла у фізиці
3.52.
Знайти координати центра ваги півкола
.
3.53.
Знайти координати центра ваги дуги
лінії
.
3.54.
Знайти координати центра ваги фігури,
обмеженої еліпсом
та осями координат (І чверть).
3.55.
Знайти координати центра ваги фігури,
що обмежена лініями6
.
3.56.
Знайти координати центра ваги параболічного
сегмента, що обмежений лініями:
.
3.57.
Яку роботу необхідно виконати, щоб
відкачати воду, що заповнює вертикальну
цистерну радіуса
та висоти
?
3.58.
Траєкторія руху електрона має в полярних
координатах рівняння
.
Знайти довжину траєкторії електрона,
якщо
.
3.59. Обчислити шлях, що пройшла матеріальна точка за час
від
с
до
с,
якщо швидкість
.
3.60.
Яку роботу необхідно виконати, що
підняти ракету масою
з поверхні Землі на висоту
,
якщо сила земного тяжіння
,
де -
середній радіус Землі,
- віддаль ракети від центра Землі.
3.61.
Швидкість точки змінюється за законом
. Знайти шлях, який точка
пройде до зупинки.
3.62.Швидкість тіла, що кинуте вертикально
вгору з початковою швидкістю
,
без врахування опору повітря, дорівнює
,
де
- прискорення вільного падіння. На яку
максимальну висоту підніметься тіло?
3.63.
Точка, що лежить на осі
,
виконує гармонічні коливання навколо
початку координат зі швидкістю
,
де
- час,
- сталі. Знайти закон коливання точки і
середнє значення абсолютної величини
швидкості за період коливань.
3.64.
Два тіла рухаються по одній прямій,
починаючи рух разом з однієї точки.
Швидкість першого
,
другого -
.
В який момент часу та на якій віддалі
від початку руху вони знову будуть
поряд?
3.65.
Електричний заряд
,
що зосереджений в початку координат,
відштовхує заряд
з точки
у точку
.
Обчислити роботу
,
яка виконується.
Невласні інтеграли з нескінченими межами (і роду)
Обчислити невласні інтеграли ( або встановити розбіжність):
3.66.
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
;
;
;
;
;
.3.67.
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
;
;
;
;
;
.3.68.
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
|
7)
|
8)
|
|
;
;
;
;
;
;
.3.69.
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
|
;
;
;
;
;3.70. Дослідити на збіжність невласні інтеграли:
|
1)
|
2)
|
|
3)
|
4)
|
|
5)
|
6)
|
|
7)
|
8)
|
|
9)
|
|
;
;
;
;
;
;
;
;
.
Невласні інтеграли від необмежених функцій (іі роду)
Обчислити невласні інтеграли (або встановити їх розбіжність):
3.71.
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
|
7)
|
8)
|
9)
|
;
;
;
;
;
;
;
;
.3.72.
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
|
7)
|
|
|
;
;
;
;
;
;
.3.73.
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
;
;
;
;
;
.
Відповіді
3.6.
1)
;
2)
;
3)
;
4)
;
5)
;
6)
.3.7. 1)
;
2)
;3)
;
4)
;
5)
;
6)
.3.8.
;
2)
;
3)
;
4)
;
5)
;
6)
.3.9. 1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
.3.10. 1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
.3.11. 1)
;
2)
;
3)
;
4)
;
5)
;
6)
.3.13.
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
.
3.14.
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;3.15. 1)
;
2)
;
7)
;
8)
;
9)
.3.16. 1)
;
2)
;
4)
.3.17. 2)
;
3)
;
4)
;
5)
;
6)
;
9)
.
3.18.1)
;
2)
;
3)
;
4)
;
5)
;
6)
;3.19. 1)
;
2)
;
3)
;
4)
.
3.20.
2)
;
4)
;
7)
;
8)
;
9)
.
3.21.1)
;
2)
;
3)
;
4)
;
5)
;
6)
.3.22. 1)
;
2)
;
3)
;
4)
;
5)
;
6)
.3.24. 1)
;
2)
;
3)
;
4)
;
5)
;
7)
;
8)
.3.25. 1)
;
2)
;
3)
;
4)
;
5)
.3.26. 1)
;
2) 4,5;
3)
5; 4)
;
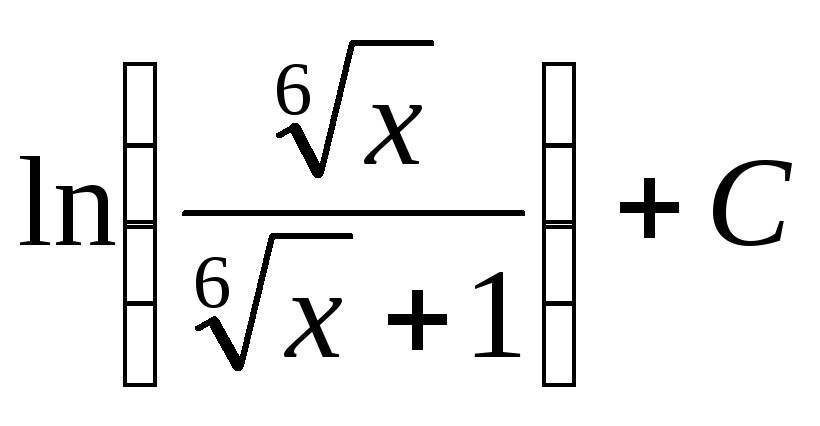5)
;
6) 2,5; 7) 1; 8) 1; 9)
.
3.27.
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7) 0,5; 8)
;
9)
.3.29. Перший.3.30. 36 м.
3.31.
1)
;
2)
.3.33. 1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8) 0,25;
9)
.3.34. 1)
;
;
3)
;
4) 2; 5)
.3.35. 1) 1; 2) 1; 3)
;
4)
;
5)
;
6)
;
7)
.
3.36.
1)
;
2)
;
3)
;
4) 1; 5)
;
6)
.
3.37.
1) 0,25; 2) 0,75; 3)
;
4) 0,5.3.38. 1)
0; 2)
.
3.39.
1)
;
2)
;
3) 9; 4)
;
5)
;
6)
;
7)
.3.40. 1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
.3.41.
;
3.42.1)
;
2)
;
3)
;
4)
.3.43.
.
3.44.
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
.3.45.
1)
;
2)
;
3)
;
4)
;5)
;
6)
;3.46. 1)
;
2)
;
3)
;
4)
.
3.47.
.
3.48.
.
3.49.1)
;
2)
;
3)
;
4)
.3.50.
.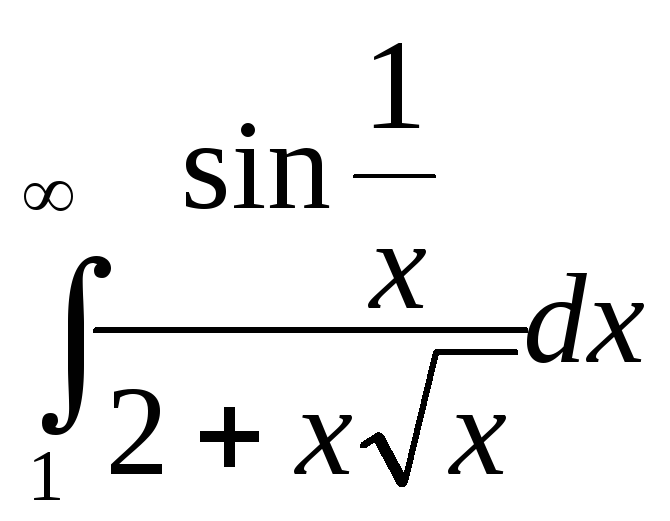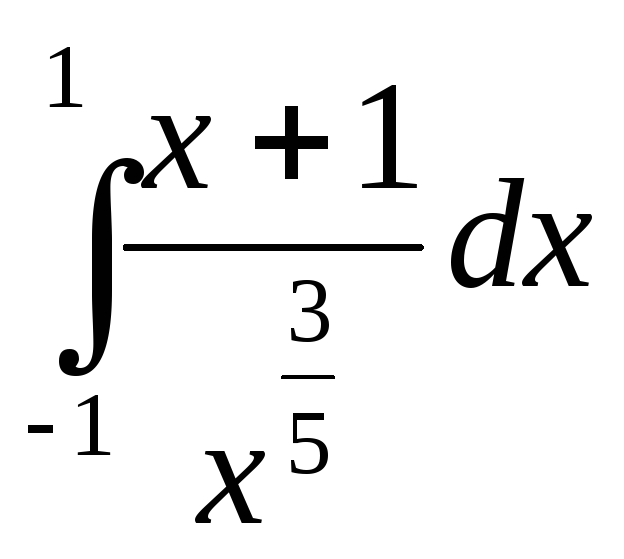