Тема 3.Інтегральне числення функції однієї змінної Невизначений інтеграл
3.1. Перевірити, чи
будуть функції
первісними для функцій
:
1)
,
,
;
2)
,
,
;
3)
,
,
;
4)
,
,
,
;
;
5)
,
,
,
знайти ту первісну, яка при
перетворюється в нуль.
3.2. Знайти інтеграли, застосувавши формулу
,
:
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
;
;
стала);
;
;
.3.3. Знайти інтеграли, застосувавши формулу
,
:
|
1)
|
2)
|
|
3)
|
4)
|
|
5)
|
|
;д3
;
;
;
.3.4. Користуючись таблицею основних інтегралів, знайти наступні інтеграли. Результати перевірити диференціюванням.
|
1)
|
2)
|
|
3)
|
4)
|
|
5)
|
6)
|
;
;
;
;
;
.3.5. Знайти інтеграли, застосувавши основні співвідношення між тригонометричними функціями та формули інтегрування тригонометричних функцій:
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
|
;
;
;
;
.3.6. Перетворенням підінтегральної функції звести до табличних наступні інтеграли і знайти їх:
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
;
;
;
;
;
.
Методом підстановки (заміни змінної або підведенням функції під знак диференціалу) знайти інтеграли:
3.7.
|
1)
|
2)
|
3)
|
|
4) |
5)
|
6)
|
;
;
;
;
;
.3.8.
|
1)
|
2)
|
|
3)
|
4)
|
|
5)
|
6)
|
;
;
;
;
;
.3.9.
|
1)
|
2)
|
|
3)
|
4)
|
|
5)
|
6)
|
|
7)
|
8)
|
;
;
;
;
;
;
.3.10.
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
|
7)
|
8)
|
9)
|
;
;
;
;
;
;
;
;
.3.11. Знайти інтеграли методом підстановки:
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
;
;
;
;
;
. 3.12.
Знайти інтеграли, що мають вигляд
:
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
|
7)
|
|
|
;
;
;
;
;
;
.3.13. Застосувати метод інтегрування частинами:
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
|
7)
|
8)
|
9)
|
;
;
;
;
;
;
;
;
.3.14. Знайти інтеграли:
|
1)
|
2)
|
3)
|
|
4)
|
5) |
6)
|
|
7)
|
8)
|
9) |
|
10) |
|
|
;
;
;
;
;
;
;
;
;
.3.15. Інтегрування функцій, що містять квадратний тричлен:
|
1) |
2) |
3) |
|
4) |
5) |
6) |
|
7) |
8) |
9) |
;
;
;
;
;
;
;
;
.3.16. Знайти інтеграли:
|
1) |
2) |
3) |
|
4) |
5) |
6) |
|
7) |
8) |
|
;
;
;
;
;
;
;
.3.17. Проінтегрувати раціональні дроби:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
.
3.18. Проінтегрувати деякі ірраціональні функції:
|
1)
|
2)
|
|
3)
|
4)
|
|
5)
|
6)
|
|
7)
|
|
;
;
;
;
;
;
.
3.19. Знайти інтеграли,
застосувавши підстановку
:
|
1)
|
2)
|
|
3)
|
4)
|
;
;
;
.3.20. Знайти інтеграли від тригонометричних функцій:
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
|
7)
|
8)
|
9)
|
;
;
;
;
;
;
;
;
.3.21. Знайти інтеграли, застосувавши універсальну тригонометричну підстановку:
|
1)
|
2)
|
|
3)
|
4)
|
|
5)
|
6)
|
;
;
;
;
;
. 3.22.
Знайти інтеграли (підстановка
):
|
1)
|
2)
|
|
3)
|
4)
|
|
5)
|
6)
|
;
;
;
;
;
.3.23. Знайти інтеграли (перейти від добутку тригонометричних функцій до суми):
|
1)
|
2)
|
|
3)
|
4)
|
|
5)
|
6)
|
;
;
;
;
;
.3.24. Використовуючи тригонометричні підстановки, знайти інтеграли:
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
|
7)
|
8)
|
9)
|
;
;
;
;
;
;
;
;
.3.25.Знайти інтеграли:
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
|
;
;
;
;
;
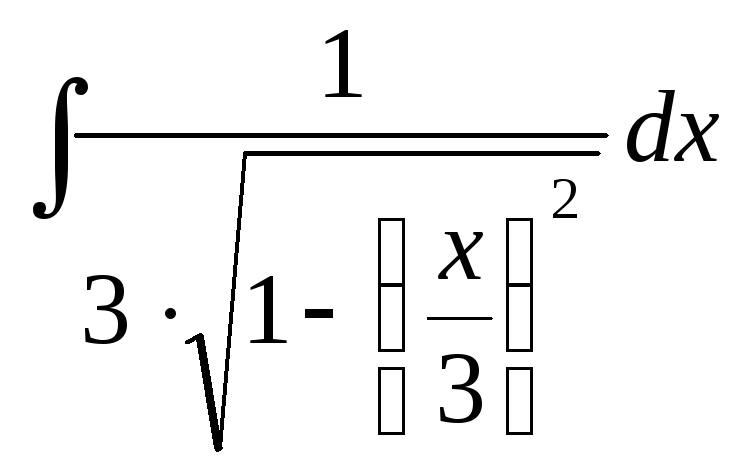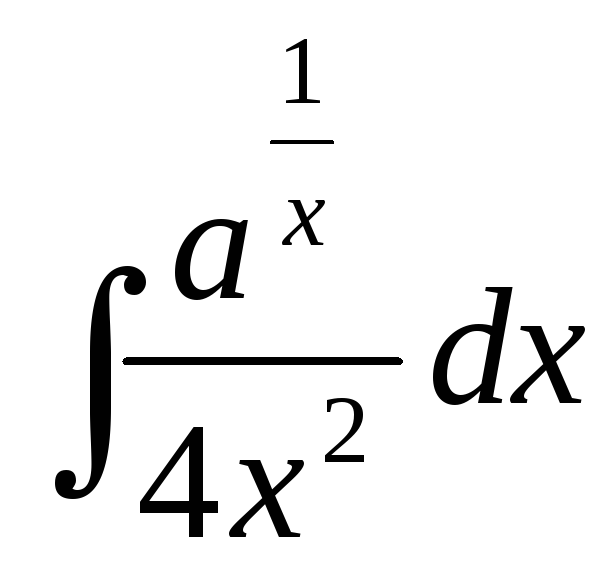