19

Тема 1. Вступ до математичного аналізу Елементи теорії множин та математичної логіки

1.1. Зобразити за допомогою діаграм Ейлера – Венна такі множини:

1) ;	2) ;	3) ;
4) ;	5) ;	6) .

1.2. Довести за допомогою діаграм Ейлера – Венна, що:

1) ;	2) ;
3) ;	4) .
5) ;	6) .

1.3. Нехай універсальною множиною є множина усіх натуральних чисел. Дано множини: А = {1;2;3;4;5}, B = {2;4;6;8},

C = {2;4;6;…}, D = {3;6;9;12;…}.Знайти множини:

1) ;	2) ;	3) ;
4) ;	5) ;	6) .

1.4.

1. Нехай- універсальна множина,. Знайти множини.

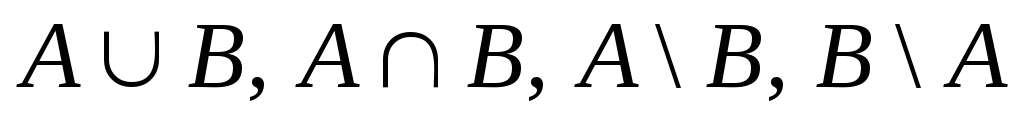2. - множина чисел, що діляться на 3,- множина чисел, не більших 6,- множина парних чисел. Записати:

1) {3,6};	2) {1,3,5,7,…};	3) {9,15,12,18,…};	4){7,8,9,10,…};
5) ;	6) ;	7) ;	8).

1.5. З’ясувати, в якому випадку мають місце співвідношення:

1) ;	2) Ø;	3) ;
4) ;	5) ;	6) .

1.6. Довести:

1) ;

2) ;

3) ; 4).

1.7.

1) Наступні множини зобразити геометрично на числовій прямій:,,

. Чи вірно, щоØ,, ?

2) Дано множину. Записати всі можливі підмножини.

1.8. . Знайти.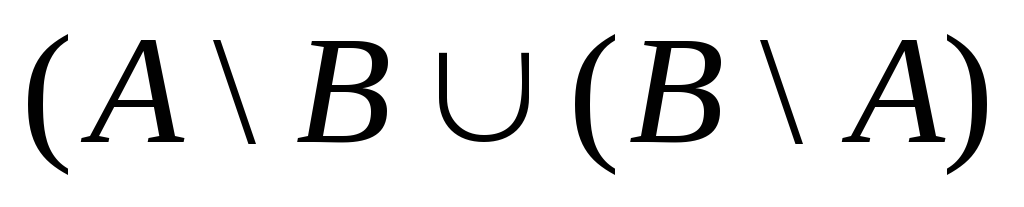

1.9.

1) Зобразити на числовій прямій множини: та знайти:;

;

2) Записати і зобразити наступні множини: ,

,;

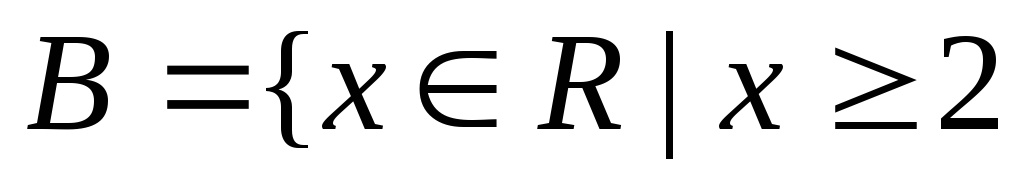3) Дано: , . Записати множини:.

1.10. Нехай . Знайтита.

1.11. Нехай 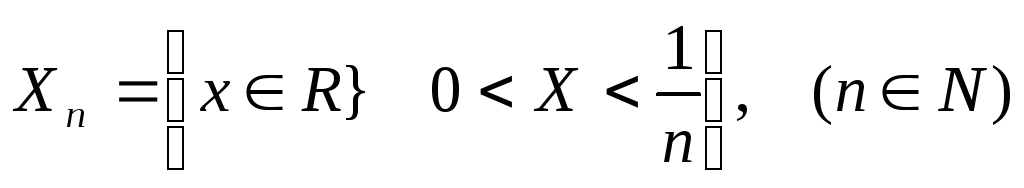. Знайти:

1) ; 2); 3).

1.12. Знайти множини розв’язків рівнянь:

1) ; 2);

3) ; 4); 5);

6) ; 7).

1.13. Навести три приклади квадратних рівнянь, множина

розв’язків яких відповідно: порожня, має лише один корінь (кра-

тний); має два різні дійсні корені.

1.14. Які з наведених речень є висловленнями? Якщо речення є висловленнями, то істинне воно, чи хибне?

1) ; 2); 3)- парне число;

4) Для всіх справедливо:;

5) Трикутник АВС – прямокутник;

6) 18 ділиться на 3; 7) .

1.15. З простих висловлень А та В побудувати висловленняі встановити їх істинність.

1) А: “15 ділиться на 5”, В: “5 < 1”;

2) А: “”, В: “”;

3) А: “Всі кути квадрата прямі”, В: “Діагоналі прямокутника не рівні між собою”;

4) А: “”, В: “8 – просте число”;

5) А: “Гіпотенуза прямокутного трикутника більша за його катет”, В: “”.

1.16. Користуючись формулами , звільнитись від знака імплікації і спростити формули:

1) ;	2) ;
3) ;	4) .

1.17. Скласти таблиці істинності для наступних формул:

1) ; 2); 3).

1.18. Використовуючи таблиці істинності, довести рівносильність наступних формул:

3) ;	4) .
1) ;	2) ;

1.19. Вказати, які з наступних речень є предикатами:

1) ;	2) ;	3) ;
4) ;	5) ;	6)

1.20. Довести, що формули тає водночас або істинними, або хибними (закон контрапозиції).

1.21. Нехай М: “Даний чотирикутник - паралелограм”, К: “ Дві протилежні сторони чотирикутника паралельні”. Чи буде істинною імплікація: 1) ? 2)? 3) Чи можна стверджувати, щоє достатньою умовою для?

1.22. Нехай М: “Дане число ділиться на 9”, К: “Дане число ділиться на 3”. Сформулювати і визначити, чи буде істинним твердження: 1) ; 2).

1.23. Наступні висловлення записати за допомогою символів і встановити істинність чи хибність кожного з них:

1) “Для кожного додатного числа існує таке від’ємне число, для якого”;

2) “Не існує раціонального числа такого, що”;

3) “Для кожного додатного числа існують числа, які більше за.

1.24. Задано предикат : “Ціле числоє дільником числа”. Знайти множину істинності цього предиката, якщо:

1) ; 2); 3).

1.25. Яка властивість функції записується у вигляді формули:

1) ;

2) ;

3) ?

1.26. Наступні висловлення записати за допомогою символів і встановити їх істинність:

1) “Існує таке ціле число , що”;

2) “Для кожного дійсного числа виконується”.
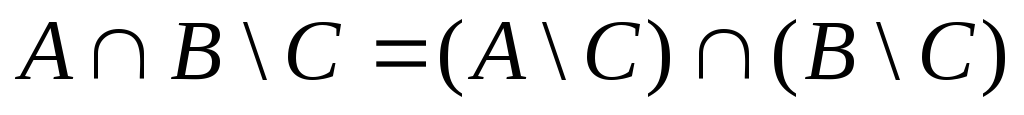