90

Тема 5. ІНТЕГРАЛИ ПО ОБЛАСТІ

Подвійний інтеграл І-го роду

5.1. Поміняти порядок інтегрування:

1)	;	2)	;
3)	;	4)	;
5)	;	6)	;
7)	;	8)	;
9)	;	10)	.

5.2. Подвійні інтеграли записати у вигляді повторних визначених інтегралів (двома способами):

1) , якщо область обмежена прямими

2) , якщо область - трапеція з вершинами ;

3) якщо область обмежена лініями

;

4) якщо область обмежена лініями ;

5) , якщо область обмежена лініями .

5.3. Обчислити , якщо область - прямокутник .

5.4. Обчислити , якщо область - прямокутник .

5.5. Обчислити , якщо область обмежена прямими .

5.6. Обчислити , якщо область обмежена лініями .

5.7. Обчислити , якщо область - трикутник з вершинами .

5.8. Обчислити , якщо область обмежена лініями .

5.9. Обчислити , якщо область обмежена

лініями .

5.10. Обчислити , якщо область обмежена

лініями .

5.11. Знайти середнє значення функції у трикутнику з вершинами .

5.12. Обчислити площу фігури, обмеженої лініями:

1)	;	2)	;
3)	;	4)	;
5)	.

5.13. Знайти масу пластинки, обмеженої лініями , якщо поверхнева густина пластинки .

5.14. Нехай область , обмежена лініями , це крило літака, яке відбиває електромагнітну енергію радіолокаційної станції. Функція – густина електромагнітної енергії, яку відбиває одиниця поверхні крила літака. Знайти всю енергію, відбиту крилом літака, якщо .

5.15. На пластинці, обмеженій лініями , розподілений електричний заряд з поверхневою густиною . Знайти повний заряд пластинки.

5.16. Знайти об’єм тіла, обмеженого поверхнями .

5.17. Знайти об’єм тіла, обмеженого параболоїдом

. В основі цього тіла лежить квадрат, обмежений

в площині прямими .

5.18. Знайти об’єм тіла, обмеженого знизу площиною , зверху – площиною , з боків – циліндричною поверхнею і площиною .

Подвійний інтеграл у полярних координатах

5.19. Перейти до полярних координат і записати подвійні інтеграли у вигляді повторних визначених інтегралів:

1) , якщо область обмежена лінією ;

2) , якщо область обмежена лінією ;

3) , якщо область обмежена півколом

y = і віссю ;

4) , якщо область обмежена лініями ;

5) ;

6) .

5.20. Перейти до полярних координат, замінити подвійний інтеграл однократним .

5.21. Обчислити .

5.22. Обчислити , якщо область обмежена лініями .

5.23. Обчислити , якщо область обмежена колом .

5.24. Обчислити , якщо область обмежена лініями .

5.25 Обчислити , якщо область обмежена лініями .

5.26. Обчислити , якщо область - частина круга радіуса з центром в точці , розміщеного в 1-й чверті.

5.27. Знайти площу області, обмеженої лініями і .

5.28. Знайти площу області, обмеженої лініями .

5.29. Знайти площу області, обмеженої :1) лініями ; 2) еліпсом .

5.30. Знайти масу пластинки, обмеженої лініями якщо поверхнева густина пластинки .

5.31. На пластинці, яка має форму круга , розподілений електричний заряд з поверхневою густиною . Знайти повний заряд пластинки.

5.32. Знайти об’єм тіла, обмеженого параболоїдом і площиною .

5.33. Знайти об’єм тіла, обмеженого циліндром і площинами .

5.34. Знайти об’єм тіла, обмеженого поверхнями .

5.35. Знайти площу області, обмеженої кривою , зображеної на рис. 5.1

Рис. 5.1

Потрійний інтеграл у прямокутних координатах

5.36. Обчислити інтеграли:

1) ;

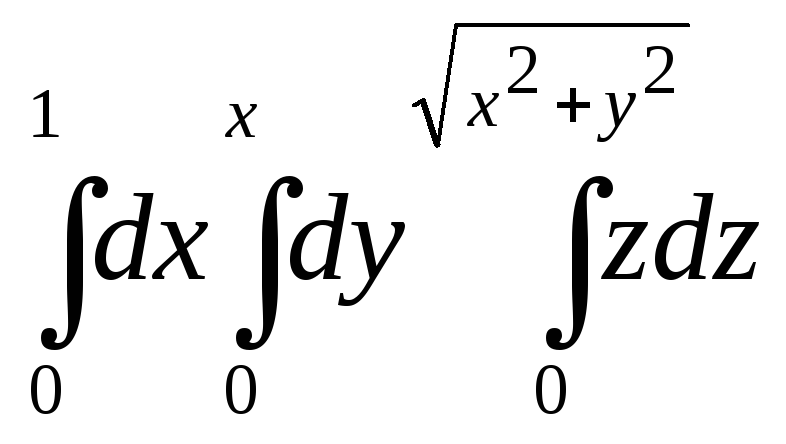2) ;

3) , якщо область обмежена площинами ;

4) , якщо область обмежена площинами ;

5) , якщо область обмежена площинами ;

6) , якщо область обмежена площинами ;

7) , якщо область обмежена площинами ;

8) , якщо область обмежена площинами .

5.37. Знайти масу тіла, обмеженого поверхнями , якщо об’ємна густина .

5.38. У тілі, обмеженому поверхнями , рівномірно розподілений електричний заряд з густиною . Знайти повний заряд тіла.

5.39. У тілі, обмеженому поверхнями , розподілений електричний заряд. Густина заряду в кожній точці пропорційна абсцисі точки. Знайти повний заряд тіла.

5.40. Знайти масу куба , якщо об’ємна густина .

5.41. Знайти об’єм тіла, обмеженого поверхнями .

Потрійний інтеграл у циліндричних і сферичних

координатах

5.42. Обчислити:

1) , якщо область обмежена поверхнями ;

2) , якщо область обмежена поверхнями ;

3) , якщо область обмежена поверхнями ;

4) , якщо область обмежена поверхнями ;

5) , якщо область обмежена поверхнями ;

6) , якщо область обмежена поверхнями ;

5.43. Знайти об’єм тіла, обмеженого поверхнями:

1)		2)
3)		4)
5)		6)
7)		8)
9)		10)

5.44. Знайти масу тіла, обмеженого поверхнями , якщо об’ємна густина .

5.45. Знайти масу тіла, обмеженого поверхнями , якщо об’ємна густина .

5.46. Знайти масу циліндра , обмеженого площинами , якщо об’ємна густина .

5.47. У тілі, обмеженому поверхнями , розподілений електричний заряд з густиною . Знайти повний заряд тіла, де .

5.48. У тілі, обмеженому поверхнями , розподілений електричний заряд. Густина заряду в кожній точці пропорційна квадрату аплікати точки. Знайти повний заряд тіла.

5.49. Знайти масу тіла, обмеженого поверхнями , якщо об’ємна густина .

5.50. Знайти масу тіла, обмеженого поверхнями , якщо об’ємна густина .

5.51. У тілі, обмеженому поверхнями і , розподілений електричний заряд з густиною . Знайти повний заряд тіла.

5.52. Обчислити:

1) , якщо область обмежена поверхнею ;

2) , якщо область обмежена поверхнями ;

3) , якщо область обмежена поверхнями ;

4) , якщо область обмежена поверхнями ;

5) якщо область обмежена поверхнею ;

6) , якщо область обмежена поверхнею ;

5.53. Знайти об’єм тіла, обмеженого поверхнями .

5.54. Знайти масу частини кулі радіуса , яка розміщена в першому октанті, якщо густина в кожній її точці дорівнює відстані цієї точки до площини .

5.55. Знайти масу частини кулі , розміщеної в 1-му октанті, якщо об’ємна густина .

5.56. Знайти об’єм місткості для зберігання окислювача в геодезичній ракеті, якщо місткість обмежена поверхнями .

5.57. Знайти масу тіла, обмеженого поверхнями , якщо об’ємна густина .

5.58. Знайти масу тіла, обмеженого поверхнями , якщо об’ємна густина .

Відповіді

5.3. 1. 5.4. 8. 5.5. . 5.6. . 5.7. . 5.8. . 5.9. .

5.10. . 5.11. . 5.12. 1) ; 2) ; 3) ; 4) 2; 5) .

5.13. . 5.14. 128. 5.15. 2. 5.16. . 5.17. . 5.18. .

5.20. . 5.21. . 5.22. . 5.23. .

5.24. 3. 5.25. . 5.26. . 5.27. . 5.28. . 5.29. 1) ; 2) . 5.30. . 5.31. 3. 5.32. . 5.33. . 5.34. . 5.35. . 5.36. 1) ; 2) ;

3) ; 4) ; 5) ; 6) ; 7) 11; 8) . 5.37..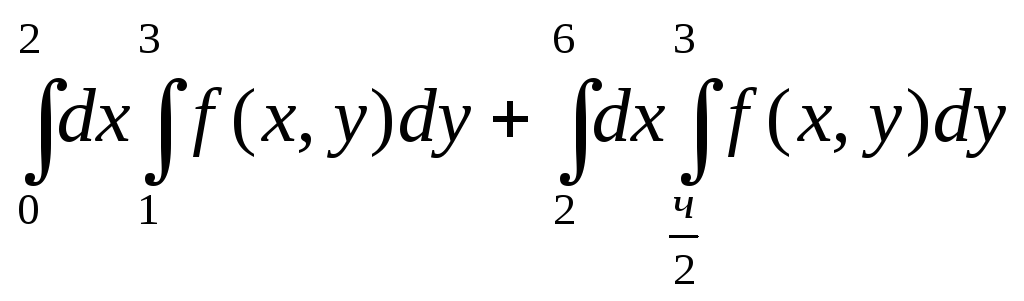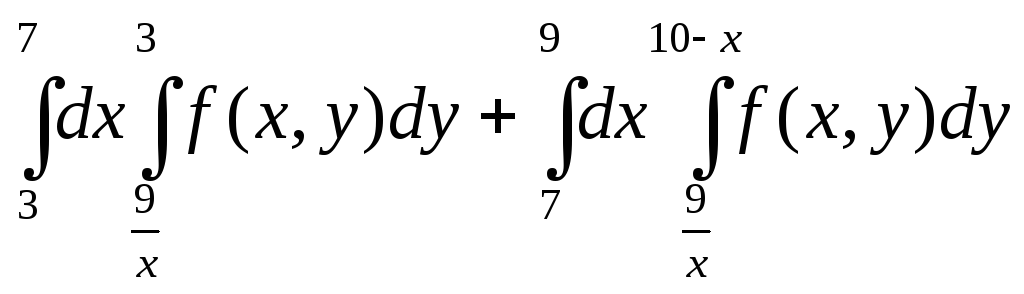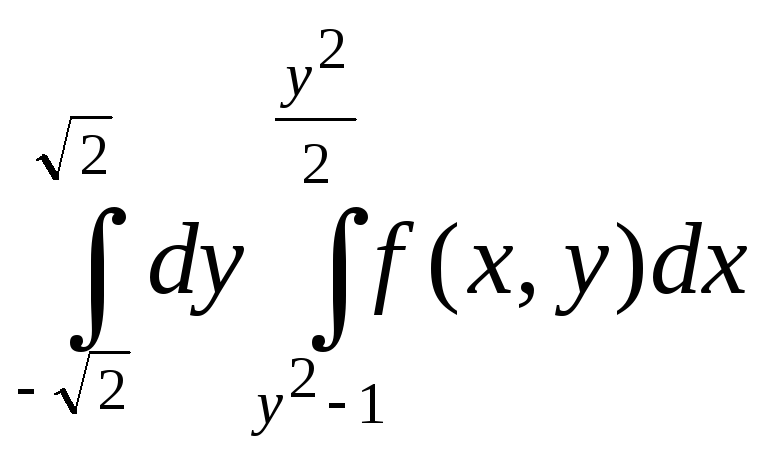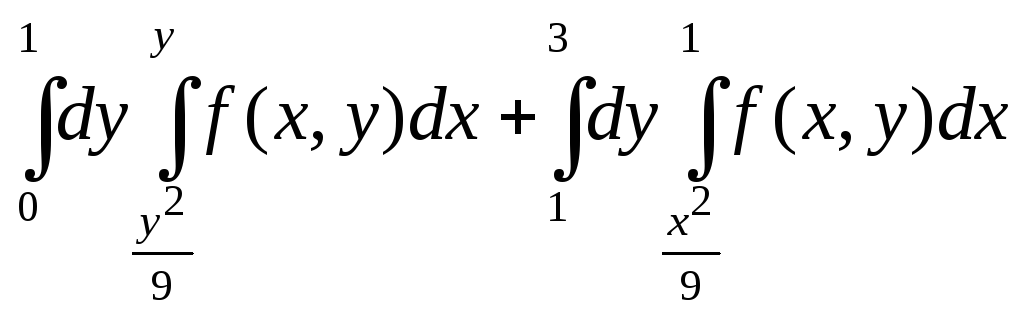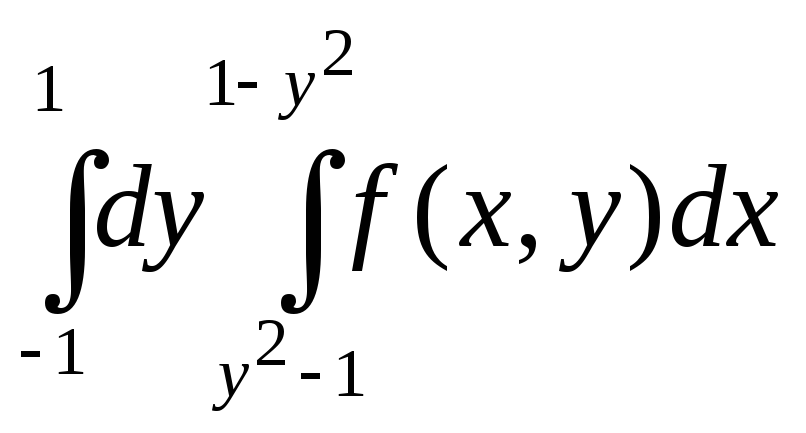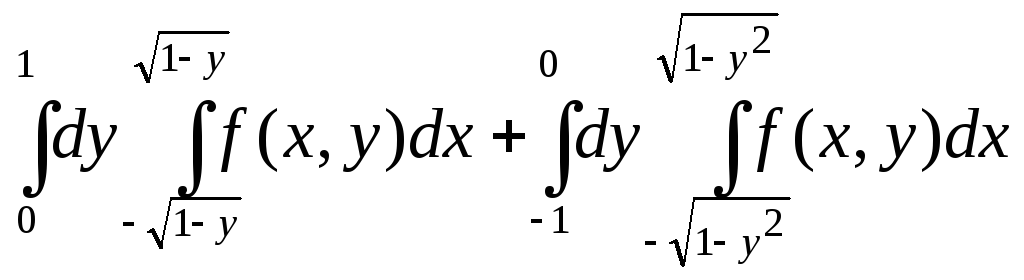