43.Екстремуми функції , необхідні умови

Точка Хо називається точкою локального максимуму(мінімуму) функції y=f(x), якщо існує такий окіл цієї точки U(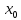), що

Точки максимуму та мінімуму функції називаються точками екстремуму.

Необхідна умова екстремуму :

В точках, підозрілих на екстремум похідна функції f ’(x) дорівнює 0 або не існує.

Точки в яких похідна не існує або дорівнює 0 називають критичними.

Точки в яких похідна рівна 0 називають стаціонарними.

Достатні умови екстремуму:

1)якщо функція f(x) неперервна в околі U() і при переході через точку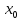її похідна,f ‘(x)змінює знак тобто

для хв межах околуU(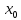) I

Для x в межах околу U(), тоє точкою локального максимуму(мінімуму функціїf(x)

44.Достатні умови екстремуму , перше правило.

Нехай а є критична точка функції , яка в цій точці є неперервною, і нехай існує окіл точки, в якому має похідну , крім, можливо, точка а. Тоді:

1) якщо в інтервалі похідна, а в інтерваліпохідна, то а є точкою максимуму функції ;

2) якщо в інтервалі , а в інтерваліто а є точкою мінімуму функції ; 3) якщо в обох інтервалах іпохіднамає той самий знак ( набуває або тільки додатних, або тільки від’ємних значень), тоне є екстремальною точкою функції.

Перше правило дослідження функції на екстремум. Щоб дослідити функцію на екстремум, треба: 1) знайти стаціонарні точки даної функції (для цього слід розв’язати рівняння , причому з його коренів вибрати тільки дійсні і ті, які є внутрішніми точками області існування функції). 2) знайти точки, в яких похідна не існує (функціяв цих точках існує); 3) у кожній критичній точці перевірити зміну знака похідної першого порядку.

            Теорема. Нехай точка є стаціонарною для функціїі нехай в цій точці існує похідна другого порядку, яка не

дорівнює нулю, . Тоді, якщотоє точкою

мінімуму; якщо , - точкою максимуму функції.

            Друге правило дослідження функції на екстремум. Щоб дослідити функцію на екстремум, треба знайти: 1) стаціонарні точки заданої функції 2) похідну другого порядку в стаціонарній точці. 3) якщо то в цій точці функція має максимум, якщо

мінімум.

47.Випуклі функції. Умова випуклості.Точки перегину.

Опукла функція — функція, яка визначена на опуклій множині лінійного простору, і задовольняє нерівності при всіх λ з проміжку [0, 1]. Нехай область визначення опуклої функції f(x) лежить в скінченовимірному просторі, тоді f(x) неперервна в будь якій внутрішній точці цієї області. Властивості опуклих функцій Нехай x₁, ..., x_m — будь які точки із області визначення опуклої функції f(x), λ₁, ..., λ_m — невід'ємні числа, які в сумі дорівнюють 1. Тоді

.

Якщо f(x) — двічі неперервно-диференційована опукла функція, то матриця її других похідних невід'ємно визначена.

Угнута функція або увігнута функція — протилежність до опуклої функції. До угнутих функцій належать неперервні функції з від'ємною другою похідною. Довільна неперервна фукнція не обов'язково або опукла, або угнута, але вона може бути опуклою або угнутою на певних інтервалах, розділених точками перегину. Дійсна функція f визначена на інтервалі (або на будь-якій опуклій множині C деякого векторного простору) називається угнутою, якщо для будь-яких двох точок x і y в її області визначення C і будь-якого t в [0,1], маємо

Функція називається строго угнутою, якщо

для будь-якого t в (0,1) і x ≠ y.

Для функції f:R→R, це означення просто стверджує, що для кожного z між x і y, точки (z, f(z)) на графіку f є вище прямої, що з'єднує точки (x, f(x)) і (y, f(y)). Функція f(x) є квазіугнутою, якщо множини верхнього контура функції є