36 Формула Тейлора для многочленів та довільних функцій

Теорема (Тейлора, 1685-1731, Англія) Нехай функція в околі точки має похідні до -го порядку включно. Якщо з вказаного околу, то існує точка з цього околу, для якої має місце формула

де      .

Ця формула називається формулою Тейлора, - залишковий член.

Доведення. Позначимо

Многочлен називається многочленом Тейлора функціїв околі точки.

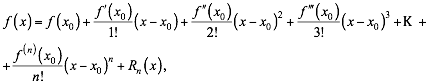
Тоді залишковий член .

Отже, нам потрібно довести, що залишковий член виражається вказаною формулою.

Нехай . Для довільногорозглянемо функцію

   і   .

Отже, задовольняє умові теореми Ролля на. Знайдемо похідну функції:

або             .

За теоремою Ролля існує така, що, тобто

 

або             .

Саме цю формулу залишкового члена найчастіше використовують. Залишковий член у вказаній формі називається залишковим членом у формі Лагранжа. Оскільки , то залишковий членможна записати у вигляді

.

Зустрічаються і інші форми залишкового члена формули Тейлора.

Якщо , то залишковий членбуде нескінченно малою вищого порядку порівняно з, тобтопри. Такий запис залишкового членаформули Тейлора називають зображенням залишкового члена у формі Пеано.

Наслідок. Для довільного алгебраїчний многочлен степеняможе бути записаний у вигляді

При формула Тейлора набуде вигляду

де і називається формулою Маклорена з залишковим членом у формі Пеано, вона має вигляд

, .

Формула Тейлора використовується при доведенні багатьох теорем у диференціальному численні. Якщо говорити нестрого, то формула Тейлора показує поведінку функції в околі деякої точки.

Теорема:

Нехай функція маєпохідну в деякому околі точки , 

Нехай 

Нехай — довільне додатнє число

тоді: приабопри:

Це формула Тейлора із залишковим членом у загальній формі.

39.Застосування формули Тейлора до наближених обчислень.

40. Правило Лопіталя- Бернуллі. Розкриття невизначеності 0/0 та ∞/∞ .

Пра́вило Лопіта́ля — у математичному аналізі — метод знаходження границь функції, розкриття невизначеностей вигляду і. Теорема, що обґрунтовує метод, стверджує що за деяких умов границя відчастки функцій дорівнює границі частки їхніх похідних. Правило говорить, що якщо функції ізадовольняють такі умови:

або ;

;

в проколотому околі ;

Якщо і— диференційовані в проколотому околі,

то існує . При цьому теорема вірна і для інших баз. Доведемо теорему для випадку, коли границі функцій дорівнюють нулю (т.з. невизначеність вигляду ). Оскільки ми розглядаємо функції ілише у правому проколотому півоколі точки, ми можемо неперервним чином їх довизначити в цій точці: нехай. Візьмемо деякийз даного півоколу і застосуємо до відрізкутеорему Коші. За цією теоремою отримаємо:

але , тому

Далі, записавши визначення границі функції відношення похідних і позначивши останню через , з отриманої рівності виводимо:

для скінченної границі і

для нескінченої,

що є визначенням границі відношення функцій.

Відношення нескінченно великих

Доведемо теорему для невизначеностей вигляду .

Нехай, для початку, границя відношення похідних скінченна і рівна . Тоді, при прямуваннідосправа, це відношення можна записати як, де—O.

Запишемо цю умову:

.

Зафіксуємо з відрізкаі застосуємотеорему Коші до всіх з відрізка:

, що можна привести до такого вигляду:

.

Для , достатньо близьких до, вираз має межу першого множника правої частини рівний одиниці (так які—константи, а іпрямують до безмежності). Значить, цей множник рівний, де— нескінченно мала функція при прямуваннідосправа. Випишемо визначення цього факту, використовуючи те ж значення, що і в визначенні для:

.

Отримали, що відношення функцій можна подати у вигляді , і. По будь-якому данномуможна знайти таке, щоб модуль різниці відношення функцій ібув менше, значить, границя відношення функцій дійсно рівна.