Вакарчук І.О. Квантова механіка

Шрединґера. Таким чином, дописуючи iндекси, що нумерують стани, маємо хвильову функцiю, яка описує стацiонарнi стани з певною енерґiєю En:

ψn(q, t) = e−iEnt/~ψn(q),

ˆ

Hψn(q) = Enψn(q).

Система функцiй ψn(q, t) є повною, i будь-яка функцiя

X

ψ(q, t) = Cne−iEnt/~ψn(q),

n

а величина |Cn|2 дорiвнює, згiдно з принципом суперпозицiї, iмо-

вiрностi рiзних значень енерґiї.

Зробимо тепер кiлька зауважень. Для дискретних станiв iснує

iнтеґрал

Z Z

|ψn(q, t)|2dq = |ψn(q)|2dq = 1

це означає, що ψn(q) достатньо швидко спадає на безмежностi.

Iншими словами, iмовiрнiсть перебування частинки на безмежностi є зникаюче малою частинка рухається в обмеженому об’ємi. Висновок: якщо частинка рухається в обмеженiй дiлянцi простору (фiнiтний рух), то її рiвнi енерґiї дискретнi, вони квантуються. Навпаки, у випадку неперервного спектра хвильовi функцiї нормуються на δ-функцiю й iнтеґрал не iснує: R |ψE (q)|2dq = ∞. Це означає, що ψE (q) слабо спадає на безмежностi або взагалi не спа-

дає, i, таким чином, iмовiрнiсть знайти частинку на безмежностi вiдмiнна вiд нуля. Отже, якщо частинка рухається в необмеженiй дiлянцi (iнфiнiтний рух), то енерґетичний спектр є неперервним.

Стацiонарним станом, як показує досвiд, фактично є лише основний стан атомної системи, решта квазiстацiонарнi. У збудженому станi атом перебуває лише деякий час, а згодом вiн спонтанно переходить на нижнiй рiвень, випромiнюючи кванти енерґiї. Причиною спонтанного випромiнювання свiтла є взаємодiя електронiв атома з нульовими коливаннями електромагнiтного поля. Хоча середнi значення напруженостей поля у вакуумному станi дорiвнюють нулевi, середнi квадратичнi вiдхилення, унаслiдок принципу невизначеностей, вiдмiннi вiд нуля.

171

Тут ми торкаємось питання необоротностi фiзичних подiй у часi. Рiвняння Шрединґера є оборотним у часi: замiна t на (−t) та ψ на ψ залишає його незмiнним. Отже, воно не може опи-

сувати квазiстацiонарних станiв, якщо їх не “заносити в теорiю руками”. Внесення необоротностi означає, що вiдбирається лише певний клас розв’язкiв рiвняння Шрединґера для системи “атоми плюс поле”. При такому вiдборi розв’язкiв неявно припускається, що випромiнений фотон, блукаючи Всесвiтом, бiльше нiколи не зустрiне атома i не переведе його знову в збуджений стан.

Розв’язування стацiонарного рiвняння Шрединґера це одна iз центральних задач квантової механiки, оскiльки власнi значення енерґiї En квантовомеханiчних систем, або, як кажуть, їхнiй

енерґетичний спектр, є найважливiшою фiзичною характеристикою, яка визначає низку iнших властивостей, а хвильовi функцiї ψn(q) дозволяють розраховувати не лише середнi значення спо-

стережуваних величин, а й просторову структуру атомiв та їх сукупностей, iмовiрностi переходiв мiж станами, зокрема iнтенсивностi випромiнювання й поглинання свiтла та перерiзи розсiяння одних частинок на iнших. Фактично бiльша частина нашого курсу присвячена знаходженню розв’язкiв рiвняння Шрединґера для рiзноманiтних задач. Зрозумiло, що не для всiх потенцiалiв це рiвняння допускає точний аналiтичний розв’язок. З кiлькома такими задачами, що мають точний розв’язок, ми ознайомимось у наступних роздiлах. Для iнших задач розвинемо наближенi методи, такi, як теорiя збурень та варiацiйний принцип.

На рiвняння Шрединґера можна дивитись i по-iншому. А саме, воно дає змогу за вiдомою хвильовою функцiєю знаходити потенцiальну енерґiю. Така постановка питання у класичнiй механiцi вiдповiдає обчисленню сили чи потенцiалу за вiдомою траєкторiєю частинки (формула Бiне).

Розгляньмо, наприклад, рух частинки в одновимiрному просторi з координатою x у силовому полi з потенцiальною енерґiєю U = U(x). Вiзьмiмо до уваги основний стан. Нагадаємо, що стан з

найнижчим значенням енерґiї називають основним станом. Як ми знаємо, основний стан є невиродженим i його хвильова функцiя не має вузлiв (див. §10). У зв’язку з цим, хвильову функцiю основного стану ψ = ψ(x) завжди можна вибрати дiйсною i додатною,

тому записуємо її так:

ψ = ceu,

172

c стала нормування, а для функцiї u = u(x) знаходимо

рiвняння, яке випливає зi стацiонарного рiвняння Шрединґера

− ~2 ψ′′ + Uψ = Eψ,

2m

E енерґiя основного стану, а штрих означає похiдну за координатою x. Отже, для u маємо таке рiвняння:

− ~2 [u′′ + (u′)2] + U = E. 2m

Оскiльки функцiя u за умовою задана, то звiдси й знаходимо по-

тенцiальну енерґiю.

Наприклад, якщо u = −ax2, a > 0, то наше рiвняння є таким:

~2 (a − 2a2x2) + U = E, m

звiдси

E = ~2 a, m

а потенцiальна енерґiя

U = 2~2a2 x2. m

Тобто виявляється, що U є потенцiальною енерґiєю лiнiйного гармонiчного осцилятора iз частотою ω = 2~a/m. Отже, записана через частоту повна енерґiя E = ~ω/2, а з умови нормування знаходимо сталу c:

Z∞

|c|2 e−2ax2 dx = 1,

−∞

iнтеґрал дорiвнює pπ/2a i c = (mω/π~)1/4.

Вiзьмiмо складнiшу функцiю

u= −ax2 − bx4

i з рiвняння для неї маємо

~2

E = m a,

173

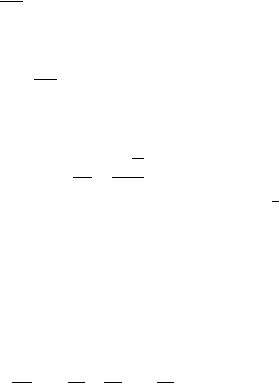
U = 2~2 4b2x6 + 4abx4 + (a2 − 3b)x2 . m

Цей результат можна трактувати ще й так: для потенцiальної енерґiї

U = 2~2 Ax6 + Bx4 + Cx2 m

рiвняння Шрединґера допускає точний аналiтичний розв’язок за умови, що A = 4b2, B = 4ab, а C = a2 − 3b, тобто за умови, що коефiцiєнт C вже не є довiльним, а

√

C = B2 − 3 A.

4A 2

√

Якщо C = 0, то точний розв’язок маємо за умови, що B = 6A3/4.

Дослiджуваний потенцiал має один точний розв’язок. Зауважимо, що потенцiали, для яких вiдомо кiлька точних розв’язкiв (для основного i збуджених станiв), мають назву “квазiточнорозв’язуванi”.

Приклад. Довести, що середнє значення вiд похiдної гамiльтонiана ˆ за

H

деяким параметром λ дорiвнює похiднiй енерґiї E за λ.

Нехай гамiльтонiан системи ˆ , а отже, i його власнi значення, i власнi

H

функцiї залежать вiд деякого параметра λ. Продиференцiюймо рiвняння на

Помножмо це рiвняння злiва на ψ i проiнтеґруймо за змiнними q:

Користуючись самоспряженiстю оператора ˆ , “перекидаємо” його дiю в дру-

H

гому доданку злiва на ψ . У результатi цей доданок скорочується з другим

доданком у правiй частинi рiвняння. Отже, ми отримуємо остаточно, що

*+

Цей результат справедливий, очевидно, для будь-якого ермiтового оператора. Вiн вiдомий як теорема про те, що середнє значення вiд похiдної ермiтового оператора за параметром λ дорiвнює похiднiй вiд середнього значення цього оператора за λ. Помiчаємо, що ця теорема нагадує результат, який ми одержа-

ли для швидкостi змiни середнiх значень операторiв iз часом. У цьому нiчого

174

дивного немає, оскiльки час t в нерелятивiстськiй теорiї є параметром, а не

змiнною.

Для iлюстрацiї можливостей цiєї теореми розгляньмо гамiльтонiан

Якщо в ролi параметра λ узяти масу частинки m, то отримуємо

dE = − p2 . dm 2m2

Тобто середнє значення кiнетичної енерґiї частинки знаходимо простим диференцiюванням повної енерґiї:

pˆ2 = −m dE . 2m dm

Цiкаве спiввiдношення можна одержати, якщо зробити замiну змiнних r = λr′, у результатi якої

оператор pˆ′ канонiчно спряжений до r′. Тепер маємо:

∂E = − 2 pˆ′2 + 1 h(r′ ′)U(λr′)i

∂λ λ3 2m λ

або, повертаючись у правiй частинi до нештрихованих змiнних, отримуємо

∂E = − 2 pˆ2 + 1 h(r )U(r)i. ∂λ λ 2m λ

Оскiльки енерґiя не залежить вiд змiни масштабу довжини, тобто вiд параметра λ, ∂E/∂λ = 0, то ми отримуємо рiвняння

pˆ2

2 = h(r )U(r)i. 2m

Величину, яка стоїть в правiй частинi цього рiвняння, називають вiрiалом сил. Цей вираз є узагальненням на квантовий випадок вiдомої теореми вiрiалу Р. Ю. Е. Клаузiуса (1870 р.).

175

§ 19. Представлення Шрединґера i представлення

Гайзенберґа

Розглянемо хвильове рiвняння, яке описує еволюцiю стану в часi

Еволюцiю в часi можна розглядати як дiю деякого оператора ˆ

S

на хвильову функцiю, задану в певний початковий момент часу, який ми виберемо рiвним нулевi, t = 0:

ψ(q) = ψ(q, t = 0).

З рiвняння Шрединґера дiстаємо рiвняння для оператора еволюцiї

тобто вiн мусить зберiгати норму хвильової функцiї з часом, iншими словами: частинка десь знаходиться в просторi змiни q в довiльний момент часу t.

176

Отже, оператор еволюцiї повинен бути унiтарним:

Такий спосiб опису часової еволюцiї квантової системи, коли хвильовi функцiї залежать вiд часу, називають представленням Шрединґера. Вiдзначимо, що термiн “представлення”, який iсторично утвердив себе, насправдi тут є недоречним мова йде саме про спосiб опису. Тому про такий опис еволюцiї говорять ще як про “картину Шрединґера”.

Можна будувати квантову механiку i так, щоб усю залежнiсть вiд часу перенести на оператори, а хвильовi функцiї в такому представленнi не будуть залежати вiд часу. Такий опис називають зображенням, або “картиною Гайзенберґа”.

177

Отже, будемо вважати, що хвильовi функцiї ψ = ψ(q) не зале-

жать вiд часу. Очевидно, що

ˆ−1 ˆ+

ψ(q) = S ψ(q, t) = S ψ(q, t).

Для знаходження залежностi вiд часу операторiв обчислюємо середнє:

Отже, можемо розраховувати середнi значення за хвильовими

функцiями, незалежними вiд часу. Однак тепер оператор ˆ за-

A

лежить вiд часу i має вигляд:

представлення Гайзенберґа. Приймаючи, що ˆ не залежить яв-

A

но вiд часу, вiзьмемо похiдну за t:

це рiвняння руху для операторiв у представленнi Гайзенберґа. Обчислимо матричнi елементи оператора у представленнi Гай-

178

Отже,

Amn(t) = eiωmntAmn,

де частота переходу ωmn = (Em − En)/~, а похiдна за часом, яку

ми позначимо крапкою,

˙

Amn(t) = iωmnAmn(t).

Цi матрицi вводив Гайзенберґ при побудовi матричної квантової механiки, не знаючи й не вводячи поняття оператора.

Зупинимось ще на одному промiжному способi опису еволюцiї квантових систем у часi так званому представленнi взаємодiї. Представлення взаємодiї здiйснюється оператором еволюцiї, у якому є лише частина повного гамiльтонiана

Оператор еволюцiї, що творить представлення взаємодiї

У цьому представленнi не вся часова залежнiсть переведена з хвильової функцiї на оператори: i оператори, i хвильовi функцiї залежать вiд часу:

179