2. Подання формул алгебри висловлювань у вигляді досконалої нормальної диз’юнктивної або кон’юнктивні форми.

Введемо позначення:

звідси тобто _,

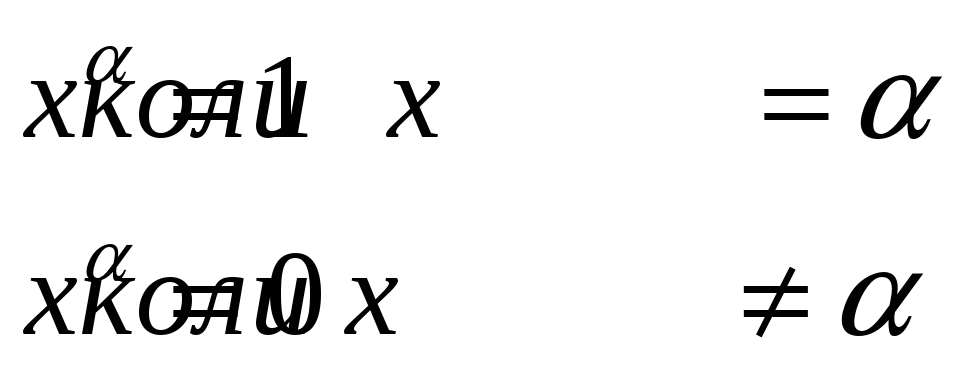- це є диз’юнкція все можливих наборів формули , де формула Н залежить від змінних x₁, x₂, ..., x_n, а пробігає всі можливі набори значень 0 та 1.

Лема: Кожну формулу алгебри висловлювань можна подати в наступному вигляді:

Теорема: Кожна формула алгебри висловлювань, яка не є тотожньо хибною, має єдину (з точністю до перестановок кон’юнктивних одночленів) досконалу диз’юнктивну нормальну форму.

Лема: Будь-яку формулу алгебри висловлювань можна подати у вигляді:

_,

Теорема: Кожна формула алгебри висловлювань, яка не є тавтологією, має єдину (включно до перестановок) досконалу кон’юнктивну нормальну форму.

3.Булеві функції від n аргументів. Вираження булевих функцій через кон’юнкцію, диз’юнкцію і заперечення.

Булевою функцією від одного аргументу називається функція, яка задана на множині двох елементів і приймає значення цій же множині двох елементів (елементи 0 і 1).

х	f1	f2	f3	f4
0	0	0	1	1
1	0	1	0	1

Булевою функцією від двох аргументів називається функція, яка задана на множині і приймає значення на множині .

		0		→’	x	←’	y			↓	↔	y’	←	x’	→	|	1
x	y	g0	g1	g2	g3	g4	g5	g6	g7	g8	g9	g10	g11	g12	g013	g14	g15
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

g₀ – функція тотожньо нуль.

g₁ – кон’юнкція.

g₂ – заперечення імплікації.

g₃ – функція, що приймає значення першого аргументу.

g₄ – заперечення антиімплікації.

g₅ – функція, яка приймає значення другої змінної.

g₆ – сумування за модулем 2.

g₇ – диз’юнкція.

g₈ – стрілка Персона.

g₉ – еквівалентність.

g₁₀ – заперечення другого аргументу.

g₁₁ – антиімплікація.

g₁₂ – заперечення першого аргументу.

g₁₃ – імплікація.

g₁₄ – штрих Шеффера.

g₁₅ – тотожньо одиниця.

Для булевих функцій характерні наступні закони: закон ідемпотентності, комутативності, асоціативності, дистрибутивності, закон поглинання і закон де Моргана.

Деякі додаткові тотожності:

_,,,

Булевою функцією від n аргументів називається функція, яка задана на множині і приймає значення на множині .

Булеві функції називаються рівними, якщо при будь-якому наборі , які підставляються замість функції отримують однакові значення, тобто .

Супер позицією булевих функцій у булевій функції називається така функція, яка отримана у процесі підстановки у функцію f замість змінних функції відповідно, тобто отримується функція .

Отримана функція залежить від аргументів.

Теорема: Кількість різних булевих функцій від n аргументів дорівнює .

Лема: Для будь-якої булевої функції справедливі наступні формули, які ще називають формулами розкладу по змінній x.