Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тернопольский национальный педагогический университет им. В. Гнатюка

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ТЕСТИ_ЗНО_МАТЕМ

.pdf

Скачиваний:

4520

Добавлен:

14.02.2016

Размер:

2.86 Mб

Скачать

☆

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 1819 / 3419 20 21 22 23 24 25 26 27 28 29 30 31 > Следующая >>>

ТЕМА 25. ЗАСТОСУВАННЯ ПОХІДНОЇ ДЛЯ ДОСЛІДЖЕННЯ ФУНКЦІЙ

Завдання 25.1–25.28 мають по п’ять варіантів відповідей, з яких тільки ОДНА ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь.

25.1.Визначити проміжок зростання функції у = х2 – 1.

(–∞; +∞)

[0; +∞)

[1; +∞)

(–∞; –1)

(–∞; 0]

25.2. Знайти проміжки зростання функції y = f(x), якщо f′(x) = (x – 1)(x – 5).

(–∞; –5] [1; +∞)

[–5; –1]

[1; –5]

(–∞; 1] [5; +∞)

(–∞; –5]

25.3. Знайти проміжки спадання функції y = ϕ(x), якщо ϕ′(x) = (x + 2)(х – 1)2(x – 3).

[–3; 2]

(–∞; –3] і [–1; 2]

(–∞; –2] і [1; 3]

(–∞; –2] і [3; +∞)

[–2; 3]

25.4. Знайти проміжки зростання функції y = x2ex .

(–∞; +∞)

(–∞; –2] і [0; +∞)

[–2; 0]

(–∞; 0] і [2; +∞)

[0; 2]

25.5.

Знайти проміжки

спадання функції y = sin2x.

[π + 2πn; 2π + 2πn],

+ πn; π + πn ,

+ 2πn; π + 2πn ,

πn;

+ πn ,

(–∞; +∞)

n Z

25.6. Серед наведених функцій вибрати ту, яка є зростаючою на множині дійсних чисел.

y = –x7

y = cos2x

y = ln(x2 + 1)

y = ex3

y = e

25.7. Серед наведених функцій вибрати ту, в якої проміжком спадання є проміжок [0; +∞).

y =

y = xex

y = ln(x3 + 1)

y = e

+ 1

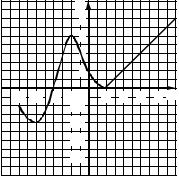
25.8. Скільки критичних точок має функція y = f(x), зображена на рисунку?
y
4
3
2
1
–4 –3 –2 –1 0	1	2	3	4	x
–1
–2
–3
–4

А	Б	В	Г	Д

Одну	дві	три	чотири	більше, ніж чотири

181

25.9. Знайти критичні точки функції

f (x) =

− x2 − 3x .

–3 і –1

–3 і 1

1 і 3

–1 і 3

25.10.

Вказати критичні

точки функції y = x(x – 4)3.

0; 4

1; 4

25.11.

Знайти критичну точку функції у = 2х2 – 4х.

–1

25.12. Знайти критичні точки функції y =

x 2

–2; 2; 0

–2; 2

2; 0

25.13.

Визначити точку

екстремуму функції

у = 2х2 – х + 7.

0,25

–2

25.14. Знайти точки максимуму функції y = f(x), якщо f′(x) = x(x + 3)(x – 5).

–3 і 5

–3

0 і 5

25.15. Знайти точки мінімуму функції y = f(x), якщо f′(x) = x(x – 2)2(x – 5).

0 і 5

0 і 2

25.16.Визначити усі критичні точки функції y = f(x) на відрізку [–4; 4], якщо на рисунку зображено графік функції y = f′(x).

y
4
3
2
1
–4 –3 –2 –1 0	1	2	3	4	x
–1
–2
–3
–4

А	Б	В	Г	Д

–3; –1 і 1	–3 і –1	–2 і 1	–4 і 4	–3 і 1

182

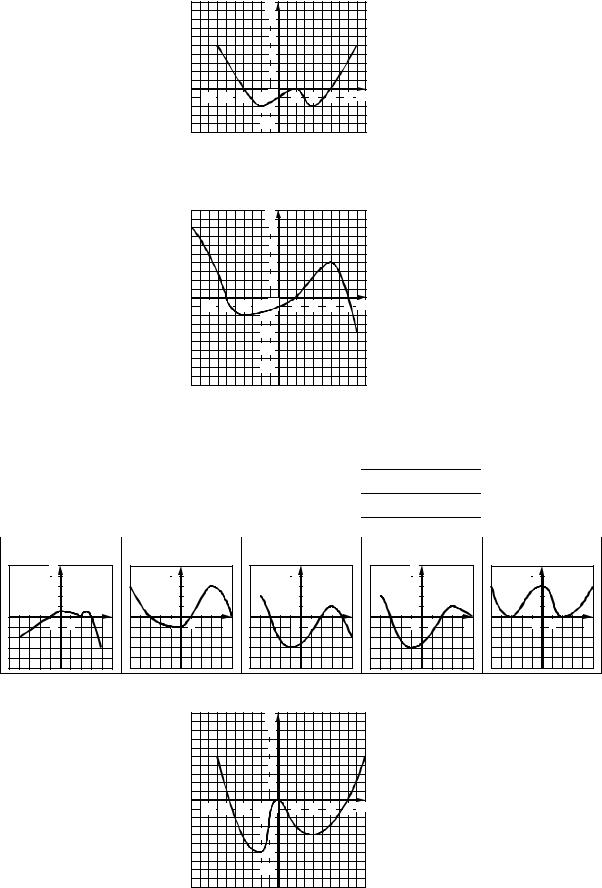
25.17.Вказати усі точки екстремуму функції y = f(x) на відрізку [–3; 4], якщо на рисунку зображено графік функції y = f′(x).

y
4
3
2
1
–4 –3 –2 –1 0	1	2	3	4	x
–1
–2

А	Б	В	Г	Д
–1 і 2	–1; 1 і 2	–2; 1 і 3	–2 і 3	–3 і 4

25.18.Вказати проміжки зростання функції y = ϕ(x) на відрізку [–5; 5], якщо на рисунку зображено графік функції y = ϕ′(x).

y
4
3
2
1
–4 –3 –2 –1 0	1	2	3	4	x
–1
–2
–3
–4

А	Б	В	Г	Д

[–2; 3]	[–1; 2]	[–2; 1] і [4; 5]	[1; 3]	[–5; –3] і [1; 4]

25.19.Функція y = f(x) визначена на множині дійсних чисел; –3 і 2 — нулі функції. Зміну знаків похідної функції подано в таблиці.

(–∞; –1)

–1

(–1; 3)

(3; +∞)

f′(x) < 0

f′(–1) = 0

f′(x) > 0

f′(3) = 0

f′(x) < 0

Який з наведених графіків може бути графіком функції y = f(x)?

0 1

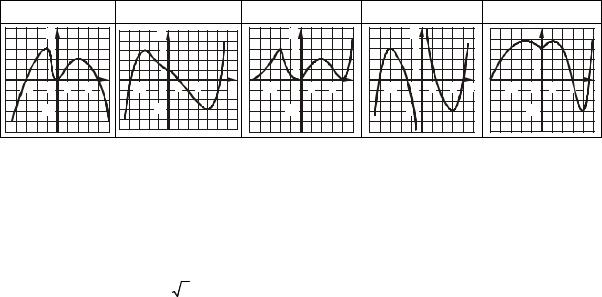
25.20.На рисунку зображено графік функції y = f′(x). Який з наведених графіків може бути графіком функції y = f(x)?

y
4
3
2
1
–4 –3 –2 –1 0	1	2	3	4	x
–1
–2
–3
–4

183

А	Б		В	Г	Д
y	y		y	y	y
3	3		3	3	3
1	1		1	1	1
–3 0 1 3 x	–3 0 1 3	x	–3 0 1 3 x	–3 0 1 3 x	–3 0 1 3 x
–3	–3		–3	–3	–3

25.21. Знайти точку, в якій функція y = xlnx набуває найменшого значення.

25.22. Знайти точку максимуму функції y = ln x .

25.23. За яких значень а функція y =

− x2 + ax має критичні точки, але не має точок екстремумів?

–1

–1 і 1

–4 і 4

25.24. За яких значень а точка 5 є точкою мінімуму функції y = f(x), якщо f′(x) = (x – 5)(x – а)?

а ≥ 5

а = 5

a > 5

a ≤ 5

a < 5

25.25. За яких значень а точка 3 є точкою максимуму функції y =

− a + 3 x2 + 3ax ?

a = 3

a ≥ 3

a ≤ 3

a < 3

a > 3

25.26.

Обчислити найбільше значення функції у = –х3 + 3х2 – 5 на проміжку [–3; 0].

–5

25.27.Рівняння дотичної до кривої у = –х2 + 5х + 4 має вигляд у = 3х + 5. Обчислити абсцису точки дотику.

А	Б	В	Г	Д
1	4	–4	3	–3

25.28.Рівняння дотичної до кривої у = 2х2 – 4х – 1 має вигляд у = 8х – 19. Обчислити ординату точки дотику.

А	Б	В	Г	Д
–1	5	4	3	8

Завдання 25.29–25.42 передбачають установлення відповідності. До кожного рядка, позначеного ЦИФРОЮ, доберіть один відповідник, позначений БУКВОЮ, і поставте позначки на перетині відповідних рядків(цифри) і колонок(букви).

25.29. Установити відповідність між функціями (1–4) та їхніми властивостями (А–Д).

1	y = log1 (x + 2)			А зростаюча на всій області визначення
	2			Б спадна на всій області визначення
2	y = 2	x	+ 2

				В має максимальне значення
3	y = 2x + 2
				Г має найменше значення
4	y = −3x2 + 7x − 14
				Д періодична

184

25.30.Установити відповідність між похідними f′(x) функцій (1–4) та проміжками спадання відповідних їм функцій f(x) (А–Д).

1f′(x) = (x + 1)(x – 5)

2f′(x) = (x + 1)(5 – x)

3f′(x) = (x + 1)2(x – 5)

4f′(x) = (x + 1)(x – 5)2

А (–∞; –1] Б (–∞; 5]

В (–∞; –1] [5; +∞) Г [–5; 1] Д [–1; 5]

25.31.Установити відповідність між похідними f′(x) функцій (1–4) та проміжками зростання відповідних їм функцій f(x) (А–Д).

1f′(x) = (x + 3)(x – 4)

2f′(x) = (x + 3)(4 – x)

3f′(x) = (x + 3)2(x – 4)

4f′(x) = (x + 3)(x – 4)2

А [4; +∞) Б [–3; +∞)

В (–∞; –3] [4; +∞) Г [–3; 4] Д [–4; 3]

25.32. Установити відповідність між функціями (1–4) та проміжками спадання цих функцій (А–Д).

1 у = –3х5 – 4х		А (–∞; 1]
2 у = х4 – 2х2		Б (–∞; 0]
3	у = ex2 − 2x+ 3	В (–∞; –1] [0; 1]
4	у = ех – х	Г [0; +∞)
		Д (–∞; +∞)

25.33. Установити відповідність між функціями (1–4) та проміжками зростання цих функцій (А–Д).

1 у = 3х – х2			А (–∞; +∞)
2	y = 1 − x	2	Б [–1; 0]
			В (–∞; 0] [1; +∞)
3	у = х – lnx
			Г [1; +∞)
4	y = ex + x – 1
			Д (–∞; 1,5]

25.34.Установити відповідність між ескізами графіків функцій (1–4) та кількістю критичних точок цих функцій (А–Д).

1						2						3						4
y						y						y						y
4						4						4						4
3						3						3						3
2						2						2						2
1						1						1						1
–4 –3 –2 –1 0	1	2	3	4	x	–4 –3 –2 –1 0	1	2	3	4	x	–4 –3 –2 –1 0	1	2	3	4	x	–4 –3 –2 –1 0	1	2	3	4	x
–1						–1						–1						–1
–2						–2						–2						–2
–3						–3						–3						–3
–4						–4						–4						–4

	А	Б	В		Г	Д

	Жодної	одна	дві		три	чотири

25.35. Установити відповідність між функціями (1–4) та їх критичними точками (А–Д).
1	у = х5 – 5х		А	1
2	y = x2 + 2		Б	–1
	x		В 0
3	y = ex2 + 2 x		Г 0; 2
4	y = 1− x2		Д –1; 1
4	y = 1− x2

185

25.36.Установити відповідність між похідними f′(x) функцій (1–4) та точками максимуму функцій f(x) (А–Д).

1f′(x) = х(x + 2)(x – 4)

2f′(x) = х2(x + 2)(x – 4)

3f′(x) = х(x + 2)(4 – x)

4f′(x) = х2(x + 2)(4 – x)

А –2

Б 4

В –2; 4 Г –4

Д 0

25.37.Установити відповідність між похідними f′(x) функцій (1–4) та точками мінімуму функцій f(x) (А–Д).

1f′(x) = (х + 3)(x – 1)(x – 5)

2f′(x) = (х + 3)(x – 1)2(x – 5)

3f′(x) = (х + 3)(x – 1)(5 – x)

4f′(x) = (х + 3)(x – 1)2(5 – x)

А 5 Б 1

В –3 Г –1

Д –3; 5

25.38. Установити відповідність між функціями (1–4) та точками максимуму цих функцій (А–Д).

y = −

А 0

Б 1

y =

В –1

Г –1; 0

Д –1; 1

y =

−

y = −

25.39.Установити відповідність між функціями (1–4) та точками мінімуму цих функцій (А–Д).

1	y =		x4			− 2x2		А 0
								Б 2
	4
2	y = −			x		4	+ 2x2	В –2; 2
								Г –2; 0

					4			Д –2
3	y =	x5				− 4x3

	5						3
4	y = −			x5			+ 4x3

25.40.Установити відповідність між параболами (1–4) та ординатами точок (А–Д), у яких кутовий коефіцієнт дотичної до параболи дорівнює 2.

1	у = х2	+ х – 1	А	1,75
2	у = х2 – х + 1		Б –1
3	у = х2 + 2х – 1		В 0
4	у = х2	– 2х + 1	Г –0,25
			Д 1

25.41.Установити відповідність між параболами (1–4) та абсцисами точок (А–Д), у яких кутовий коефіцієнт дотичної до параболи дорівнює 2.

1	у = х2	+ х – 1	А	1,5
2	у = х2 – х + 1		Б 0
3	у = х2 + 2х – 1		В –1
4	у = х2	– 2х + 1	Г	0,5
			Д 2

186

25.42.Установити відповідність між функціями (1–4), заданими на проміжках, та найбільшими значеннями цих функцій на вказаних проміжках.

1у = |x2 – 3x|; x [0; 3]

2у = |–2x2 – 8x|; x [–4; 0]

3у = |9x2 – 18x|; x [0; 2]

4у = |7x2 + 14x|; x [–2; 0]

А 6 Б 8 В 9

Г 2,25

Д 7

Розв’яжіть завдання 25.43–25.57. Відповідь запишіть десятковим дробом.

25.43. Знайти проміжки спадання функції	y = 1 x4 − 1 x2 + 5 . У відповідь записати додатну абсцису
	4	2
середини одного з проміжків спадання.
25.44. Знайти проміжки спадання функції	y = 3x + x2	. У відповідь записати додатну абсцису середи-
	x − 1

ни одного з проміжків спадання.

25.45.Знайти найбільше значення функції y = –2x3 + 6x2 + 9 на відрізку [0; 3].

25.46.Визначити ординату точки перетину осі у з дотичною до графіка функції у = х2 – 3, якщо коефіцієнт дотичної є від’ємним і вона проходить через точку Р(1; –6).

25.47.Визначити ординату точки перетину з віссю ординат дотичної до кривої y = x2 + 2x – 2, яка паралельна до прямої 4х – у – 7 = 0.

25.48.Визначити абсцису точки перетину з віссю абсцис дотичної до кривої у = 3х2 – 3х + 3, яка перпендикулярна до прямої х + 3у – 6 = 0.

25.49.Число 64 подати у вигляді добутку двох додатних множників так, щоб сума їхніх квадратів була найменшою. У відповідь записати найменшу суму квадратів знайдених множників.

25.50.Прямокутну ділянку землі, яка прилягає до стіни будинку, потрібно обгородити парканом завдовжки 160 метрів. Знайти довжину прямокутника в метрах, за якої площа ділянки буде найбільшою.

25.51.Визначити висоту в метрах відкритого басейну із квадратним дном, об’єм якого дорівнює 32 м3, такого, щоб на облицювання його стін і дна витрати на матеріал, були найменшими.

25.52.За якого найменшого цілого значення а функція y = x3 + 3x2 + ax – 1 не має критичних точок?

25.53.За якого від’ємного значення b один із екстремумів функції y = 2x3 – 3x2 + b дорівнює –1?

25.54.За якого найбільшого значення а функція y = xex є спадною на проміжку [a – 5; a + 3]?

25.55.Обчислити найбільше ціле значення параметра а, за якого функція у = 5х + (–а + 7,(6))х зростає на всій числовій прямій.

25.56.Обчислити найменше ціле значення параметра а, за якого функція у = х3 + ах2 + х + 1 зростає на всій числовій прямій.

25.57.Знайти, за яких значень параметра а сума кубів коренів рівняння 6x2 + 6(a – 1)x – 5a + 2a2 = 0 буде найбільшою.

187

ТЕМА 26. ПЕРВІСНА. ІНТЕГРАЛ

Завдання 26.1–26.32 мають по п’ять варіантів відповідей, з яких тільки ОДНА ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь.

26.1.Знайти загальний вигляд первісних для функції f(x) = x10 – x8 + x + 13.

F(x) =

x11

−

F(x) =

x11

−

F(x) = −

x11

−

F(x) = 10x9 –

F(x) = 11x11 – 9x9 +

11 9

– 8x + 1 + C

+ 13x + C

+ 13 + C

+ 2x + 13x + C

−

− 13x + C

26.2. Знайти загальний вигляд первісних для функції f(x) = –4cosx.

F(x) = –4sinx + C

F(x) = 4sinx + C

F(x) = –4cosx + C

F(x) = 4cosx + C

F(x) = –16cosx + C

26.3.

Вказати загальний вигляд первісної для функції

f (x) = cos2

F(x) = 1 x + sin x + C

F(x) = 1 x + sin

+ C

F(x) = x + sin

+ C

F(x) = 1 x + sin

+ C

F(x) = 1 x + 1 sin

+ C

26.4.

Вказати загальний вигляд первісної для функції

f (x) = sin2 x − 4cos2 x .

sin x − 2cos x

F(x) = cos x + 2sin x + C

F(x) = cos x − 2sin x + C

F(x) = − cos x + 2sin x + C

F(x) = − cos x + 1 sin x + C

F(x) = − 1 cos x + 1 sin x + C

26.5.

Яка з функцій задовольняє рівняння f ′ (x) =

sin2

f(x) = 10tgx

f(x) = –10ctgx

f(x) = –10tgx

f (x) = −

ctg x

f(x) = 10ctgx

26.6.

Для функції f(x) = sinx знайти первісну F(x), графік якої проходить через точку О(0; 0).

F(x) = sinx

F(x) = cosx

F(x) = cosx + 1

F(x) = 1 – cosx

F(x) = cosx – 1

26.7.Обчислити інтеграл 1 x20dx .

А	Б	В		Г		Д
19	21	20		1		1
19	21	20	20		21
			20		21

188

26.8.Обчислити 1 (x2 − 4x)dx .

А	Б	В	Г	Д
5	1	2	− 5	7
3	3		3	3

26.9.Обчислити 1 2x5dx .

					1							1						− 1					1						1
					2							3						3											4
26.10. π sin			x	dx = ...
26.10. π sin				dx = ...
0		2
0

					А							Б						В					Г						Д
			2cos x			π				−	1	cos	x	π		1	cos		x	π		−2cos				x	π	2cos		x		π
						π					1		x	π		1			x	π						x	π			x		π
						0								0							0						0					0
						0					2		2			2		2			0				2		0			2		0
											2		2			2		2							2					2
							(		)	π					dx .
							(		)
								10
26.11. Обчислити: 80								3 + 1 sin 10x + π
										π				3
								20

					А							Б						В					Г						Д
					0,8						1 −		3					–0,8					8						–8
					0,8							20						–0,8					8						–8
												20

26.12. Тіло рухається прямолінійно зі швидкістю v(t) = 2t + 1.																						Знайти закон руху тіла S(t), якщо
	S(1) = 3.

					А							Б						В					Г						Д
		S(t) = t2 + t + 3								S(t) = t2 + t						S(t) = t2 + t + 1						S(t) = t2 + t + 2						S(t) = t2 + t – 1
26.13.	Вказати інтеграл для обчислення площі фігури, обмеженої лініями y = x2, y = 0 і x = 2.
					А							Б						В					Г						Д
				4	x2dx					2 (x2 − x)dx							2	2xdx				2	x3		dx			2	x2dx
				4	x2dx					2 (x2 − x)dx							2	2xdx				2	3		dx			2	x2dx
		0							0								0					0	3					0
		0							0								0					0						0
26.14.
26.14.	Вказати формулу для обчислення площі S фігури, обмеженої лініями y = x2 і y = x.
					А							Б						В					Г						Д

		S = 1 (x2 − x)dx							S = 1 (x2 + x)dx							S = 1 (x − x2 )dx						S = 1		x2dx				S = 1			xdx
		0									0					0							0						0

26.15. Вказати формулу для обчислення площі фігури, зображеної на рисунку.

y
2		y=f(x)
1		y=f(x)
1
–1 0	1	2	3	4	x
–1
–2

189

S = 2

f (x)dx −

S = 2

f (x)dx +

S = 2

f (x)dx −

S = f (x)dx

S = 2 f (x)dx

(x)dx

− f (x) dx

+ f

− f (x)dx

26.16. Обчислити площу фігури, обмеженої графіками функцій у = cosx,

x = − 5π , x = π та віссю х.

3,5 кв. од.

3 кв. од.

5 кв. од.

2,5 кв. од.

4,5 кв. од.

26.17.

Обчислити площу

фігури, обмеженої

графіками функцій

у = х + 3 та у = х2 +

3,5 кв. од.

3 кв. од.

5 кв. од.

2,5 кв. од.

4,5 кв. од.

26.18.

Обчислити площу

фігури, обмеженої

графіками функцій

у = x, у = 7 – x, х =

1 та х = 3.

3,5 кв. од.

6 кв. од.

4,5 кв. од.

4 кв. од.

5,5 кв. од.

26.19.

Знайти загальний

вигляд первісних для функції f(x) = cos2x.

F(x) =

−

F(x) =

F(x) = 1 +

F(x) = –sin2x + C

+ 1 sin 2x + C

− 1 sin 2x + C

+ sin 2x + C

+ 1 cos 2x + C

26.20. Вказати загальний вигляд первісної для функції f (x) = xe− x2 .

F(x) = 1 e− x2 + C

F(x) = e− x2 + C

F(x) = 2e− x2 + C

F(x) = − 1 e− x2 + C

F(x) = − 1 ex2 + C

26.21. Вказати загальний вигляд первісної для функції f (x) =

x ln x

F(x) = ln x + C

F(x) = 2ln x + C

F(x) =

ln x

+ C

F(x) = 2 ln x + C

F(x) =

ln x

+ C

26.22.

Вказати загальний вигляд первісної для функції

f(x) = sin–2x + cos–2x.

F(x) = –tgx + ctgx + C

F(x) = − 1 sin−3 xcos−3 x

F(x) = tgx – ctgx + C

190

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 1819 / 3419 20 21 22 23 24 25 26 27 28 29 30 31 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.08.2019152.06 Кб34тести до всіх решти тем з економіки.doc
#
08.01.2020955.39 Кб0Тести друк.doc
#
08.01.2020938.5 Кб0Тести з педагогіки І і ІІ рівні (з відповідями)...doc
#
08.01.2020904.19 Кб0Тести з педагогіки І і ІІ рівні.doc
#
14.02.201675.2 Кб42тести на соціологію (модуль1).docx
#
14.02.20162.86 Mб4520ТЕСТИ_ЗНО_МАТЕМ.pdf
#
02.01.2020121.86 Кб0Техніка безпеки змагань зі спортивного туризму.doc
#
14.02.2016126.98 Кб9Техніка мовлення.doc
#
05.09.201934.58 Кб17ТЕХНІКА ПЛАВАННЯ СПОСОБОМ КРОЛЬ.docx
#
11.11.201933.2 Кб4технічні засоби виробн..docx
#
14.02.20162.07 Mб80Техническая подготовка боксера.docx