
- •Міністерство освіти і науки україни
- •Розділ і електронні підручники як засіб підтримки учбового процесу
- •Розділ іі технологія створення електронного підручника
- •1. Інструментальне забезпечення. Редактор FrontPage
- •1.1 Вставка тексту
- •1.2 Використання спеціальної вставки
- •1.3 Виділення тексту
- •1.4 Копіювання
- •1.5 Видалення тексту
- •1.6 Розриви тексту
- •1.7 Шаблони
- •1.8 Шаблони сайтів
- •1.9 Шаблони сторінок
- •1.10 Створення фреймів
- •1.11 Шрифти
- •1.12 Символи
- •1.13 Форматування абзаців
- •1.14 Списки
- •1.15 Створення гіперпосилань
- •1.16 Графічні формати
- •1.17 Збереження зображень
- •1.18 Колекція ілюстрацій
- •2 Характеристика та етапи створення електронного підручника
- •Розділ ііі ряди Числові ряди.
- •1.2 Знакододатні ряди. Умови збіжності таких рядів.
- •1.3 Абсолютно та умовно збіжні ряди
- •1.4 Ознаки збіжності знакозмінних рядів.
- •1.5 Множення рядів
- •Функціональні послідовності та ряди
- •2.1 Збіжність, рівномірна збіжність функціональних рядів і послідовностей
- •2.2 Властивості рівномірно збіжних послідовностей і рядів
- •Степеневі ряди
- •3.1 Область збіжності степеневого ряду. Властивості сум степеневих рядів
- •3.2 Розклад функції у степеневий ряд. Біноміальний ряд
- •Висновок
- •Список використаної літератури
1.5 Множення рядів
Вище ми згадували про додавання та множення на константу рядів, а як же перемножити між собою два ряди? Чи завжди добуток двох збіжних рядів буде збіжним рядом? В цьому розділі ми дамо відповіді на ці запитання.
Розглянемо поняття добутку двох рядів за Коші.
Означення (Коші). Під добутком рядів
![]() ,
(1)
,
(1)
![]() (2)
(2)
за Коші, розуміють такий ряд
![]() ,
де
,
де
![]() .(3)
.(3)
Виявляється, що якщо ряди (1) і (2) – збіжні, то цього мало для збіжності ряду (3) (добутку їх за Коші).
Приклад.
Нехай ми маємо два ряди
![]() і
і![]() ,
утворимо добуток цих рядів
,
утворимо добуток цих рядів
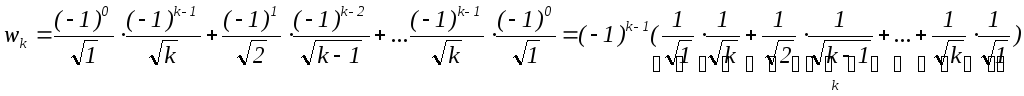
В![]() зявши
зявши![]() по модулю ми побачимо, що кожен доданок
в дужках більший або рівний за
по модулю ми побачимо, що кожен доданок
в дужках більший або рівний за![]() ,
то врахувавши, що кількість доданків
,
то врахувавши, що кількість доданків![]() ,
матимемо, що
,
матимемо, що![]() і не прямує до нуля, а отже, ряд –
розбіжний. Таким чином, ми встановили,
що добуток двох збіжних рядів не
зобов’язаний бути збіжним рядом.
і не прямує до нуля, а отже, ряд –
розбіжний. Таким чином, ми встановили,
що добуток двох збіжних рядів не
зобов’язаний бути збіжним рядом.
Зауважимо, що обидва співмножники є умовно збіжними рядами. Можливо, негативний результат одержався саме з цієї причини? Відповідь на цю проблему дає наступне твердження.
Теорема.
(Мертенс). Нехай ряд (1) абсолютно збіжний,
а ряд (2) – збіжний. Тоді ряд (3) – збіжний
до числа
![]() ,
де
,
де![]() і
і![]() – суми
рядів відповідно (1) і (2).
– суми
рядів відповідно (1) і (2).
▲
Нехай
![]() ,
,![]() ,
,![]() – часткові суми відповідно рядів (1),
(2), (3). Розглянемо
– часткові суми відповідно рядів (1),
(2), (3). Розглянемо![]()
![]()
![]() (4)
(4)
Оскільки
ряд (2) – збіжний до суми
![]() ,
то
,
то![]() ,
а отже,
,
а отже,![]() ,
де
,
де![]() при
при![]() .
Звідси і з (4) маємо, що
.
Звідси і з (4) маємо, що![]() .
Для доведення цієї теореми достатньо
показати, що
.
Для доведення цієї теореми достатньо
показати, що
![]() .
(5)
.
(5)
З абсолютної збіжності ряду (1) маємо, що
![]()
![]() ,
(6)
,
(6)
де
![]() – це число, що визначається з того, що
нескінченно мала послідовність
– це число, що визначається з того, що
нескінченно мала послідовність![]() .
– обмежена, і
.
– обмежена, і
![]() .
(7)
.
(7)
Оцінимо
тепер
![]() ,
,
![]()
![]() .
Із збіжності ряду
.
Із збіжності ряду
![]() ,
випливає, що його сума дорівнює деякому
числу
,
випливає, що його сума дорівнює деякому
числу![]() ,
тоді
,
тоді
![]() ,
,
![]() .(8)
.(8)
Оскільки
![]() ,
то для вказаного в (6)
,
то для вказаного в (6)![]() знайдеться
знайдеться![]()
![]() .
(9)
.
(9)
Повертаючись
до оцінки
![]() візьмемо
візьмемо![]() ,
тоді на основі (9) та (8) матимемо, що
,
тоді на основі (9) та (8) матимемо, що![]() ,
а це і означає, що ряд (3) – збіжний.
,
а це і означає, що ряд (3) – збіжний.
▼
Зауважимо, що в теремі Мертенса умова абсолютної збіжності одного з рядів не може бути знятою.
Функціональні послідовності та ряди
2.1 Збіжність, рівномірна збіжність функціональних рядів і послідовностей
Послідовність
![]() членами якої є функції
членами якої є функції![]() ,
кожна з яких визначена на множині
,
кожна з яких визначена на множині![]() ,
називається функціональною послідовністю
визначеною на
,
називається функціональною послідовністю
визначеною на![]() .Аналогічно,
.Аналогічно,![]() ,
де
,
де![]() функції, кожна з яких визначена на
функції, кожна з яких визначена на![]() ,
називається функціональним рядом
визначеним на
,
називається функціональним рядом
визначеним на![]() .
Як і для числових рядів і послідовностей,
так і для функціональних, між ними існує
зв'язок, який дозволяє отримані результати
для одного з об’єктів перекидати на
інший.
.
Як і для числових рядів і послідовностей,
так і для функціональних, між ними існує
зв'язок, який дозволяє отримані результати
для одного з об’єктів перекидати на
інший.
Візьмемо
точку
![]() з множини
з множини![]() .
Підставимо цю точку
.
Підставимо цю точку![]() в ряд
в ряд![]() ,
одержимо числовий ряд
,
одержимо числовий ряд![]() ,
який може бути або збіжним, або розбіжним.
Якщо цей числовий ряд буде збіжним, то
точку
,
який може бути або збіжним, або розбіжним.
Якщо цей числовий ряд буде збіжним, то
точку![]() називають точкою збіжності цього ряду.
Множина всіх таких точок множини
називають точкою збіжності цього ряду.
Множина всіх таких точок множини![]() називається областю збіжності
функціонального ряду. Якщо її позначимо
через
називається областю збіжності
функціонального ряду. Якщо її позначимо
через![]() ,
то зрозуміло, що
,
то зрозуміло, що![]() .
Сумою функціонального ряду на області
збіжності
.
Сумою функціонального ряду на області
збіжності![]() буде деяка функція
буде деяка функція![]() задана на цій множині. Очевидно, що
область збіжності функціонального
ряду можна шукати використовуючи ознаки
збіжності числових рядів.
задана на цій множині. Очевидно, що
область збіжності функціонального
ряду можна шукати використовуючи ознаки
збіжності числових рядів.
Приклад.
Розглянемо послідовність
![]() ,
де
,
де![]() на
на![]() задається так,
задається так,
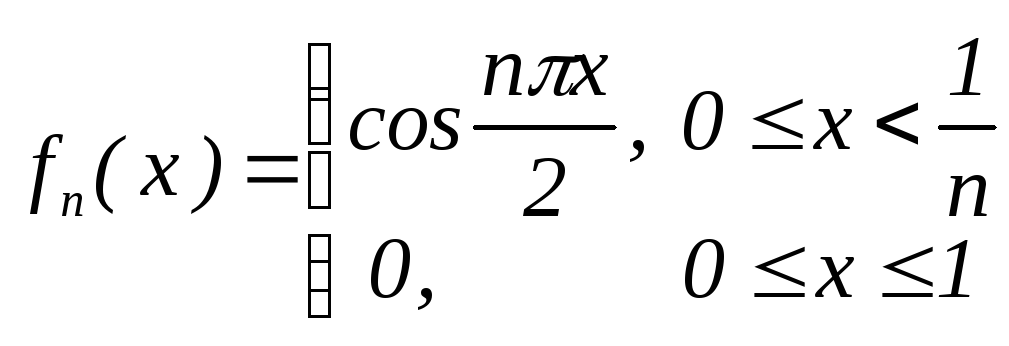
Зрозуміло,
що послідовність
![]() збіжна при
збіжна при![]() до функції
до функції
![]()
Цей
приклад показує, що границя послідовності
неперервних функцій не зобов’язана
бути неперервною функцією. Далі ми ще
повернемось до цієї проблеми, але спершу
напишемо, що означає, що
![]() :
:
![]() (1)
(1)
Умова
(1) виражає собою, так звану, поточкову
збіжність послідовності на множині
![]() .
.
Оскільки
поточкова збіжність приводить до не
зовсім бажаних результатів (границя
послідовності неперервних функцій не
зобов’язана бути неперервною функцією),
то спробуємо дещо підсилити означення
збіжності (1).В поточковій збіжності
номер
![]() залежить і від
залежить і від![]() ,
і від вибору точки
,
і від вибору точки![]() з множини
з множини![]() .
Спробуємо одержати таку збіжність, щоб
.
Спробуємо одержати таку збіжність, щоб![]() залежало лише від
залежало лише від![]() і підходило одразу до всіх
і підходило одразу до всіх![]() з
з![]() (
тобто, щоб воно від
(
тобто, щоб воно від![]() не залежало). Це вже буде не поточкова
збіжність. Її ми назвемо рівномірною
збіжністю на множині
не залежало). Це вже буде не поточкова
збіжність. Її ми назвемо рівномірною
збіжністю на множині![]() .
.
Дамо тепер точне означення цьому поняттю.
Означення.
Послідовність
![]() називається рівномірно збіжною на
множині
називається рівномірно збіжною на
множині![]() до функції
до функції![]() ,
якщо
,
якщо
![]() .
(2)
.
(2)
Зрозуміло, що означення рівномірної збіжності легко переноситься і на ряди.
Означення.
Ряд
![]() називається рівномірно збіжним на
множині
називається рівномірно збіжним на
множині![]() до функції
до функції![]() ,
якщо рівномірно збіжною на
,
якщо рівномірно збіжною на![]() є послідовність його часткових сум, або
що те саме,
є послідовність його часткових сум, або
що те саме,
![]() .
(3)
.
(3)
Зрозуміло, що із рівномірної збіжності на множині, випливає поточкова збіжність, а навпаки? Наступна теорема в якісь мірі відповідає на питання , що дає рівномірна збіжність послідовності.
Теорема1.
Нехай
![]() – послідовність функцій, неперервних
в точці
– послідовність функцій, неперервних
в точці![]() ,
яка рівномірно збіжна до функції
,
яка рівномірно збіжна до функції![]() в деякому
в деякому![]() -
та околі точки
-
та околі точки![]() .
Тоді
.
Тоді![]() – неперервна в цій точці.
– неперервна в цій точці.
▲
З умови теореми випливає, що
![]() .
(4)
.
(4)
Розглянемо
різницю поки що для
![]() ,
(далі
,
(далі![]() – якесь натуральне число більше за
– якесь натуральне число більше за![]() )
)
![]()
![]() (5)
(5)
Оскільки
функція
![]() – неперервна в точці
– неперервна в точці![]() ,
то для вказаного вище
,
то для вказаного вище![]()
![]()
![]() .
Взявши в (5)
.
Взявши в (5)![]() ,
матимемо, що
,
матимемо, що![]() ,
а це і означає, що
,
а це і означає, що![]() неперервна в точці
неперервна в точці![]() .
.
▼
Очевидно, з цієї теореми, в якості простого наслідку випливає наступна
Теорема2.
Якщо послідовність
![]() – рівномірно збіжна до
– рівномірно збіжна до![]() на відрізку
на відрізку![]() і
і![]()
![]() – неперервні на
– неперервні на![]() функції, то
функції, то![]() теж неперервна на цьому відрізку.
теж неперервна на цьому відрізку.
Цими теоремами ми не лише показали важливість рівномірної збіжності, а і з врахуванням приведеного вище прикладу встановили, що із поточкової збіжності, рівномірна збіжність не випливає. Тобто поняття цих двох збіжностей не є еквівалентними (друге є більш „жорстким”).
Теорема3.
(Критерій Коші рівномірної збіжності
послідовності). Для того щоб послідовність
![]() рівномірно збігалася на множині
рівномірно збігалася на множині![]() ,
необхідно і достатньо, щоб
,
необхідно і достатньо, щоб
![]() .
(6)
.
(6)
▲
Необхідність. Доведення необхідності в цьому випадку аналогічне до доведення необхідності в критерії Коші для числових послідовностей.
Достатність. Нехай
![]() .
(7)
.
(7)
Підставимо
в (7) замість
![]() будь-яку фіксовану точку з множини
будь-яку фіксовану точку з множини![]() .
Ми отримаємо числову послідовність
.
Ми отримаємо числову послідовність![]() ,
яка за (7) на основі критерію Коші для
числової послідовності є збіжною. Отже,
ми одержали, що послідовність
,
яка за (7) на основі критерію Коші для
числової послідовності є збіжною. Отже,
ми одержали, що послідовність![]() збіжна на
збіжна на![]() до деякої функції
до деякої функції![]() .
Доведемо, що ця збіжність – рівномірна.
Для цього звернемося до останньої
нерівності з (7). Перейшовши в ній до
границі, коли
.
Доведемо, що ця збіжність – рівномірна.
Для цього звернемося до останньої
нерівності з (7). Перейшовши в ній до
границі, коли![]() ,
і врахувавши, що
,
і врахувавши, що![]() ,
ми отримаємо, що послідовність
,
ми отримаємо, що послідовність![]() збігається рівномірно на множині
збігається рівномірно на множині![]() .
.
▼
Теорема4.
Для того, щоб ряд був рівномірно збіжним
на множині
![]() ,
необхідно і достатньо, щоб
,
необхідно і достатньо, щоб![]() .
.
Хоча теореми 3 і 4 – це критерії рівномірної збіжності, проте, на практиці застосовувати їх важко. Тому є потреба одержати більш конструктивні, хоча б достатні умови рівномірної збіжності. Виявляється, що для послідовностей часто ефективним є наступний критерій.
Теорема5.
(Критерій рівномірної збіжності
послідовності). Для того, щоб послідовність
![]() рівномірно збігалась до
рівномірно збігалась до![]() на множині
на множині![]() ,
необхідно і достатньо, щоб
,
необхідно і достатньо, щоб![]() ,
де
,
де![]() .
.
▲
Необхідність.
Нехай
![]() рівномірно збігається до
рівномірно збігається до![]() .
Тоді,
.
Тоді,
![]() .
Звідси випливає, що
.
Звідси випливає, що
![]() .
А це і означає, що
.
А це і означає, що![]() .
.
Доведення достатності є очевидним.
▼
Для рядів корисною є наступна
Теорема6.
(Ознака Вейерштрасса). Нехай
![]() – деякий ряд і
– деякий ряд і![]() – збіжний знакододатній ряд. Якщо для
– збіжний знакододатній ряд. Якщо для![]() і для всіх
і для всіх![]() справедлива нерівність
справедлива нерівність
![]() ,
(8)
,
(8)
то ряд
![]() рівномірно і абсолютно збіжний на
множині
рівномірно і абсолютно збіжний на
множині![]() .
.
▲
Для
доведення теореми достатньо розглянути
нерівність
![]() ,
,![]() і використати критерій Коші для числових
рядів і теорему4.
і використати критерій Коші для числових
рядів і теорему4.
▼
Зауважимо,
що в цій теоремі, ряд
![]() називається мажорант ним рядом для
нашого функціонального ряду. Отже, щоб
застосувати теорему Вейерштрасса,
потрібно для досліджуваного на рівномірну
збіжність функціонального ряду, на
множині
називається мажорант ним рядом для
нашого функціонального ряду. Отже, щоб
застосувати теорему Вейерштрасса,
потрібно для досліджуваного на рівномірну
збіжність функціонального ряду, на
множині![]() підібрати збіжний мажорант ний ряд.
Інколи такого ряду може і не існувати,
але це не означає що ряд не буде рівномірно
збіжним на
підібрати збіжний мажорант ний ряд.
Інколи такого ряду може і не існувати,
але це не означає що ряд не буде рівномірно
збіжним на![]() .
А що ж робити у такому випадку? Виявляється,
як і для числових рядів були ефективні
ознаки Абеля-Діріхле, так і тут, на їх
базі утворюють відповідні ознаки
рівномірної збіжності функціональних
рядів.
.
А що ж робити у такому випадку? Виявляється,
як і для числових рядів були ефективні
ознаки Абеля-Діріхле, так і тут, на їх
базі утворюють відповідні ознаки
рівномірної збіжності функціональних
рядів.
Перед формулюванням цих ознак введемо таке поняття.
Означення.
Послідовність
![]() називається рівномірно обмеженою на
множині
називається рівномірно обмеженою на
множині![]() ,
якщо
,
якщо![]() і
і![]() .
.
Теорема7.
(Перша ознака Абеля-Діріхле рівномірної
збіжності ряду). Нехай маємо ряд
![]() і
і![]() .
Якщо:
.
Якщо:
послідовність
 – рівномірно обмежена на
– рівномірно обмежена на ;
;послідовність
 – монотонна для
– монотонна для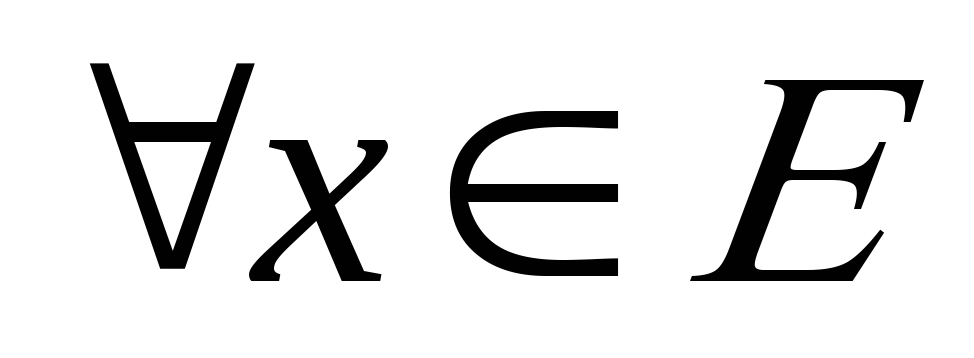 ;
;послідовність
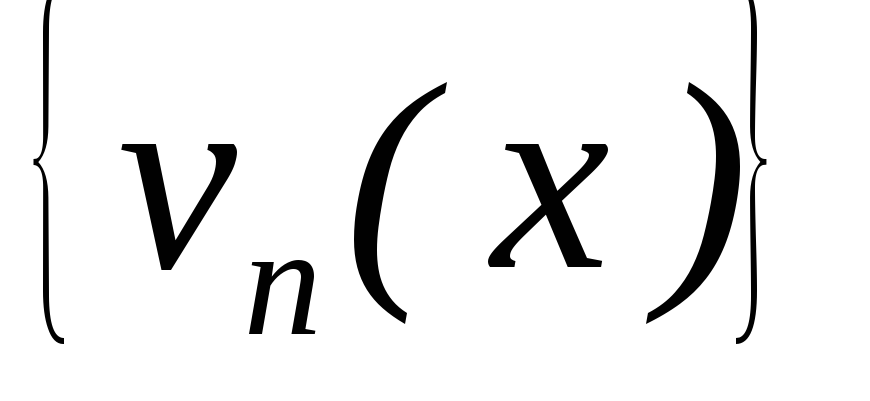 – рівномірно збіжна на
– рівномірно збіжна на до нуля,
до нуля,
тоді
ряд
![]() рівномірно збіжний на множині
рівномірно збіжний на множині![]() .
.
Теорема
8.
(Друга ознака Абеля-Діріхле рівномірної
збіжності ряду). Нехай маємо ряд
![]() і
і![]() .
Якщо:
.
Якщо:
послідовність
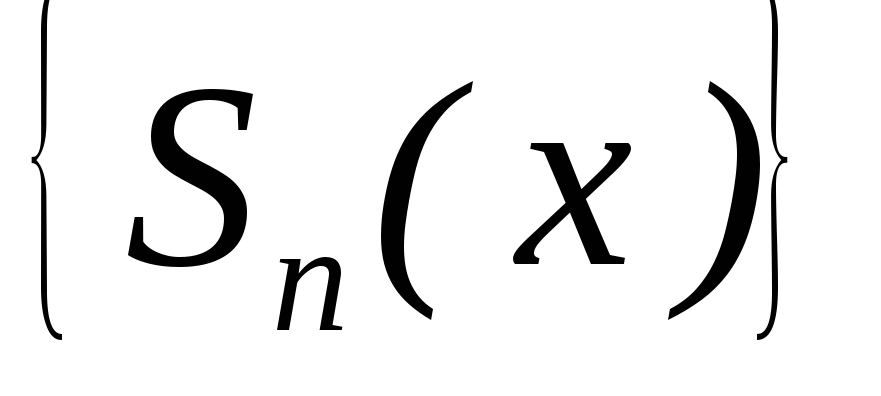 – рівномірно збіжна на
– рівномірно збіжна на ;
;послідовність
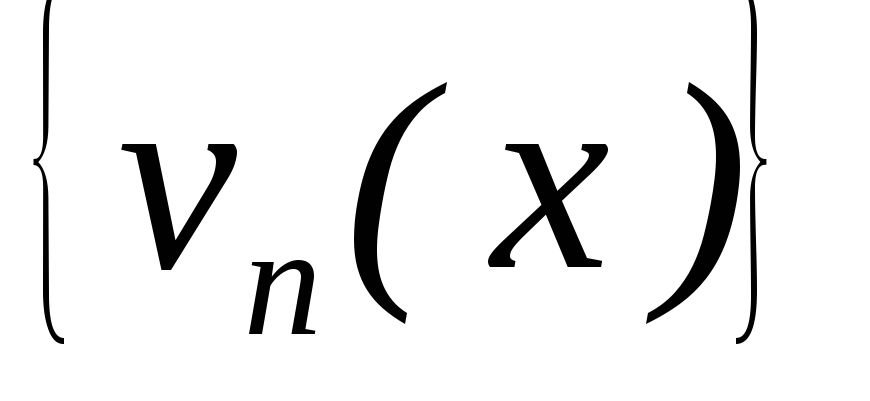 – монотонна для
– монотонна для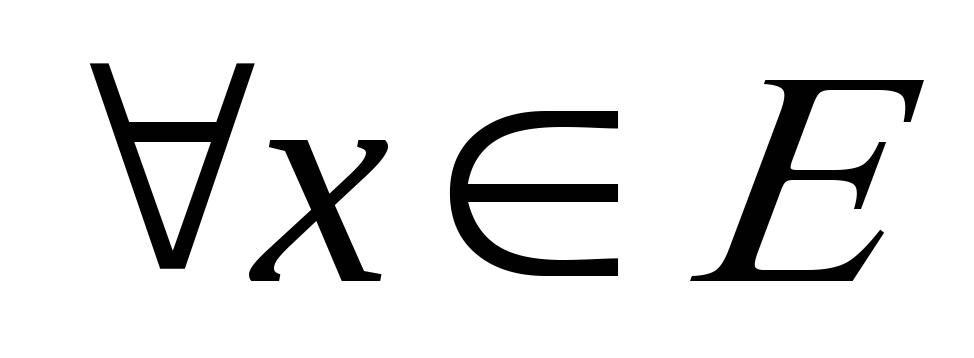 ;
;послідовність
 – рівномірно обмежена на
– рівномірно обмежена на ,
,
тоді
ряд
![]() рівномірно збіжний на множині
рівномірно збіжний на множині![]() .
.
Доведення цих ознак одержується перенесенням аналогічних ознак, для числових рядів лише з певними змінами. Правда, для доведення теореми 8 потрібне перетворення Абеля в дещо іншій формі. Напишемо цю іншу форму з якої і одержиться дана теорема.
Нехай
маємо ряд
![]() ,
,![]()
![]() ,
(при цьому вважатимемо, що
,
(при цьому вважатимемо, що![]() ).
Тоді матимемо
).
Тоді матимемо
![]() .
(9)
.
(9)
Доведення теореми 7.
▲
Позначимо
для
![]() ,
,![]() .
Будемо вважати, що
.
Будемо вважати, що![]() .
.
З умови
1) цієї теореми
![]()
![]() ,
а отже, для
,
а отже, для![]()
![]() .
(10)
.
(10)
З умови
3) теореми 7 маємо,
![]() ,
,
![]() .
(11)
.
(11)
Візьмемо
для конкретності
![]() – монотонно зростаюча. Тоді, скориставшись
рівністю (9) і монотонністю
– монотонно зростаюча. Тоді, скориставшись
рівністю (9) і монотонністю![]() ,
,![]() ,
будемо мати
,
будемо мати
![]()
![]()
![]() ,
а це за критерієм Коші означає рівномірну
збіжність ряду
,
а це за критерієм Коші означає рівномірну
збіжність ряду
![]() на множині
на множині![]() .
.
Зауважимо,
що ми в наших випадках в доведенні
використовували те, що
![]() (бо
(бо![]() монотонно зростає до нуля!).
монотонно зростає до нуля!).
▼
Доведення теореми 8.
▲
З умови
3) цієї теореми маємо, що
![]()
![]() .
(12)
.
(12)
З умови
1) за критерієм Коші рівномірної збіжності
отримаємо,
![]() ,
,
![]() .
(13)
.
(13)
Візьмемо
для конкретності, що послідовність
![]() монотонно спадна. Тоді з (9),
монотонно спадна. Тоді з (9),![]() ,
,![]() ,
будемо мати,
,
будемо мати,![]()
![]()
![]() ,
а це знову за критерієм Коші рівномірної
збіжності ряду означає, що ряд
,
а це знову за критерієм Коші рівномірної
збіжності ряду означає, що ряд
![]() – рівномірно збіжний на множині
– рівномірно збіжний на множині![]() .
.
▼
Отже, ми привели декілька теорем які є або критеріями, або ознаками рівномірної збіжності рядів і послідовностей. Вище ми довели теорему, яка показує, що рівномірно збіжні послідовності (а отже і ряди) можуть мати властивості, яких не мають поточково збіжні ряди і послідовності. В наступному параграфі ми розширимо перелік таких властивостей.
