
- •19 Экстремум функции. Необходимое усл.
- •20. Исследование функции.
- •21. Первообр. Функции и неопр. Интеграл. Св-ва неопр. Инт. Таблица неопр. Интегр.
- •31. Линии уровня. Градиент.
- •22. Интегрирование по частям и замена переменных в неопределённом интеграле.
- •23. Опред. Интеграл. Осн. Свойства опред. Интеграла.
- •24 Теорема Ньютона-Лейбница.
- •25.Замена переменной и интегрирование по частям в определенном интеграле. Метод замены переменной
- •26.Площадь плоской фигуры. Объем тела вращения.
- •27. Несобственныеинт. 1го и 2го порядка.
- •28. Среднее значение ф-и на отрезке. Теорема о среднем значении ф-и.
- •30. Экстремум ф-и нескольких переменных. Необходимое усл-е эктремума.
- •29. Ф-и нескольких переменных.
- •32. Частные производные ф-й 2-х переменных.
- •33. Полный дифференциал ф-й 2-х переменных.
- •34. Частные производные высших порядков.
- •35. Независимость частных производных от порядка дифференцирования.
- •36. Метод наименьших квадратов.
- •37. Числовые ряды, частные суммы числовых рядов.
- •38. Признаки сходимости ряда
- •39. Теоремы о сходимости числовых рядов.
- •40. Эталонные ряды для установления сходимости
- •41. Функциональные ряды, степенные ряды, ряды Тейлора и Маклорена
- •42.Теорема Абеля о сходимости степенного ряда:
- •43.Разложение основных элементарных функций.
- •44. Показательная и тригонометрическая функция комплексной переменной, их связь
- •45. Ряд Фурье. Коэффициенты ряда Фурье. Сходимость рядов Фурье.
- •46. Дифференциальные уравнения (основные понятия)
- •47. Дифференциальныеур-я 1-го порядка с разделяющимися переменными:
- •48. Однородные дифференциальные уравнения
- •49. Линейные дифференциальные уравнения с постоянными коэффициентами
37. Числовые ряды, частные суммы числовых рядов.
 -числовой
ряд.
-числовой
ряд.
Среди числ. рядов выделяют знакопостоянные, знакочередующиеся, знакопеременные.
Частичной суммой рядасоответсв. номеруnназ. суммаnпервых его слагаемых.
 -
частичная сумма.
-
частичная сумма.
Ряд anназ. сходящимся, если последовательность
частичных сумм для этого ряда имеет
предел, т.е. если сущ-т число .
Это число наз.суммой ряда.
.
Это число наз.суммой ряда.
38. Признаки сходимости ряда
Пусть задана бесконечная
последовательность чисел
 .
Выражение
.
Выражение . наз-ют
числовым рядом. При этом числа
. наз-ют
числовым рядом. При этом числа
 наз. членами ряда.
наз. членами ряда.
Числовой ряд часто записывают
в виде .Теорема (необходимый
признак сходимости ряда):если ряд
сходится, то его n-й
член стремится к нулю при неограниченном
возрастании n.
.Теорема (необходимый
признак сходимости ряда):если ряд
сходится, то его n-й
член стремится к нулю при неограниченном
возрастании n.
Следствие. Если n-й
член ряда не стремится к нулю при  ,
то ряд расходится.
,
то ряд расходится.
Признак Даламбера— признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г.
Если для числового ряда существует
такое числоq, что 0<q<1,
ичто, начиная с некоторого номера,
выполняется неравенство
существует
такое числоq, что 0<q<1,
ичто, начиная с некоторого номера,
выполняется неравенство ,
то данный ряд абсолютно сходится;
если же, начиная с некоторого номера
,
то данный ряд абсолютно сходится;
если же, начиная с некоторого номера – абсолютно расходится.
– абсолютно расходится.
39. Теоремы о сходимости числовых рядов.
Определение.Частной суммой
числового ряда называетсясумма
называетсясумма .
Числовой ряд называетсясходящимся,
если существует предел
.
Числовой ряд называетсясходящимся,
если существует предел ,
при этомS называется
суммой ряда.
,
при этомS называется
суммой ряда.
Теорема.Числовой ряд сходится
тогда и только тогда, когда для
любого существует
такое
существует
такое ,
что для всехm,n>
,
что для всехm,n> <
< .
.
Доказательство.
Заметим, что
 .
После этого утверждение превращается
в критерий Коши сходимости
последовательности
.
После этого утверждение превращается
в критерий Коши сходимости
последовательности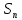 .
.
Теорема.
Если ряд  сходится,
то
сходится,
то .
.
Доказательство.
Из свойств пределов следует, что  .
Отсюда следует, что
.
Отсюда следует, что .
.
40. Эталонные ряды для установления сходимости
Геометрический ряд
![]() Обобщеный
гармонический ряд
Обобщеный
гармонический ряд
![]()
В частности, при к=1 получаем гармонический ряд
![]() Эталонные
ряды, т.е. разложения элементарных
функций, можно использовать для получения
рядов тех же функций, но сложного
аргумента.
Эталонные
ряды, т.е. разложения элементарных
функций, можно использовать для получения
рядов тех же функций, но сложного
аргумента.
41. Функциональные ряды, степенные ряды, ряды Тейлора и Маклорена
Пусть функции Un(x),n∈N,
определены в области D. Выражение U1(x)
+ U2(x)
+… + Un(x)+…=
 Un(x),
где х∈D,
наз. функциональным
рядом. Каждому
значению x0∈D
соответствует числовой ряд
Un(x),
где х∈D,
наз. функциональным
рядом. Каждому
значению x0∈D
соответствует числовой ряд
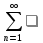 Un(x0).
Этот ряд может быть сходящимся или
расходящимся. Если для x0∈D
числовой ряд
Un(x0).
Этот ряд может быть сходящимся или
расходящимся. Если для x0∈D
числовой ряд
 Un(x0)
сходится, то говорят, чтo
функциональный ряд сходится в точке
x0,
и точку x0
наз. точкой
сходимости.Если
функциональный ряд сходится в каждой
точке x∈E⊂D,
то этот ряд наз. сходящимся
на множестве Е, а
множество Е
наз. областью сходимости ряда. Если
множествоЕ
пусто, то ряд расходится в каждой точке
множества D.
Un(x0)
сходится, то говорят, чтo
функциональный ряд сходится в точке
x0,
и точку x0
наз. точкой
сходимости.Если
функциональный ряд сходится в каждой
точке x∈E⊂D,
то этот ряд наз. сходящимся
на множестве Е, а
множество Е
наз. областью сходимости ряда. Если
множествоЕ
пусто, то ряд расходится в каждой точке
множества D.
Областью сходимостистепенного
ряда называется множество всех значений
переменной х , при которых соответствующий
числовой ряд сходится. Ряд вида а0+ а1х + а2х2+ … аnхn+ … = называетсястепенным рядом, а –
некот. числа, х – переменная.
называетсястепенным рядом, а –
некот. числа, х – переменная.
Коэффициентами степенного ряда называются числа а0, а1, … , аn.
Формулой Тейлорадля функцииf(x)
в окрестности точки х называется
многочлен Рn(х) =f(х0) +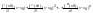 Остаточным
членом формулы Тейлора называется
последнее слагаемое в формуле Тейлора
Остаточным
членом формулы Тейлора называется
последнее слагаемое в формуле Тейлора
Rn(x)=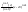 =f(x) –Pn(x)
=f(x) –Pn(x)
Т.о., многочлен Тейлора Рn(х) служит приближением функцииf(х). Оценкой этого приближения служит остаточный член формулы ТейлораRn(х).
Формулой Маклоренадля функцииf(х)
называется ее формула Тейлора при х0= 0:f(x)=f(0)
+
где с – некоторая точка из интервала (0, х).
