19 Экстремум функции. Необходимое усл.

Экстремум — макс. или миним. значение функции на заданном множестве. Точка, в которой достиг.экстремум, назыв. точкой экстремума. Если достигается минимум — точка экстр.называется точкой миним., а если максимум — точкой максимума.

Необходимый признак экстремума: ф-ияf(x) может иметьmaxиminтолько в тех точках, в которыхf`(x)=0 или не существует.

Для того чтобы функция y=f(x) имела экстремум в точке х₀, необходимо, чтобы ее произ-ная в этой точке = 0 или не сущ-ла, т.е. чтобы точка х₀была критической.

Достаточный признак: точка х₀является точкой экстремума, если ее производная в этой точке меняет знак:

- если с “+” на “-”, то х₀- т.max

- если с “-” на “+”, то х₀- т.min

20. Исследование функции.

Линия назыв. выпуклой, если она пересек.с любой своей секущей не более чем в 2х точ.

Линия наз-ся вогнутой, если она целиком лежит по 1 сторону от касательной, проведенной в любой ее точке.

Необходимый признак выпук. и вогнутости: если линия на интер. выпук., то ее f``(x)<=0; если линия на интер. вогн., то ееf``(x)>=0

Достаточный признак: если f``(x) всюду в интервале “-”, то линия в интервале выпуклая; еслиf``(x)>0, то линия вогнутая

Точка перегиба- точка, отделяющая выпуклый участок дуги от вогнутого.

Асимптота- прямая, к которой график ф-ции стремится, но никогда ее не пересекает.

Схема исслед. функции. Найти:- обл. определения ф-ции

-точки разрыва и интер, где ф-цияявл. непр.

-поведение ф-ции в окрестностях точки разрыва, вертикальной асимптоты

-т. пересечения графика с осями координат

-симметрия графика (чет./нечет)

-периодичность; -интервалы монотонности

-точки экстремума; -наибольшее и наим. значение -выпуклость, вогнутость

-точки перегиба

-поведение ф-ции в бесконечности, наклонная и горизонтальные асимптоты

-нанесение на график.

21. Первообр. Функции и неопр. Интеграл. Св-ва неопр. Инт. Таблица неопр. Интегр.

Функция F(x) наз-сяпервообразной ф-ции f(x) на определенном интервале, если

F'(x)=f(x) или dF(x)=f(x)dx.

Неопр. Интеграл- совок.всех первообр. для f(x), определенная на интерв. Х(∫f(x)dx=F(x)+c) Осн. теор. интегрирования: Если ф-ция f(x), опред. на интер. x , имеет 1 первообразную F(x), то она имеет бесконечное число первообразных, все они описываются выр-ем F(x)+c, где c-const. Свойства: 1. постоянную можно вынос.за знак интег. 2.интеграл суммы равен сумме интегралов 3.произв. от инт. равна подынтегр. функции 4.интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования.

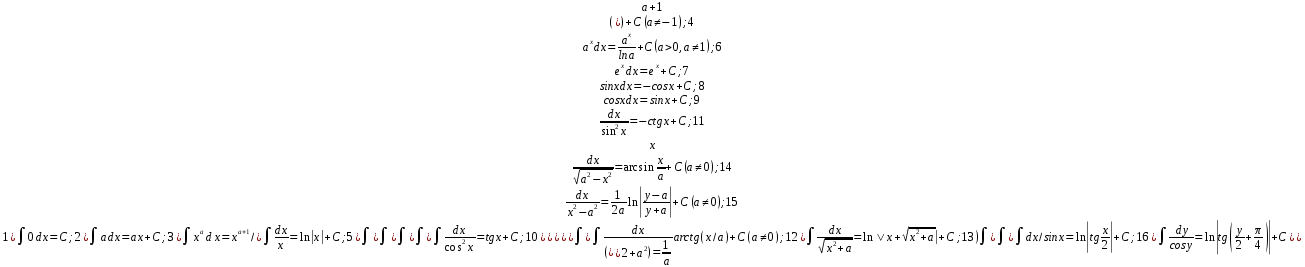
31. Линии уровня. Градиент.

Линией уровня функции называется множество точек из ее области определения, в которых функция принимает одно и то же фиксированное значение.

ЛУ– такая линия в плоскостиxиy, для кот.все значенияzодинаковы.z=x²+y²;y=√z-x² ;z=f(x,y).

Градиентомфункции f(x)называется вектор, указывающий направление наиболее быстрого возрастания функции, и, стало быть, ориентированный перпендикулярно линиям уровня.

Для линейной функции двух переменных линия уровня представляет собой прямую, перпендикулярную вектору с, который служит градиентом данной функции. Следовательно, если линия уровня определяется уравнением f(x)=c1x1+ c2x2 =const, то этот вектоp имеет вид 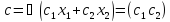и указывает направление возрастания функции.