7

Математическая статистика для психологов

Примеры решения типовых задач

Задача 1. Первичная обработка экспериментальных данных

При обследовании 50 членов семей рабочих и служащих установлено следующее количество членов семьи – признак :

5, 3, 2, 1, 4, 6, 3, 7, 9, 1, 3, 2, 5, 6, 8, 2, 5, 2, 3, 6, 8, 3, 4, 4, 5, 6, 5, 4, 7, 5, 6, 4, 8, 7, 4, 5, 7, 8, 6, 5, 7, 5, 6, 6, 7, 3, 4, 6, 5, 4.

1. Составьте дискретный вариационный ряд частот признака.

2. Постройте полигон распределения частот.

3. Определите средний размер (среднее число членов) семьи.

4. Охарактеризуйте вариативность размера семьи с помощью показателей вариации (дисперсии, среднего квадратического отклонения).

Объясните полученные результаты, сделайте выводы.

Решение

1) В данной задаче изучаемый признак является дискретным, так как размер семей не может отличаться друг от друга менее чем на одного человека. Следовательно, нужно построить дискретный вариационный ряд.

Расположим значения признака в порядке возрастания и найдем, сколько раз встречаются те или иные значения признака – частоты . Получим дискретный вариационный ряд частот признака:

	1	2	3	4	5	6	7	8	9
	2	4	6	8	10	9	6	4	1

2) Представим дискретный вариационный ряд графически, построив полигон частот.

1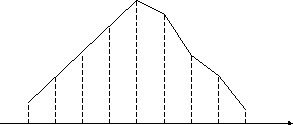0

9

8

7

6

5

4

3

2

1

0

0 1 2 3 4 5 6 7 8 9

3) Рассчитаем среднее число членов семьи в выборке по формуле выборочного среднего значения признака для сгруппированных данных. Получим:

.

Средний размер семьи в выборке около 5 человек.

4) Для расчета выборочной дисперсии используем формулу

.

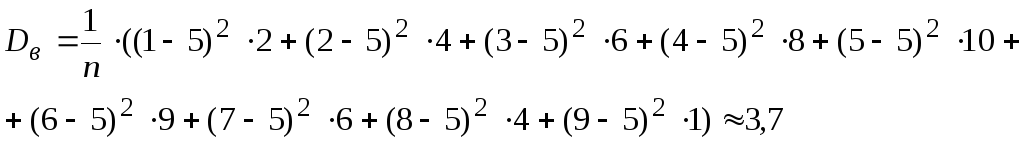
Дисперсия числа членов семьи равна 3,7 .

Найдем среднее квадратическое отклонение числа членов семьи: . Среднее квадратическое отклонение размера семьи равно 1,9 чел.

Задача 2. Нахождение доверительного интервала для математического ожидания

Найти доверительный интервал с надежностью 0,95 для оценки математического ожидания нормально распределенной случайной величины, если известны ее среднее квадратическое отклонение , выборочная средняя и объем выборки .

Решение

Воспользуемся формулой доверительного интервала неизвестного математического ожидания .

В случае малой выборки ()предельная ошибка выборки равна . Здесь находится по таблице распределения Стьюдента для степеней свободы и заданной доверительной вероятности .

В случае большой выборки () предельная ошибка выборки равна . Здесь находится по таблице значений функции Лапласа из условия .

В нашей задаче объем выборки велик (), поэтому значение найдем по таблице значений нормированной функции Лапласа с учетом того, что . Находим по таблице значение аргумента , которому соответствует значение функции .

Получим доверительный интервал, в котором с вероятностью 0,95 находится неизвестное математическое ожидание:

,

,

.

В интервал оцениваемое математическое ожидание попадает с заданной надежностью (вероятностью) 0,95.

Задача 3. Применение -критерия Стьюдента для двух независимых выборок

Преподаватель сопоставил изложение одной и той же темы в двух различных учебниках.

Работая в двух параллельных студенческих группах, он отобрал из них случайным образом две группы по 15 студентов в каждой и поручил им самостоятельно проработать эту тему: одной группе по первому учебнику, другой группе – по второму.

В конце эксперимента студентам был предложен тест на усвоение изученного материала. Результаты оценивались количеством правильных ответов (признак Х).

Были получены следующие данные:

в первой группе , , ;

во второй группе , , .

Значимы ли различия между средним количеством правильных ответов в группах?

Решение

Нулевую гипотезу : (о равенстве средних значений правильных ответов студентов двух групп) проверим на уровне значимости .

Альтернативная гипотеза вида : (о различии средних значений правильных ответов студентов двух групп) задает двустороннюю критическую область.

Выборки независимы, так как группы разные по составу. Применим критерий Стьюдента для независимых выборок.

Используем формулу для вычисления эмпирического значения критерия :

.

Критические точки -распределения Стьюдента для двусторонней критической области найдем по таблице при уровне значимости и числе степеней свободы . Получим .

Значит, правая критическая точка , а левая критическая точка . Область допустимых значений двустороннего -критерия есть симметричный интервал .

Значение находится внутри области допустимых значений , поэтому нет оснований для отклонения нулевой гипотезы о равенстве средних значений числа правильных ответов студентов двух групп. Различия между средним количеством правильных ответов в группах можно объяснить случайными причинами.

Задача 4. Применение -критерия Стьюдента для двух зависимых выборок.

Группа школьников () в течение летних каникул находилась в спортивном лагере. До и после сезона у них измерили жизненную емкость легких (признак ). До «эксперимента» (, мл):

3400, 3600, 3000, 3500, 2900, 3100, 3200, 3400, 3200, 3400.

После «эксперимента» (, мл):

3800, 3700,3300, 3600, 3100, 3200, 3200, 3300, 3500, 3600.

По результатам измерений нужно определить, значимо ли изменился этот показатель под влиянием интенсивных физических упражнений.

Решение

Вычислим средние значения жизненной емкости легких школьников до эксперимента

и после эксперимента

.

Как оказалось, средние значения двух зависимых выборок различаются. Определим, значимо ли это различие.

Нулевую гипотезу : (о равенстве средних значений жизненной емкости легких школьников) проверим на уровне значимости .

Альтернативная гипотеза : (о различии средних значений жизненной емкости легких школьников) задает двустороннюю критическую область.

Выбираем уровень значимости . Имеем две зависимые (связанные) выборки объема . Для удобства результаты вычислений проведем в таблице.

Таблица – Расчетная таблица критерия -Стьюдента для зависимых выборок

Номер школьника	Значения признака		Разности связанных пар результатов измерений	Квадраты отклонений
	до эксперимента ()	после эксперимента ()
1	3400	3800	- 400	1600
2	3600	3700	- 100	10000
3	3000	3300	- 300	90000
4	3500	3600	- 100	10000
5	2900	3100	- 200	40000
6	3100	3200	- 100	10000
7	3200	3200	0	0
8	3400	3300	100	10000
9	3200	3500	- 300	90000
10	3400	3600	- 200	40000
Сумма	32700	34300	- 1600	460000
Среднее				–

Найдем среднее арифметическое разностей :

.

Вычислим для разностей «исправленную» выборочную дисперсию (так как объем выборки меньше 30) по формуле , получим:

Вычислим выборочное среднее квадратическое отклонение и эмпирическое значение -критерия:

=.

Найдем по таблице критических значений Стьюдента для уровня значимости и числа степеней свободы .

Так как альтернативная гипотеза : , то критическая область двусторонняя. Строим ось значимости для -критерия Стьюдента, на которой отмечаем значение .

Критическая Критическая

область Область область

(различия значимы) допустимых (различия значимы)

значений

Значение попало в критическую область, поэтому показатели жизненной емкости легких школьников до и после спортивного лагеря значимо различаются с достоверностью 0,95.