Короткі теоретичні відомості

Довільну систему сил, прикладених до абсолютно твердого тіла, можна звести до однієї сили , яка дорівнює головному вектору системи сил і прикладена в центрі зведенняО, і однієї пари з моментом , який дорівнює головному моменту системи сил відносно центраО.

Головним вектором системи сил називається величина , що дорівнює геометричній сумі всіх сил системи;головним моментом системи сил відносно центра О називається величина , що дорівнює сумі моментів всіх сил відносно цього центраО:

; .

Звідси необхідні й достатні умови рівноваги будь-якої системи сил виражаються рівностями , тобто її головний вектор і головний момент відносно будь-якого центра дорівнюють нулю.

Оскільки вектор дорівнює нулю, то дорівнюють нулю його проекціїR_x і R_y, тобто повинні виконуватись рівності:

R_x=0, R_y=0 та ,

де М₀ – алгебраїчний момент сили, а О – будь-яка точка в площині дії сил.

Ці рівності будуть виконуватись тоді, коли:

.

Ці формули виражають аналітичні умови рівноваги: для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб суми проекцій всіх сил на кожну з двох координатних осей і сума їх моментів відносно будь-якого центра, що лежить у площині дії сил, дорівнювали нулю.

Одночасно ці рівності виражають умови рівноваги твердого тіла, яке перебуває під дією плоскої системи сил.

Методами статики можуть розв’язуватись задачі таких двох типів:

1) в яких відомі сили, прикладені до тіла, і вимагається з’ясувати, в якому положенні та при яких співвідношеннях між силами тіло буде перебувати у рівновазі;

2) в яких наперед відомо, що тіло перебуває у рівновазі, і треба з’ясувати, чому дорівнюють сили, що діють на тіло.

Реакції в’язей є величинами, наперед невідомими.

Всі розрахунки в задачі слід виконувати в загальному вигляді (аналітично),числа підставляються тільки в кінцеві результати. Це дає змогу проаналізувати здобуті результати.

Геометричним методом зручно користуватись, коли кількість сил (і заданих, і шуканих), прикладених до твердого тіла, дорівнює трьом.

Аналітичним методом користуються при будь-якій кількості сил. Для того, щоб дістати простіші рівняння необхідно:

а) складаючи рівняння проекцій сил, проводити координатну вісь перпендикулярно якій-небудь невідомій силі;

б) складаючи рівняння моментів, брати за центр моментів точку, де перетинаються більше невідомих сил.

Розв’язок багатьох задач статики зводиться до визначення реакцій опор. У техніці зустрічаються три типи опорних закріплень.

1. Рухома шарнірна опора А (рис.11). Реакція такої опори напрямлена по нормалі до поверхні, на яку спираються котки рухомої опори.

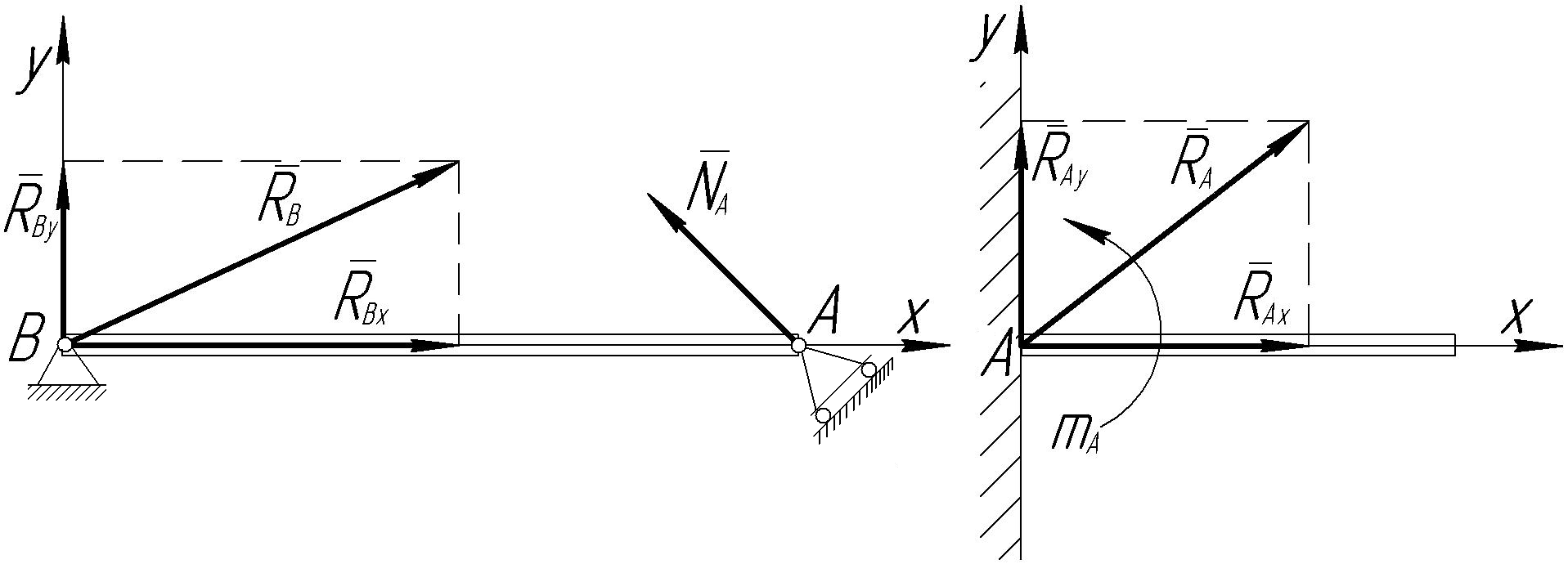
Рис.11 Рис.12

2. Нерухома шарнірна опора В (рис.11). Реакція такої опори проходить через вісь шарніра і може мати будь-який напрямок у площині креслення. Реакціюбудемо зображати її складовимиіпо напрямках координатних осей. Якщо визначимо їх, то:

.

3. Жорстке защемлення (нерухома защемляюча опора) (рис.12). Тут система реакцій зводиться до реакції , яка може бути розкладена ната, і пари з моментомm_A. Таким чином, для визначення реакції нерухомої защемляючої опори треба знайти три величини ,таm_A.