Приклади розв’язання задач

Задача 1. До вільного кінця А пружного горизонтального стержня, другий кінець В якого закріплений нерухомо, підвішений вантаж М вагою Р=40Н. Пружна сила стержня пропорційна стрілі прогину f. Статична стріла прогину стержня f_ст=0,04м. Визначити рівняння вантажу і період його коливань. Стержень прогинається на 0,01м під дією сили 10Н.

Розв’язання

На вантаж М, який розглянемо як матеріальну точку, діють сила ваги та сила пружності(рис. 42).

Нехай М₀ — початкове положення вантажу, при якому стержень не має прогину. Вісь Оx напрямимо вздовж вертикальної прямої, по якій рухається вантаж. Початок координат О оберемо в положенні статичної рівноваги так, що . У цьому положенні

,

де с – коефіцієнт пружності.

У

Рис. 42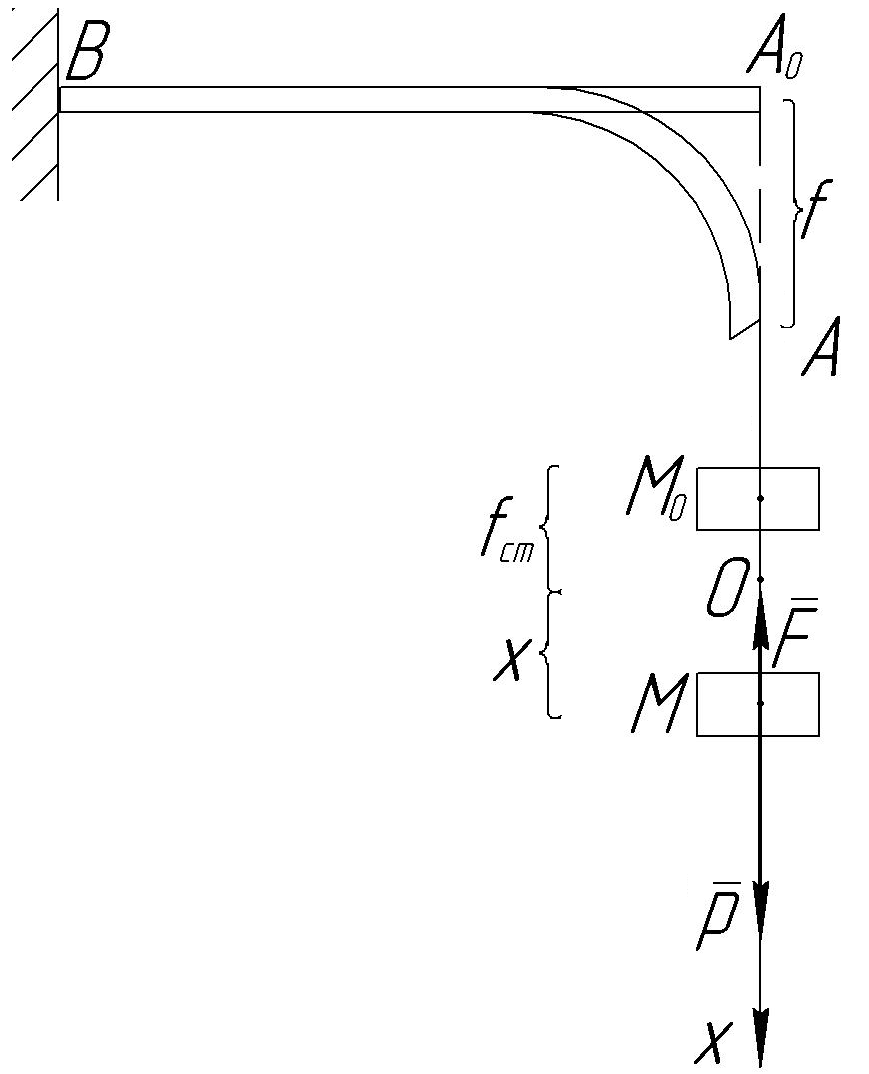

довільному положенніМ вантажу .

Складемо диференціальне рівняння руху вантажу:

,

звідки враховуючи, що P=сf_ст, дістанемо:

або ,

де .

Це лінійне однорідне диференціальне рівняння другого порядку має загальний розв’язок:

.

Сталі С₁ і С₂ визначаємо з початкових умов: при t=0: x₀=–f_ст, . Дістанемо:С₁=–f_ст, С₂=0.

Тоді закон коливального руху вантажу буде:

або враховуючи, що f_ст=0,04м, с=10Н/м, , рівняння руху вантажу набуде вигляду:

.

Період коливань:

.

Задача 2. Тіло масою m=2кг, підвішене на пружині, відхиляють вниз із положення рівноваги x₀=0,04м і відпускають, надаючи йому швидкість , напрямлену вгору. Відомо, що силаF=12Н збільшує довжину пружини на 0,03м. Знайти основні характеристики і кінематичний закон руху тіла.

Розв’язання

Очевидно, що тіло здійснює вільні гармонійні прямолінійні коливання. Тоді закон його руху має вигляд:

.

Знайдемо характеристики руху тіла: A – амплітуду, T – період, k – кругову частоту, – початкову фазу коливань.

Знаючи, що (дес — коефіцієнт жорсткості пружини), визначимо с:

Тоді:

(с^–1);

(с);

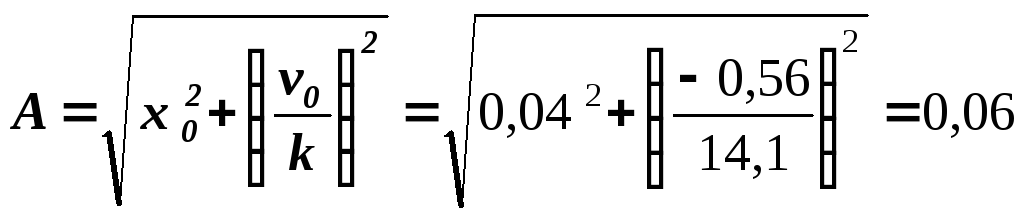(м);

звідки

.

Кінематичний закон руху тіла:

(м).

Задача 3.Тверде тіло масою m=0,4кг підвішене на пружині, верхній кінець якої здійснює гармонійні коливання вздовж вертикальної прямої за законом , при цьомуa=0,02м, р=7с^–1. Під дією сили, яка дорівнює 0,4Н, пружина видовжується на 0,01м. Визначити закон вимушених коливань тіла.

Розв’язання

Т

Рис. 43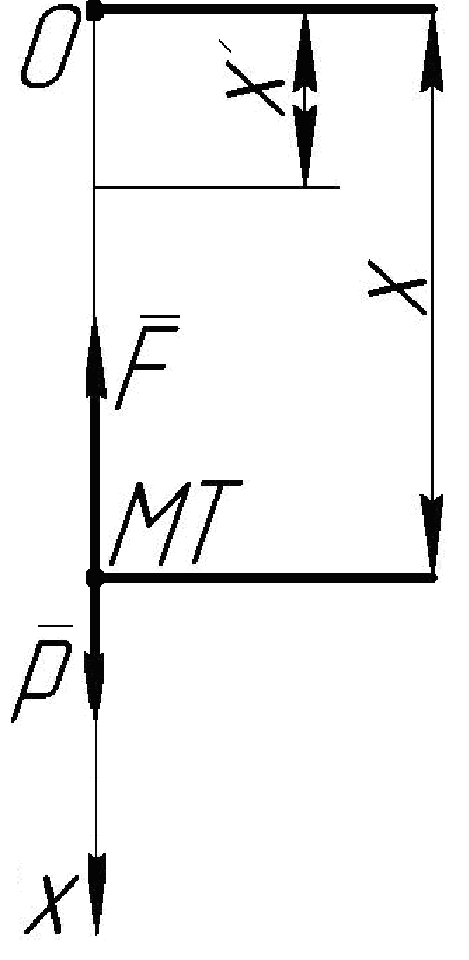

іло розглянемо як матеріальну точку. Координатну вісь напрямимо вздовж прямої руху матеріальної точки вертикально вниз (рис. 43). Початок координат розмістимо в положенні статичної рівноваги матеріальної точки. Зобразимо сили, які діють на матеріальну точку: силу пружності пружиниі збуджуючу силу (Р_х= сх= с аsin pt).

Складемо диференціальне рівняння руху матеріальної точки в проекції на вісь Ох:

. (1)

Позначимо ,, тоді рівняння (1) набуде вигляду:

. (2)

З урахуванням початкових умов:

,

тоді k=10c^-1,

.

Оскільки , амплітуда вимушених коливань:

.

Тоді закон руху тіла має вигляд:

.

Питання для самоконтролю

1. Вивести диференціальне рівняння вільних коливань точки. Його загальні розв’язки в двох виглядах.

2. Дати кінематичну інтерпретацію всім характеристикам вільних коливань точки.

3. Що називається амплітудою коливань, фазою, початковою фазою, круговою частотою, частотою та періодом коливань?

4. Як визначаються сталі інтегрування А та α?

5. Як впливає стала сила на характер вільних коливань точки?

6. Коли виникають вимушені коливання матеріальної точки?

7. Записати диференціальне рівняння вимушених коливань точки та його загальний розв’язок.

8. Дати пояснення явищу резонансу.