
- •Міністерство освіти і науки України
- •Модуль «статика абсолютно твердого тіла»
- •Короткі теоретичні відомості
- •Приклади розв’язання задач
- •Розв’язання
- •Розв’язання
- •Питання для самоконтролю
- •Задачі для самостійного розв’язання
- •До задачі 1.1
- •До задачі 1.2
- •До задачі 1.3
- •До задачі 1.5
- •До задачі 1.6
- •До задачі 1.7
- •До задачі 1.10
- •До задачі 1.12
- •До задачі 1.13
- •Практичне заняття №2 Тема: Система паралельних сил. Центр ваги Програмні питання
- •Література
- •Короткі теоретичні відомості
- •Приклади розв’язання задач
- •Розв’язання
- •Розв’язання
- •Питання для самоконтролю
- •Задачі для самостійного розв’язання
- •До задачі 2.2
- •До задачі 2.5
- •До задачі 2.7
- •До задачі 2.8
- •До задачі 2.9
- •Практичне заняття №3 Тема: Довільна плоска система сил Програмні питання
- •Література
- •Короткі теоретичні відомості
- •Приклади розв’язання задач
- •Розв’язання
- •Розв’язання
- •Питання для самоконтролю
- •До задачі 3.10
- •Короткі теоретичні відомості
- •Приклади розв’язання задач
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Питання для самоконтролю
- •Задачі для самостійного розв’язання
- •До задачі 4.3
- •До задачі 4.7
- •Модуль «кінематика матеріальної точки та твердого тіла»
- •Короткі теоретичні відомості
- •Приклади розв’язання задач
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Питання для самоконтролю
- •Задачі для самостійного розв’язання
- •До задачі 5.6
- •Короткі теоретичні відомості
- •Приклади розв’язання задач
- •Розв’язання
- •Розв’язання
- •Питання для самоконтролю
- •Задачі для самостійного розв’язання
- •До задачі 6.1
- •Практичне заняття №7 Тема: Поступальний та обертальний рух твердого тіла навколо нерухомої осі Програмні запитання
- •Література
- •Короткі теоретичні відомості
- •Приклади розв’язання задач
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Питання для самоконтролю
- •Задачі для самостійного розв’язання
- •До задачі 7.9
- •Практичне заняття №8 Тема: Плоскопаралельний рух твердого тіла. Складний рух точки та тіла Програмні питання
- •Література
- •Короткі теоретичні відомості
- •Приклади розв’язання задач
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Питання для самоконтролю
- •Задачі для самостійного розв’язання
- •До задачі 8.1
- •До задачі 8.2
- •До задачі 8.3
- •До задачі 8.6
- •До задачі 8.7
- •До задачі 8.9
- •Модуль «динаміка матеріальної точки та механічної системи»
- •Короткі теоретичні відомості
- •Приклади розв’язання задач
- •Розв’язання
- •Розв’язання
- •Питання для самоконтролю
- •Задачі для самостійного розв’язання
- •Практичне заняття №10 Тема: Розв’язання другої задачі динаміки матеріальної точки Програмні питання
- •Література
- •Короткі теоретичні відомості
- •Приклади розв’язання задач
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Питання для самоконтролю
- •Задачі для самостійного розв’язання
- •До задачі 10.6
- •Практичне заняття №11 Тема: Прямолінійні коливання матеріальної точки Програмні питання
- •Література
- •Короткі теоретичні відомості
- •Приклади розв’язання задач
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Питання для самоконтролю
- •Задачі для самостійного розв’язання
- •До задачі 11.1
- •До задачі 11.7
- •Практичне заняття №12 Тема: Теореми про зміну кількості руху матеріальної точки та механічної системи. Теореми про зміну моменту кількості руху матеріальної точки та системи Програмні питання
- •Література
- •Короткі теоретичні відомості
- •Приклади розв’язання задач
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Питання для самоконтролю
- •Задачі для самостійного розв’язання
- •До задачі 12.5
- •До задачі 12.8
- •До задачі 12.9
- •Практичне заняття №13 Тема: Теореми про зміну кінетичної енергії матеріальної точки та механічної системи. Теорема про рух центра мас системи Програмні питання
- •Література
- •Короткі теоретичні відомості
- •Приклади розв’язання задач
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Питання для самоконтролю
- •Задачі для самостійного розв’язання
- •До задачі 13.7
- •До задачі 13.8
- •До задачі 13.10
- •До задачі 13.11
- •Тестові завдання Модуль «Статика абсолютно твердого тіла»
- •Модуль «Кінематика матеріальної точки та твердого тіла»
- •Модуль «Динаміка матеріальної точки та механічної системи»
- •Контрольні завдання Модуль «Статика абсолютно твердого тіла»
- •Модуль «Кінематика матеріальної точки та твердого тіла»
- •Модуль «Динаміка матеріальної точки та механічної системи»
- •Питання до підсумкового контролю Модуль «Статика абсолютно твердого тіла»
- •Модуль «Кінематика матеріальної точки та твердого тіла»
- •Модуль «Динаміка матеріальної точки та механічної системи»
- •Список рекомендованої літератури
- •Додатки
- •Формули алгебри і тригонометрії
- •Спеціальні значення тригонометричних функцій
- •Одиниці механічних величин у системі сі
- •Латинський алфавіт
- •Грецький алфавіт
Короткі теоретичні відомості
Динамікою називається розділ механіки, в якому рух матеріальних тіл вивчається з урахуванням сил, що діють на них.
У кінематиці розглядаються три способи задання руху точки: векторний, координатний і натуральний. У зв’язку з цим, базуючись на другому законі динаміки, виводяться диференціальні рівняння руху матеріальної точки в трьох формах: векторній, координатній та натуральній.
Рівняння у векторній формі. Із кінематики відомо, що рівняння руху точки у векторній формі має вигляд:
![]() ,
,
де
![]() – радіус-вектор, який визначає положення
точки в будь-який момент часу.
– радіус-вектор, який визначає положення
точки в будь-який момент часу.
Прискорення точки дорівнює:
![]()
Підставляючи це значення у формулу для визначення сили, маємо:
![]() .
.
Ця рівність називається диференціальним рівнянням руху матеріальної точки у векторній формі. Якщо на точку діє декілька сил, то:
![]()
Рівняння в координатній формі. Рух точки в прямокутних декартових координатах задається рівняннями:
![]()
Знайдемо рівняння, які пов’язують координати x, y, z цієї точки і силу (або сили), що діє на неї. Ці рівняння дає другий закон динаміки.
Розглянемо
матеріальну точку, яка рухається під
дією сил
![]() ,
,![]() ,
...,
,
...,![]() по відношенню до інерціальної системи
відлікуOxyz.
Проектуючи обидві частини рівності
по відношенню до інерціальної системи
відлікуOxyz.
Проектуючи обидві частини рівності
![]() на осіx,
y,
z
і враховуючи, що
на осіx,
y,
z
і враховуючи, що
![]() ,
,![]() та
та![]() ,
дістаємо:
,
дістаємо:
![]()
або, позначаючи другі похідні за часом двома штрихами, маємо:
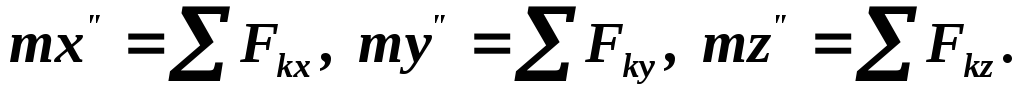
Це і є диференціальні рівняння руху точки в прямокутних декартових координатах.
Оскільки діючі на точку сили можуть залежати від часу t, від координат x, y, z і від швидкості, тобто vx=x', vy=y', vz=z', то в загальному випадку права частина кожного рівняння може бути функцією всіх цих змінних, тобто, t, x, y, z, x', y', z' одночасно.
Рівняння
в натуральній формі.
Для того щоб дістати ці рівняння,
спроектуємо обидві частини рівності
![]() на осі натурального тригранникаМτnb,
тобто на дотичну Мτ
до траєкторії точки, головну нормаль
Мn,
напрямлену в бік угнутості траєкторії,
і бінормаль Мb.
Тоді, враховуючи, що:
на осі натурального тригранникаМτnb,
тобто на дотичну Мτ
до траєкторії точки, головну нормаль
Мn,
напрямлену в бік угнутості траєкторії,
і бінормаль Мb.
Тоді, враховуючи, що:
![]()
дістаємо:
![]()
Ці
рівняння, де
![]() ,
єдиференціальними
рівняннями руху точки в натуральній
формі.
,
єдиференціальними
рівняннями руху точки в натуральній
формі.
На основі диференціальних рівнянь руху матеріальної точки можна розв’язати такі основні задачі її динаміки:
1) перша задача (пряма): визначення величини і напрямку сили, яка діє на точку, знаючи масу точки і закон її руху;
2) друга задача (обернена, основна): знаходження закону руху точки, якщо відомі маса точки і сили, що діють на неї.
Розглянемо загальну методику розв’язання першої задачі динаміки точки. Воно здійснюється у такій послідовності:
1) диференціювання двічі за часом функцій, які виражають кінематичний закон руху точки;
2)підставлення результатів диференціювання у відповідні диференціальні рівняння й отримання з них значень проекцій сил;
3) визначення модуля сили і косинусів кутів, які визначають напрямок сили (за формулами, відомими із векторної алгебри).
Приклади розв’язання задач
Задача 1. Матеріальна точка m=1кг здійснює рух згідно рівнянь: x=2t2+3, y=t3+1, z=t2–2, причому координати точки виражені в метрах, час – в секундах. Визначити величину та напрямок сили, яка діє на точку в момент часу t=1c.
