З

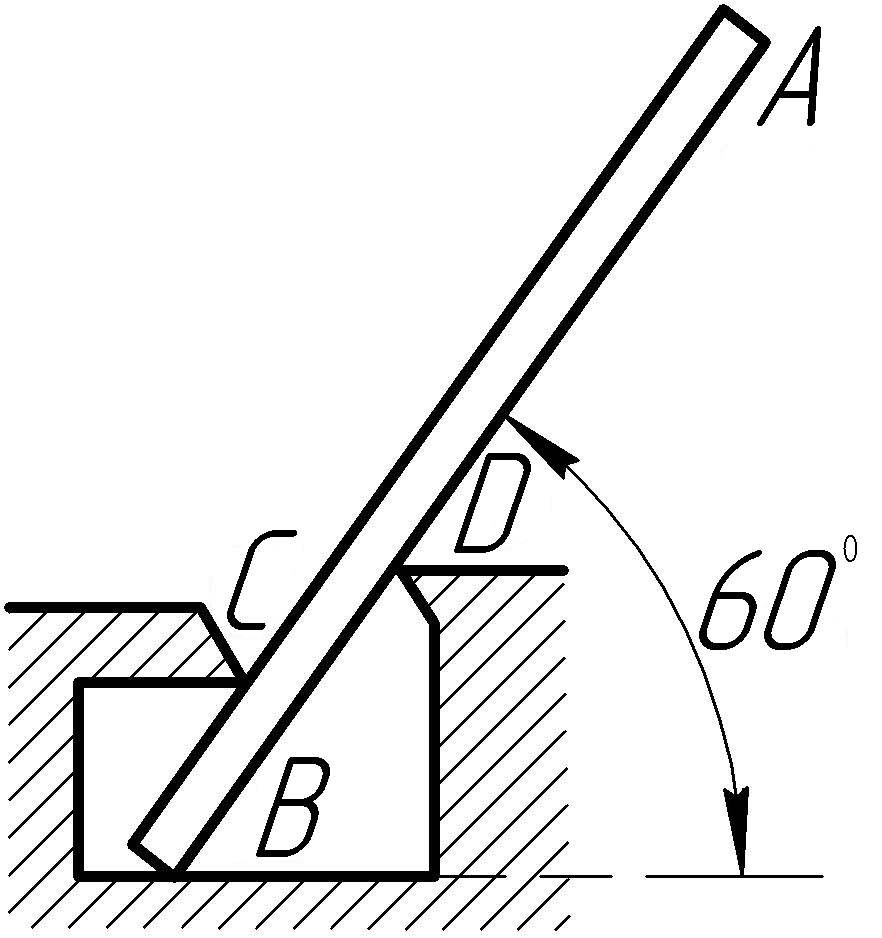
До задачі 3.10

адача 3.10.Однорідна балка АВ вагою 200 Н спирається на гладеньку горизонтальну підлогу в точці В під кутом і, крім цього, підтримується двома опорамиС і D. Визначити реакції опор в точках В, С і D, якщо довжина АВ=3 м; ВС=CD=0,5 м.

Відповідь: R_В=200Н, R_С=300Н, R_D=300Н.

Практичне заняття №4

Тема: Просторова система сил

Програмні питання

Просторова система сил. Момент сили відносно осі. Послідовність його визначення, часткові випадки. Обчислення головного вектора і головного моменту просторової системи сил. Зведення просторової системи сил до найпростішого вигляду. Рівновага довільної просторової системи сил. Випадки збіжних і паралельних сил.

Література

1. Курок В.П. Технічна механіка. Курс лекцій: навч. посіб. для студ. вищих навч. закл. – К.: Пед. преса, 2007. – 272с., л.9.

2. Тарг С.М. Краткий курс теоретической механики. – М.: Высшая школа, 1986. – 416с., §§28 – 30.

3. Никитин Е.М. Краткий курс теоретической механики. – М.: Наука, 1983. – 400с., §§32 – 36.

4. Цасюк В.В. Теоретична механіка: Навчальний посібник. – К.: Центр навчальної літератури, 2004. – 402с., §§4.1 – 4.8.

5. Мещерский И.В. Сборник задач по теоретической механике. – М.: Наука, 1986. – 448с.

Короткі теоретичні відомості

Проекція вектора , тобто моменту сили відносно центра О, на яку-небудь вісь z, що проходить через цей центр (рис. 15), називається моментом сили відносно осі z, тобто

або ,

де – момент силивідносно осіz, γ – кут між вектором і віссюz.

І

Рис.15

з означення виходить, що, як проекція вектора на вісь,величина алгебраїчна. Знак визначається так само, як і знак проекції будь-якого вектора, у нашому випадку>0.

Знайдемо ще один вираз для визначення цієї величини. Для цього через довільну точку О₁ осі z (див. рис.15) проведемо площину (xy), перпендикулярну цій осі, й спроектуємо ∆ОАВ на цю площину. Оскільки вектор перпендикулярний площиніОАВ, а вісь z перпендикулярна ΔО₁А₁В₁, то кут γ, як кут між нормалями до цих площин, буде кутом між цими площинами. Тоді:

або .

Отже, момент сили відносно осі z дорівнює алгебраїчному моменту проекції цієї сили на площину, перпендикулярну осі z, взятому відносно точки О₁ перетину осі з цією площиною.

Ц

Рис.16

е є друге означення моменту сили відносно осі.

Момент сили відносно осі буде мати знак плюс, коли з додатного кінця осі поворот, що прагне здійснити сила , бачиться проти ходу годинникової стрілки, а знак мінус – за ходом годинникової стрілки.

Послідовність обчислення моменту сили відносно осі (рис.16):

1) необхідно провести площину (xy), перпендикулярну осі z;

2) спроектувати силу на цю площину і знайти величинуF_xy;

3) опустити із точки перетину О осі з площиною перпендикуляр на лінію дії і знайти його довжинуh;

4) обчислити добуток F_xy·h;

5) визначити знак моменту.

Поодинокі випадки:

1) якщо сила паралельна осі, то її момент відносно осі дорівнює нулю (оскільки F_xy=0);

2) якщо лінія дії сили перетинає вісь, то її момент відносно осі також дорівнює нулю ( оскільки h=0) ;

3) якщо сила перпендикулярна осі, то її момент відносно цієї осі дорівнює взятому з відповідним знаком добутку модуля сили на відстань між лінією дії сили і віссю.

Поєднуючи пункти 1 і 2, відзначимо, що момент сили відносно осі дорівнює нулю, якщо сила і вісь лежать в одній площині.

Необхідні й достатні умови рівноваги будь-якої системи сил виражаються рівностями ,. Але векторитадорівнюють нулю тільки тоді, колиі, тобто коли:

Таким чином, для рівноваги довільної просторової системи сил необхідно і достатньо, щоб суми проекцій всіх сил на кожну з трьох координатних осей і алгебраїчні суми їх моментів відносно цих осей дорівнювали нулю.

Випадок збіжних сил. Для рівноваги просторової системи збіжних сил має виконуватись рівність . Аналітично модуль головного вектора визначається за формулою:

Оскільки під коренем стоїть сума додатних складових, то R може дорівнювати нулю тільки тоді, коли одночасно R_x=0, R_y=0, R_z=0,тобто коли сили, що діють на тіло, будуть задовольняти рівності:

Ц

Рис. 17

і рівності і виражають умови рівноваги системи збіжних сил в аналітичній формі:для рівноваги просторової системи збіжних сил необхідно і достатньо, щоб алгебраїчні суми проекцій цих сил на кожну з трьох координатних осей дорівнювали нулю.

Випадок паралельних сил. Якщо всі сили, що діють на тіло, паралельні одна одній, можна обрати координатні осі таким чином, щоб вісь z була паралельна силам (рис.17). Тоді проекції кожної із сил на осі x та y і їх моменти відносно осі z будуть дорівнювати О, тому будемо мати тільки три умови:

Отже, для рівноваги просторової системи паралельних сил необхідно і достатньо, щоб алгебраїчна сума проекцій всіх сил на вісь, паралельну силам, і алгебраїчні суми їх моментів відносно двох інших координатних осей дорівнювали нулю.