2.3.2 Спектр сигналов с угловой модуляцией

Будем изучать модулированные радиосигналы, которые получаются за счёт того, что в несущем гармоническом колебании 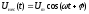передаваемое сообщение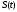изменяет либо частоту, либо начальную фазу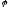; амплитуда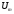остаётся неизменной. Поскольку аргумент гармонического колебания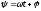, называемый полной фазой, определяет текущее значение фазового угла, такие сигналы получили название сигналов с угловой модуляцией.

Однотональные сигналы с угловой модуляцией. Анализ ФМ- и ЧМ-сигналов с математической точки зрения гораздо сложнее, чем исследование АМ-колебаний. Поэтому мы будем рассматривать простейшие однотональные сигналы.

В случае однотонального ЧМ-сигнала мгновенная частота:

,

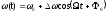где - девиация частоты сигнала.

Полная фаза такого сигнала

,

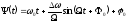где 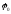– некоторый постоянный фазовый угол.

Величина

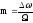(2.39)

называется индексом однотональной угловой модуляции.

Для краткости положим, что неизменные во времени фазовые углы 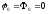, и выразим мгновенное значение ЧМ-сигнала в виде:

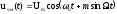(2.40)

Аналитическая форма записи однотонального ФМ-сигнала будет аналогичной. Однако нужно иметь в виду следующее: ЧМ- и ФМ-сигналы ведут себя по-разному при изменении частоты модуляции и амплитуды модулирующего сигнала, кроме того при Ф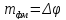М , а при ЧМ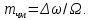

Спектральное разложение ЧМ- и ФМ-сигналов при малых индексах модуляции. Задачу о представлении сигналов с угловой модуляцией посредством суммы гармонических колебаний несложно решить в случае, когда 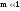. Для этого преобразуем формулу (2.40) следующим образом:

(2.41)

Поскольку индекс угловой модуляции мал, воспользуемся приближёнными равенствами:

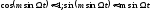
На основании этого из равенства (2.41) получаем:

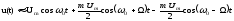(2.42)

Таким образом, показано, что при 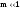в спектре сигнала с угловой модуляцией, содержатся несущие колебания и две боковые составляющие (верхняя и нижняя) на частотах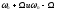. Индексm играет здесь такую же роль как коэффициент М при АМ. Однако можно обнаружить и существенное различие спектров АМ-сигнала и колебания с угловой модуляцией.

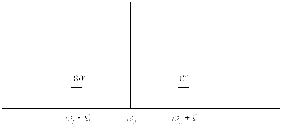
Спектральная диаграмма сигнала с угловой модуляцией при .

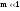Для спектральной диаграммы, построенной по формуле (2.42) характерно то, что нижнее боковое колебание имеет дополнительный фазовый сдвиг на 180 градусов. При значениях m=0.5-1 появляется вторая пара гармонических колебаний с боковыми частотами 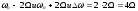, затем третья пара и так далее. Возникновение новых спектральных составляющих приводит к перераспределению энергии по спектру.

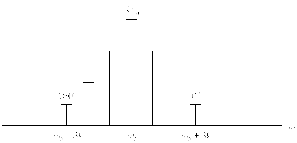
С ростом m амплитуда боковых составляющих увеличивается, в то время как амплитуда несущего колебания уменьшается.

Спектр сигнала с угловой модуляцией при произвольном значении индекса m. Для простейшего случая однотонального ЧМ- и ФМ-сигнала можно найти общее выражение спектра, справедливое при любом значении индекса модуляции m.

Математическая модель ЧМ- или ФМ-сигнала с любым значением индекса модуляции:

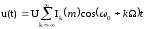(2.43)

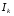(m) – функция Бесселя k- того порядка от аргумента m.

Спектр однотонального сигнала с угловой модуляцией в общем случае содержит бесконечное число составляющих, частоты которых равны 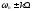; амплитуды этих составляющих пропорциональные значениям.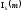

В теории функций Бесселя доказывается, что функции с положительными и отрицательными индексами связаны между собой соотношением:

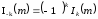
Поэтому начальные фазы боковых колебаний с частотами 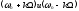совпадают, еслиk- чётное число, и отличаются на 180 градусов, если k- нечётное. С ростом индекса модуляции расширяется полоса частот, занимаемая сигналом. Обычно полагают, что допустимо пренебречь всеми спектральными составляющими с номерами 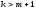. Отсюда следует оценка практической ширины спектра сигнала с угловой модуляцией.

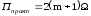(2.44)

Как правило, реальные ЧМ- и ФМ-сигналы характеризуются условием 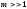. В этом случае

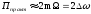(2.45)

Таким образом, сигнал с угловой модуляцией занимает полосу частот, приблизительно равную удвоенной девиации частоты.

Для передачи АМ-сигнала требуется полоса частот, равная , то есть вm раз меньшая. Большая широкополосность ЧМ- и ФМ-сигналов обуславливает их гораздо более высокую помехоустойчивость по сравнению с АМ-сигналами.

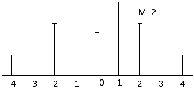
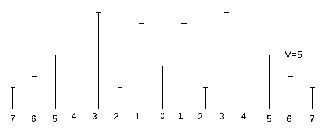
Спектральные диаграммы сигнала с угловой модуляцией при двух значениях индекса m (амплитуды представлены в относительном масштабе).