1.2 Ортогональные сигналы. Ортонормированный базис. Обобщенный ряд Фурье

Ортогональные сигналы. Введём понятие скалярного произведения элементов линейного пространства. Скалярное произведение вещественных сигналов и: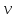

Скалярное произведение обладает следующими свойствами:

1. 

2. 

3. , где - вещественное число

4. 

5. - справедливо неравенство Коши-Буняковского.

Линейное пространство с таким скалярным произведением, содержащее в себе все предельные точки любых сходящихся последовательностей векторов из этого пространства называется вещественным Гильбертовым пространством H.

Если сигналы принимают комплексные значения, то можно определить комплексное Гильбертово пространство.

Если сигналы комплексные, то скалярное произведение:

Два сигнала иназывают ортогональными, если их скалярное произведение, а значит, и взаимная энергия равны нулю:

.

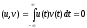Ортонормированный базис.Обобщенный ряд Фурье. Предположим, что на отрезке задана бесконечная система функций, ортогональных друг другу и обладающих единичными нормами:

1, если

0, если

Говорят, что при этом в пространстве сигналов задан ортонормированный базис. Разложим произвольный сигнал в ряд:

(1.1)

Такое представление называется обобщённым рядом Фурье сигнала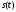в выбранном базисе.

Коэффициенты данного ряда находят следующим образом. Возьмём базисную функцию с произвольным номером, умножим на неё обе части равенства (1.1) и затем проинтегрируем результаты по времени:

(1.2)

Ввиду ортонормированности базиса по определению в правой части равенства (1.2) останется только член суммы с номером , поэтому:

(1.3)

Рассмотрим некоторый сигнал, 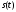, разложенный в ряд по ортонормированной базисной системе и вычислим его энергию, непосредственно подставив этот ряд в соответствующий интеграл:

Поскольку базисная система функций ортонормирована, в сумме окажутся отличными от нуля только члены с номерами . Отсюда получается замечательный результат, который называется равенством Парсеваля:

(1.4)

Смысл этой формулы: энергия сигнала есть сумма энергий всех компонент, из которых складывается обобщённый ряд Фурье.

Раздел 2. Основы спектрального анализа сигналов

1. 2.1 Теоремы о спектрах

Как известно спектральная плотность и сигнал связаны между собой парой преобразований Фурье:

(2.1)

(2.2)

Все свойства спектральной плотности объединены в основных теоремах о спектрах.

I.Свойство линейности.

Если имеется некоторая совокупность сигналов причём,…, то взвешенная сумма сигналов преобразуется по Фурье следующим образом:

(2.3)

Здесь - произвольные числовые коэффициенты.

II. Теорема о сдвигах.

Предположим, что для сигнала известно соответствие. Рассмотрим такой же сигнал, но возникающий насекунд позднее. Принимая точкуза новое начало отсчёта времени, обозначим этот смещённый сигнал как. Введём замену переменной:. Тогда,

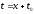(2.4)

Модуль комплексного числа при любых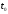равен 1, поэтому амплитуды элементарных гармонических составляющих, из которых складывается сигнал, не зависят от его положения на оси времени. Информация об этой характеристике сигнала заключена фазовом спектре.

III. Теорема масштабов.

Предположим, что исходный сигнал подвергнут изменению масштаба времени. Это означает, что роль временииграет новая независимая переменная(- некоторое вещественное число.) Если> 1, то происходит “ сжатие” исходного сигнала; если же 0<<1, то сигнал “растягивается” во времени. Если, то :

Произведём замену переменной , тогда, откуда следует:

(2.5)

При сжатии сигнала в раз на временной оси во столько же раз расширяется его спектр на оси частот. Модуль спектральной плотности при этом уменьшается враз.

Очевидно, что при растягивании сигнала во времени ( т.е. при <1) имеет место сужение спектра и увеличение модуля спектральной плотности.

IV.Теорема о спектре производной и неопределённого интеграла.

Пусть сигнал и его спектральная плоскостьзаданы. Будем изучать новый сигнали поставим цель найти его спектральную плотность.

По определению:

Преобразование Фурье – линейная операция, значит, равенство (2.3) справедливо и по отношению к спектральным плотностям. Получаем по теореме о сдвигах:

(2.6)

Представляя экспоненциальную функцию рядом Тейлора:

подставляя этот ряд в (2.6) и ограничиваясь первыми двумя членами ряда, находим

(2.7)

Итак, дифференцирование сигнала по времени эквивалентно простой алгебраической операции умножения спектральной плотности на множитель 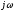. Поэтому говорят, что мнимое числоявляется оператором дифференцирования, действующим в частотной области.

Вторая часть теоремы. Рассмотренная функция является неопределённым интегралом по отношению к функции. Интеграл это есть, значит- его спектральная плотность, аиз формулы (2.7) равна:

(2.8)

Таким образом, множитель служит оператором интегрирования в частотной области.

V. Теорема о свёртке.

Как известно, при суммировании сигналов их спектры складываются. Однако спектр произведения сигналов не равен произведению спектров, а выражается некоторым специальным интегральным соотношением между спектрами сомножителей.

Пусть и- два сигнала, для которых известны соответствия,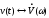. Образуем произведение этих сигналов:и вычислим его спектральную плотность. По общему правилу:

(2.9)

Применив обратное преобразование Фурье, выразим сигнал 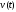через его спектральную плотность и подставим результат в (2.9):

Изменив порядок интегрирования, будем иметь:

откуда:

(2.10)

Интеграл, стоящий в правой части называют свёрткой функци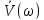й и. Символически операция свёртки обозначается как *

Таким образом, спектральная плотность произведения двух сигналов с точностью до постоянного числового множителя равна свёртке спектральных плотностей сомножителей:

(2.11)

Операция свёртки коммутативна, т.е. допускает изменения порядка следования преобразуемых функций:

Теорема о свёртке может быть обращена: если спектральная плотность некоторого сигнала представляется в виде произведения , причём

и , то сигналявляется свёрткой сигналови, но уже не в частотной, а во временной области:

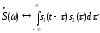(2.12)

VI.Теорема Планшереля

Пусть два сигнала и, в общем случае комплексные, определены своими обратными преобразованиями Фурье:

,

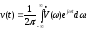
Найдём скалярное произведение этих сигналов, выразив один из них, например , через его спектральную плотность:

Здесь внутренний интеграл представляет собой спектральную плотность сигналапоэтому:

(2.13)

Скалярное произведение двух сигналов с точностью до коэффициента пропорционально скалярному произведению их спектральных плотностей.

2.2. δ-функция и ее свойства.

Многие задачи радиотехники, например вычисление отклика физической системы на известное входное воздействие, требуют специфической формы представления сигналов. Необходимо не только располагать информацией о мгновенном значении сигнала, но и знать его поведение на всей временной оси как «в прошлом», так и «в будущем».

Принцип динамического представления состоит в следующем. Реальный сигнал приближенно представляется суммой некоторых элементарных сигналов, возникающих в последовательные моменты времени. Если теперь устремить к нулю длительность отдельных элементарных сигналов, то, естественно в пределе будет получено точное представление исходного сигнала

Широкое применение нашли два способа динамического представления. Согласно первому из них в качестве элементарных сигналов используются ступенчатые функции, возникающие через равные промежутки времени ∆

В нашем курсе будет постоянно использоваться аппарат дельта - функций. Дельта- функция как раз и является математической моделью короткого внешнего воздействия с единичным импульсом (площадью).

Рассмотрим импульсный сигнал прямоугольной формы, заданный следующим образом:

υ

где: - функция включения: νξ

При любом выборе параметра ξ площадь этого

импульса равна единице: t

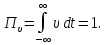
0

Например, если υ – напряжение, то В·с.

Пусть теперь величина ξ стремится к нулю. δ (t-t₀ )

Импульс, сокращаясь по длительности, сохраняет

свою площадь, поэтому его высота должна

неограниченно возрастать. Предел последовательности

таких функций при носит названиедельта- функции t

или функции Дирака :

t₀

Дельта-функция интересный математический Графическое изобра-

объект. Будучи равной нулю всюду, за исключением жение δ-функции

точки (принято говорить, что она сосредото-

чена в этой точке), δ- функция тем не менее обладает единичным интегралом:

т.е. площадь, ограниченная дельта - функцией, равна единице.

Полезным для расчетов является фильтрующее свойство δ-функции, которое заключается в следующем. Интеграл от произведения от некоторой функции u(t) на δ-функцию равен значению этой функции при t, для которого δ(t) ≠ 0.

Например:

Согласно (2.1) спектральную плотность δ-функции можно представить в виде:

Можно представить также в виде обратного преобразования Фурье от=:

По аналогии с выражением (2.15) можно представить δ-функцию в частотной области:

Используя (2.16) можно получить представление спектральной плотности для ряда неинтегрируемых сигналов.

1. Спектральная плотность постоянного по времени сигнала

2. Спектральная плотность комплексного экспоненциального сигнала

=2

3. Спектральная плотность гармонических колебаний:

,

,

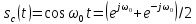4. Спектральная плотность произвольного периодического сигнала

5. Спектральная плотность функции включения

6. Спектральная плотность радиоимпульса

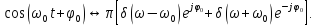
Применяя теорему о свертке и фильтрующее свойство δ-функции, получим: