Раздел 11. Принципы оптимальной обработки сигналов на фоне помех

11.1. Задача оптимального приёма дискретных сообщений

В дискретных системах связи сообщение представляет собой набор (или последовательность) элементов и каждый элемент сообщенияпередаётся соответствующим сигналом,. В приёмном устройстве системы связи по принятому колебаниюдолжен восстанавливаться элемент сообщения.

Однако наличие помех в реальных каналах связи может приводить к ошибочным решениям. Так, в простейшем случае колебание на входе приёмника может иметь вид.

(11.1)

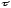Где – параметр, характеризующий затухание (ослабление) сигнала в лини связи; он может быть случайным и меняться во времени (так называемая мультипликативная помеха);– параметр, характеризующий задержку сигнала при распространении в линии, так же может иметь случайный характер;– аддитивная помеха. Каким бы образом не выбиралось множество сигналов и какой бы не был способ приёма, в реальных каналах связи всегда будут иметь место ошибочные решения. При неизменных условиях передачи всегда будет неизменной статистика ошибочных решений. Задача оптимального приёма заключается в организации такого способа передачи сообщений, который позволяет свести вероятности ошибочных решений (или эффект, связанный с ошибочными решениями) до возможного минимума. Тем самым будет обеспечена максимально возможная верность (точность) передачи сообщения.

Если при приёме сигналов учитывается статистический характер сигналов, помех и решений приёмника, то мы говорим, что приём сигналов трактуется как статистическая задача. Впервые такую постановку задачи рассмотрел В.А. Котельников.

Способность канала обеспечить заданную верность передачи в условиях действия помех называется помехоустойчивостью.

Максимум вероятности правильного приёма символа для гауссовского канала при заданном виде модуляции В.А. Котельников назвал потенциальной помехоустойчивостью, а демодулятор, обеспечивающий этот максимум – идеальным приёмником.

Из этого определения следует, что ни в одном реальном демодуляторе вероятность правильного приёма символа не может быть больше, чем в идеальном приёмнике.

11.2. Элементы теории решений

Пусть при передаче дискретных сообщений, закодированных кодом с основанием m используются реализации сигнала , 0<t<T, соответствующие кодовым символам . В течение тактового интервала 0<t<T на вход приёмного устройства поступает колебание Z(t), которое вследствие искажений и помех в канале, не совпадает в точности не с одним из сигналов . В этом случае приёмное устройство должно выбрать одну изm возможных взаимоисключающих (альтернативных) гипотез;

передавался кодовый символ , то есть сигнал.

………………………….

передавался кодовый символ , то есть сигнал.

Для двоичной системы (m=2) приёмное устройство выбирает одну из двух альтернативных гипотез о передаче символа 1 или 0.

Совокупность всех возможных реализаций Z(t) можно интерпретировать точками в пространстве Z принимаемых сигналов. Будем графически изображать реализации принимаемых сигналов и помехиn(t) длительностью Т точками на плоскости или соответствующими векторами, откладываемыми от начала координат 0. Если правило решения выбрано, то это означает, что каждой точке пространства принимаемых колебаний (концу вектора) Z=S+n приписывается одна из m гипотез, то есть определённый передаваемый кодовый символ . Пространство принимаемых сигналов окажется при этом разбитым наm непересекающихся областей , каждая из которых соответствует принятию определённой гипотезы. В такой трактовке различные приёмные устройства отличаются друг от друга способом разбииения пространства сигналов на области, то есть правилом принятия решения.

В математической теории связи это разбиение называют решающей схемой. В некоторых случаях пользуются решающей схемой со стиранием, или отказом от решения. Это значит, что m областей не охватывают всего пространства сигналов Z, и если приходящий сигнал не попадает ни в одну из этих областей, то принимается решение о стирании либо о невозможности определить передаваемый символ.

В двоичной системе пространство Z разбивают на две непересекающиеся области и. Пусть на интервале 0-Т принимается колебание

(11.2)

где – полезный сигнал в месте приёма, прошедший канал связи, аn(t) – реализация аддитивной помехи.

Если помехи отсутствуют, возможные значения изображаются точками. При наличии помехи и передаче сигнала с номеромi точка принимаемого колебания Z отклоняется от точки 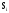. На рис. это показано для сигналов,. Обычно областьсодержит точку. В тех случаях, когда помеха не выводит точкуZ за пределы области , решение оказывается верным. В противном случае возникает ошибка. Изменяя границы между областями, можно влиять на вероятность ошибочного приёма отдельных передаваемых символов.

Например, если в разбиении, показанном на рисунке расширить область за счёт области, то уменьшится вероятность, ошибочного приёма символа, вместо предаваемого символа. Однако в этом случае возрастает вероятность ошибочного приёма передаваемого. Очевидно, всегда существует такое расположение областей, которое в определённом смысле лучше всякого другого.

Осуществить наилучшее разбиение пространства принимаемых сигналов методами теории статистических решений ( оптимизацию решающей схемы приёмного устройства) можно, если задан критерий качества.