
- •Учреждение образования «Высший государственный колледж связи»
- •Теория электросвязи
- •Раздел 1. Основы анализа сигналов.
- •1.1. Основные элементы функционального анализа сигналов. Норма и метрика.
- •1.2 Ортогональные сигналы. Ортонормированный базис. Обобщенный ряд Фурье
- •Раздел 2. Основы спектрального анализа сигналов
- •2.1 Теоремы о спектрах
- •2.3. Спектры модулированных сигналов.
- •2.3.1 Спектры амплитудно модулированных сигналов
- •2.3.2 Спектр сигналов с угловой модуляцией
- •Раздел 3. Аналитический сигнал и преобразования Гильберта
- •3.1 Аналитический сигнал. Основные понятия и определения. Спектр аналитического сигнала.
- •3.2 Преобразования Гильберта и его свойства. Применение пре образования Гильберта.
- •Раздел 4. Основы корреляционного анализа сигналов
- •4.1. Автокорреляционная функция сигналов
- •4.2. Взаимокорреляционная функция двух сигналов
- •Раздел 5. Основные элементы цифровой обработки сигналов
- •5.1. Дискретное преобразование Фурье
- •5.2. Быстрое преобразование Фурье
- •Раздел 6. Математические модели приема сигналов на фоне помех
- •6.1. Стационарные и эргодические случайные процессы.
- •6.2. Спектральное представление стационарных случайных процессов. Теорема Винера-Хинчина
- •Раздел 7. Математические модели приема сигналов на фоне помех (окончание)
- •7.1 Типовые модели случайных сигналов
- •7.2 Узкополосные случайные сигналы
- •Раздел 8. Основные сведения о шумоподобных сигналах
- •8.1 Шумоподобные сигналы и их свойства. Применение шумоподобных сигналов.
- •Раздел 9. Основы теории разделения сигналов
- •9.1 Основные положения линейной теории сигналов.
- •9.2 Структурная схема системы многоканальной передачи информации.
- •Раздел 10. Основные положения теории передачи информации
- •10.1 Информационные характеристики дискретных сообщений и сигналов
- •10.2 Взаимная информация
- •10.3. Информация в непрерывных сигналах. Дифференциальная энтропия.
- •10.4. Пропускная способность канала связи
- •10.5. Информация в непрерывных сообщениях. Эпсилон-энтропия
- •Раздел 11. Принципы оптимальной обработки сигналов на фоне помех
- •11.1. Задача оптимального приёма дискретных сообщений
- •11.2. Элементы теории решений
- •11.3. Критерии оптимизации приёма дискретных сообщений
- •11.4 Алгоритм оптимального приёма при полностью известных сигналах. (Когерентный приём)
- •Раздел 12. Принципы оптимальной обработки сигналов на фоне помех (продолжение)
- •16.5 Реализация алгоритма оптимального приема на основе корреляторов
- •12.2 Реализация алгоритма оптимального приёма на основе согласованных фильтров. Свойства согласованного фильтра
- •12.3 Потенциальная помехоустойчивость систем с различными видами манипуляции
- •Раздел 13. Принципы оптимальной обработки сигналов на фоне помех (окончание)
- •13.1 Оптимальный прием дискретных сообщений с неопределенной фазой (Некогерентный прием).
- •13.2 Помехоустойчивость систем с различными видами дискретной модуляции при некогерентном приеме
- •13.3 Прием дискретных сообщений в каналах с замираниями
- •Раздел 14. Основы цифровой обработки сигналов
- •14.1 Основные принципы цифровой фильтрации. Характеристики и свойства цифровых фильтров.
- •14.2 Алгоритм линейной цифровой фильтрации.
- •Тема 15. Основы цифровой обработки сигналов (окончание)
- •15.1 Трансверсальные цифровые фильтры.
- •15.2 Рекурсивные цф. Устойчивость цифровых фильтров
- •Раздел 16. Введение в вейвлет-преобразования сигналов
- •16.1 Понятие вейвлет-преобразования. Основные вейвлеты, применяемые в системах связи.
- •16.2 Дискретный вейвлет-анализ.
- •16.3 Непрерывное вейвлет-преобразование
- •Содержание.
Учреждение образования «Высший государственный колледж связи»
Куприянов Б.И.
Теория электросвязи
Конспект лекций
2014 г.
Предмет: «Теория электросвязи».
Целью дисциплины является изучение основных закономерностей и методов передачи информации по каналам связи. Рассматриваются математические модели сообщений, сигналов и помех, методы формирования сигналов и их преобразования в каналах связи, принципы построения систем связи, их характеристики и вопросы оптимизации.
Литература:
Баскаков С.И. Радиотехнические цепи и сигналы. – М.: Высшая школа, 2000-448с.
Зюко А.Г., Кловский Д.Д., Назаров М.В. Финк Л.М. Теория передачи сигналов. – М.: Радио и связь, 1986-304с.
Теория электрической связи. Под редакцией Кловского Д.Д. – М.: Радио и связь, 1999-432с.
Гоноровский И.С. Радиотехнические цепи и сигналы – М.: Советское радио, 1986.
Клюев Л.Л. Теория электрической связи – Мн.: Дизайн ПРО, 1998-336с.
Баскаков С.И. Радиотехнические цепи и сигналы. Руководство к решению задач – М.:: Высшая школа, 1987-206с.
Кловский Д.Д., Шилкин В.А. Теория передачи сигналов в задачах – М.: Радио и связь, 1990-280с.
Заездный А.М. Основы расчётов по статистической радиотехнике. М.: Связь, 1969.
Горяинов В.Т., Журавлёв А.Г. Тихонов В.И. Примеры и задачи по статистической радиотехнике – М.: Советское радио, 1980
Прокис Дж. Цифровая связь. Пер. с англ. / Под редакцией Д.Д. Кловского – М. Радио и связь, 2000 – 1000с.
Феер К. Беспроводная цифровая связь. Методы модуляции расширенных спектров. – М.: Радио и связь. 2000 – 520с.
Борисов В.И., Зинчук В.М. и др. Помехозащищённость систем радиосвязи / Под ред. Борисова В.И. – М.: Радио и связь, 2003-640с.
Скляр Б. Цифровая связь. Теоретические основы и практическое применение, 2-е изд.: Пер. с англ. – М.: Издательский дом «Вильямс», 2003-1104с.
Каганов В.И. Радиотехника + компьютер + Math CAD. М.: Горячая линия, 2001.
15. Радиотехнические цепи и сигналы. Примеры и задачи. Под редакцией И.С. Гоноровского – М. «Радио и связь», 1989.
16. Варакин Л.Е. Системы связи с шумоподобными сигналами. Москва, «Радио и связь», 1985.
Раздел 1. Основы анализа сигналов.
1.1. Основные элементы функционального анализа сигналов. Норма и метрика.
В основе функционального анализа сигналов лежит представление сигнала как вектора, в специальным образом сконструированном бесконечномерном пространстве.
Пусть
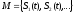 -
множество сигналов. Причина объединения
этих объектов – наличие некоторых
свойств, общих для всех элементов
множества
-
множество сигналов. Причина объединения
этих объектов – наличие некоторых
свойств, общих для всех элементов
множества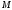 .
.
Исследование свойств сигналов, образующих такие множества, можно осуществлять, если выражать одни элементы множества через другие элементы. При этом считается, что множество сигналов наделено определённой структурой. Электрические колебания могут складываться, а также умножаться на произвольный масштабный коэффициент. Это даёт возможность в множествах сигналов ввести структуру линейного пространства.
Множество
сигналов
 образует вещественное линейное
пространство, если справедливы следующие
аксиомы:
образует вещественное линейное
пространство, если справедливы следующие
аксиомы:
Любой сигнал
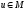 при любых
при любых принимает лишь вещественные значения.
принимает лишь вещественные значения.Для любых
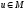 и
и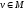 существует их сумма
существует их сумма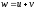 ,
причём
,
причём также содержится в
также содержится в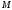 .
Операция суммирования коммутативна:
.
Операция суммирования коммутативна: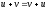 и ассоциативна
и ассоциативна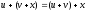 .
.Для любого сигнала
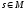 и
любого вещественного числа
и
любого вещественного числа определён сигнал
определён сигнал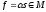 .
.Множество
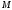 содержит особый нулевой элемент
содержит особый нулевой элемент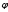 ,
такой, что
,
такой, что для всех
для всех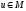 .
.
Линейное пространство, элементами которого являются функции, называется функциональным.
Если математические модели сигналов принимают комплексные значения, то, допуская в аксиоме 3 умножение на комплексное число, можем ввести понятие комплексного линейного пространства.
Как и в обычном трёхмерном пространстве в линейном пространстве сигналов можно выделить специальное подмножество, играющее роль координатных осей. В качестве таких осей используются линейно независимые векторы.
Совокупность
векторов
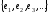 ,
принадлежащих
,
принадлежащих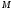 ,
является линейно независимой, если
равенство:
,
является линейно независимой, если
равенство:
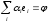
возможно лишь в
случае одновременного обращения в нуль
всех числовых коэффициентов
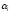 .
.
Система линейно независимых векторов образует координатный базис в линейном пространстве.
Норма и метрика. Введём новое понятие, которое по своему смыслу соответствует длине вектора. Это позволит не только определить, что один сигнал больше другого, но и указать, насколько он больше.
Длину вектора
называют его нормой. Линейное пространство
сигналов L
является нормированным, если каждому
вектору
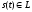 однозначно сопоставлено число
однозначно сопоставлено число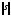 - норма этого вектора.
- норма этого вектора.
Аксиомы нормированного пространства
1. Норма неотрицательна,
т.е.
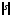
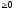 .
Норма
.
Норма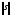 =0
тогда и только тогда, если
=0
тогда и только тогда, если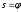
2. Для любого числа
 справедливо
равенство
справедливо
равенство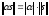 .
.
3. Если
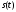 и
и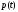 -
два вектора изL,
то выполняется неравенство:
-
два вектора изL,
то выполняется неравенство:
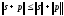
Существуют разные способы определения нормы сигналов. Чаще всего полагают, что вещественные аналоговые сигналы имеют норму:
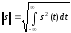 (из двух возможных значений корня
выбирается положительное). Для комплексных
сигналов норма:
(из двух возможных значений корня
выбирается положительное). Для комплексных
сигналов норма:
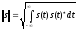 ,
,
где *-символ комплексно-сопряжённой величины.
Квадрат нормы называется энергией сигнала
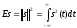
Такая энергия
выделяется в резисторе с сопротивлением
1Ом, если на его зажимах существует
напряжение
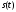 .
.
Необходимо ввести фундаментальное понятие, которое обобщало бы наше обычное представление о расстоянии между точками в пространстве.
Говорят, что
линейное пространство L
становится метрическим пространством,
если каждой паре элементов
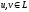 сопоставлено неотрицательное число
сопоставлено неотрицательное число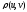 ,
называемое метрикой, или расстоянием
между этими элементами. Метрика,
независимо от способа её определения,
должна подчиняться аксиомам метрического
пространства:
,
называемое метрикой, или расстоянием
между этими элементами. Метрика,
независимо от способа её определения,
должна подчиняться аксиомам метрического
пространства:
Метрика рефлексивна
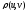 =
=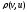
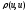 =0
при любых
=0
при любых
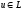 .
.Каков бы ни был элемент
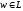 ,
всегда
,
всегда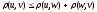 .
.
Установим взаимосвязь между нормой и метрикой. Обычно метрику определяют как норму разности двух сигналов:
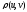 =
=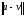
Норму в свою
очередь, можно понимать как расстояние
между выбранным элементом пространства
и нулевым элементом:
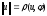 .
.
