Тема 9. Корреляционный метод анализа связей. Модели множественной регрессии

В парной корреляции исходят из постулата, что результативный признак зависит от одного факторного признака.

В действительности связь в экономических явлениях чаще является многофакторной. Уравнения, выражающие зависимость результативного признака от многих факторов, называются многофакторными (множественными) корреляционными уравнениями.

Линейное уравнение множественной регрессии в общем виде представляется формулой

,

где – значение результативного признака, соответствующее заданным факторным признакам .

, – параметры уравнения.

Параметр экономической интерпретации не имеет. Параметр называется коэффициентом условно-чистой регрессии.

Термин «коэффициент условно-чистой регрессии» означает, что каждая из величин измеряет среднее по совокупности отклонение результативного признака от его средней величины при отклонении данного фактора от своей средней величины на единицу его измерения и при условии, что все прочие факторы, входящие в уравнение регрессии, закреплены на средних значениях, не изменяются, не варьируют.

Таким образом, в отличие от коэффициента парной регрессии коэффициент условно-чистой регрессии измеряет влияние фактора, абстрагируясь от связи вариации этого фактора с вариацией остальных факторов. Если было бы возможным включить в уравнение регрессии все факторы, влияющие на вариацию результативного признака, то величины можно было бы считать мерами чистого влияния факторов. Но так как реально невозможно включить все факторы в уравнение, то коэффициенты не свободны от примеси влияния факторов, не входящих в уравнение.

Параметры уравнения , найдем методом наименьших квадратов (МНК). Для этого необходимо минимизировать сумму квадратов отклонений результативного признака от теоретического значения результативного признака , т.е. найти параметры , , при которых функция достигает минимума.

Запишем необходимые условия экстремума:

,

,

,

…

или

,

,

,

…

.

Раскроем скобки и получим стандартную форму нормальных уравнений. Параметры уравнения , найдем из решения системы этих нормальных уравнений:

Уравнение множественной регрессии в нелинейной форме не применяют в связи с тем, что их решение в математическом плане становится сверхсложной задачей.

При построении уравнения множественной регрессии принципиальное значение приобретает отбор факторов, которые будут участвовать в данной модели.

Выбранная функция должна отразить основные закономерности, но в то же время иметь по возможности простой вид.

Отбор факторов для модели может быть выполнен в следующей последовательности.

На первой стадии производится априорный анализ явления, и устанавливаются все возможные факторы.

На второй стадии осуществляется сравнительная оценка и отсев части факторов с помощью парных коэффициентов корреляции.

Если абсолютная величина парного коэффициента корреляции =0,8 и более, то факторыисчитаются коллинеарными (дублирующими друг друга) и один из них отбрасывается.

На третьей стадии выполняется многошаговый процесс вычислений с последовательным отсевом наименее значимого фактора , у которого парный коэффициент корреляцииоказался наименьшим.

Для каждой модели, включающей в себя число факторов, последовательно уменьшенное на один из них, рассчитывается совокупный коэффициент корреляции или корреляционное отношение, которые равны между собой. Модель с наибольшим совокупным коэффициентом корреляции (или корреляционным отношением) считается наиболее оптимальной.

Рассмотрим множественное уравнение регрессии с двумя признаками-факторами:

.

Параметры уравнения найдем из решения системы нормальных уравнений:

Решение данной системы имеет вид:

Совокупный коэффициент корреляции вычисляется по формуле:

,

где – это линейный коэффициент корреляции, который исчислен по указанным парам показателейи,и,и. Так, например,

,

где – среднее значение произведения признакови;

–средние значения признаков и;

–средние квадратические отклонения признаков и;

Корреляционное отношение вычисляется по формуле:

,

где – индивидуальные значения результативного признака,

–теоретические значения результативного признака, которые находятся по уравнению множественной регрессии,

–среднее значение результативного признака.

При этом совокупный коэффициент корреляции равен корреляционному отношению.

Для оценки степени соответствия модели фактическим данным служит коэффициент детерминации

.

Коэффициент детерминации показывает, какую часть фактической вариации переменной y составляет вариация регрессии.

Значимость модели множественной регрессии проверяется с помощью F-критерия Фишера. Проверяется нулевая гипотеза при конкурирующей гипотезе.

1. Наблюдаемое значение критерия находится по формуле:

,

где m – количество объясняющих переменных модели.

2. Критическую точку F-критерия Фишера определяем по соответствующей таблице

,

где - уровень значимости, обычноили(, где- доверительная вероятность);

m и n-m-1 – числа степеней свободы, а n – количество наблюдений;

3. Сравниваем наблюдаемое значение критерия и критическую точку:

Если , то принимаем нулевую гипотезу об отсутствии линейной регрессии между показателямииy.

Если , то отклоняем нулевую гипотезу о равенстве нулю коэффициента детерминации. Т.е. принимаем конкурирующую гипотезу о наличии линейной регрессии между показателямииy.

Значимость коэффициента регрессии () проверяется с помощьюt-критерия Стьюдента. Проверяется нулевая гипотеза () (о незначимости коэффициента регрессии) при конкурирующей гипотезе().

1. Наблюдаемое значение критерия находится по формуле:

(),

где () - среднеквадратическая (стандартная) ошибка параметра регрессии(), находится по формуле

(),

где - среднеквадратическая (стандартная) ошибка регрессии, рассчитывается по формуле:

2. Критическую точку t-критерия Стьюдента определяем по соответствующей таблице

,

где - уровень значимости, обычноили(, где- доверительная вероятность);

– число степеней свободы, а n – количество наблюдений;

3. Сравниваем наблюдаемое значение критерия и критическую точку:

Если , то принимаем нулевую гипотезу о незначимости коэффициента регрессии, т.е. коэффициент регрессии почти не отличается от нуля или равен нулю.

Если , то отклоняем нулевую гипотезу о незначимости коэффициента регрессии, т.е. коэффициент регрессии не равен нулю.

Значимость параметра a проверяется с помощью t-критерия Стьюдента. Проверяется нулевая гипотеза при конкурирующей гипотезе.

1. Наблюдаемое значение критерия находится по формуле:

,

где - среднеквадратическая (стандартная) ошибка параметра регрессииa.

;

2. Критическую точку t-критерия Стьюдента определяем по соответствующей таблице

;

3. Сравниваем наблюдаемое значение критерия и критическую точку:

Если , то принимаем нулевую гипотезу о незначимости параметраa, т.е. параметра a почти не отличается от нуля или равен нулю.

Если , то отклоняем нулевую гипотезу о незначимости параметраa, т.е. параметра a не равен нулю.

Доверительные интервалы параметров регрессии при уровне значимости определяются по формулам:

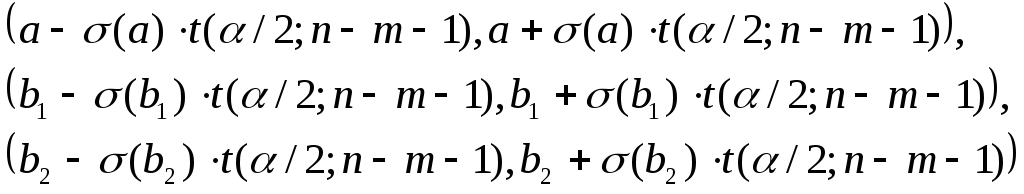
где ,,- среднеквадратические ошибки параметров регрессииa, и , соответственно,

- табличное значение критерия Стьюдента при заданном уровне значимости и числе степеней свободы.

Точечный прогноз находится по построенной модели множественной линейной регрессии.

Пример. Имеются данные об объеме сбережений домохозяйства, располагаемого им дохода и процентной ставки за 11 лет (см. табл. 9.1).

Таблица 9.1

Год	Располагаемый доход домохозяйства, тыс. руб.	Процентная ставка, %	Объем сбережений домохозяйства, тыс. руб.
1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 1990	100 110 140 150 160 160 180 200 230 250 260	2 2 3 2 3 4 4 3 4 5 5	20 25 34 30 36 37 40 46 58 69 80

Необходимо:

1) построить модель множественной линейной регрессии зависимости объема сбережений домохозяйства от располагаемого им дохода и процентной ставки;

2) оценить тесноту связи между указанными признаками с помощью совокупного коэффициента корреляции;

3) определить значимость построенной модели с помощью коэффициента детерминации;

4) при уровне значимости проверить значимость

а) модели множественной линейной регрессии,

б) параметров регрессии

и сделать соответствующие выводы;

5) построить 95%-ные доверительные интервалы для найденных параметров регрессии.

6) спрогнозировать средний объем сбережений в 1991 году, если предполагаемый доход составит 170 тыс. руб., а процентная ставка будет равна 5,5%.

Решение.

1) Так как объем сбережений домохозяйства зависит от располагаемого им дохода и процентной ставки, то в качестве факторных признаков (и) будут выступатьдоход и процентная ставка, а в качестве результативного (y) – объем сбережений.

Для нахождения параметров множественной регрессии рассчитаем необходимые суммы и средние величины (см. табл. 9.2 и 9.3).

Таблица 9.2

Год			y
1980	100	2	20	5831,405	1,860
1981	110	2	25	4404,132	1,860
1982	140	3	30	1322,314	0,132
1983	150	2	30	695,041	1,860
1984	160	3	35	267,769	0,132
1985	160	4	38	267,769	0,405
1986	180	4	40	13,223	0,405
1987	200	3	38	558,678	0,132
1988	230	4	44	2876,860	0,405
1989	250	5	50	5422,314	2,678
1990	260	5	55	6995,041	2,678
Сумма:	1940	37	405	28654,545	12,545
Среднее:	176,364	3,364	36,818

Таблица 9.3

Год
1980	104,132	1284,298	22,934	282,851
1981	90,496	784,298	16,116	139,669
1982	13,223	247,934	2,479	46,488
1983	35,950	179,752	9,298	46,488
1984	5,950	29,752	0,661	3,306
1985	-10,413	-19,339	0,752	1,397
1986	2,314	11,570	2,025	10,124
1987	-8,595	27,934	-0,430	1,397
1988	34,132	385,207	4,570	51,579
1989	120,496	970,661	21,570	173,760
1990	136,860	1520,661	29,752	330,579
Сумма:	524,545	5422,727	109,727	1087,636

Тогда

Таким образом, модель множественной линейной регрессии имеет вид

.

2) Оценим тесноту связи между указанными признаками с помощью совокупного коэффициента корреляции. Средние значения признаков ,иy найдены в таблице 9.2. Рассчитаем дисперсии и среднеквадратические отклонения этих признаков (необходимые суммы найдены в таблицах 9.2 и 9.3):

; (тыс. руб.);

; (%);

; (тыс. руб.).

Рассчитаем в таблице 9.4 суммы и средние величины, необходимые для нахождения парных линейных коэффициентов корреляции.

Таблица 9.4

Год			y
1980	100	2	20	200	2000	40
1981	110	2	25	220	2750	50
1982	140	3	30	420	4200	90
1983	150	2	30	300	4500	60
1984	160	3	35	480	5600	105
1985	160	4	38	640	6080	152
1986	180	4	40	720	7200	160
1987	200	3	38	600	7600	114
1988	230	4	44	920	10120	176
1989	250	5	50	1250	12500	250
1990	260	5	55	1300	14300	275
Сумма:	1940	37	405	7050	76850	1472
Среднее:	176,364	3,364	36,818	640,909	6986,364	133,818

Найдем парные линейные коэффициенты корреляции:

,

,

.

Итак, совокупного коэффициента корреляции

,

что свидетельствует о весьма высокой связи между этими признаками, т.е. между объемом сбережений домохозяйства, располагаемого им дохода и процентной ставкой.

3) Коэффициент детерминации , следовательно, модель объясняет зависимость между переменными на 97,8 %.

4а) При уровне значимости проверим гипотезу о значимостимодели множественной линейной регрессии.

,

.

1. Наблюдаемое значение критерия:

,

2. Критическая точка ,

3. Т.к. (175,4735>4,46), то отклоняем нулевую гипотезу о равенстве нулю коэффициента детерминации. Т.е. принимаем конкурирующую гипотезу о наличии линейной регрессии между показателямииy (совокупное влияние переменных ина переменнуюy существенно).

4б) При уровне значимости проверим гипотезы о значимости параметров регрессии.

Рассчитаем стандартную ошибку регрессии, для этого в таблице 9.5 найдем теоретические значения и .

Таблица 9.5

Год			y
1980	100	2	20	22,489	6,1927
1981	110	2	25	23,730	1,6119
1982	140	3	30	31,010	1,0199
1983	150	2	30	28,698	1,6953
1984	160	3	35	33,494	2,2690
1985	160	4	38	37,048	0,9072
1986	180	4	40	39,531	0,2197
1987	200	3	38	38,461	0,2127
1988	230	4	44	45,741	3,0302
1989	250	5	50	51,778	3,1626
1990	260	5	55	53,020	3,9193
Сумма:	1940	37	405	405	24,2406

Тогда .

Для коэффициента регрессии :

,

.

1. Наблюдаемое значение критерия:

,

где

;

2. Критическая точка ;

3. Т.к. (5,8495>2,31), то отклоняем нулевую гипотезу о незначимости коэффициента регрессии.

Для коэффициента регрессии :

,

.

1. Наблюдаемое значение критерия:

,

где ;

2. Критическая точка ;

3. Т.к. (3,5025>2,31), то отклоняем нулевую гипотезу о незначимости коэффициента регрессии.

Для параметра регрессии a:

,

.

1. Наблюдаемое значение критерия:

,

где

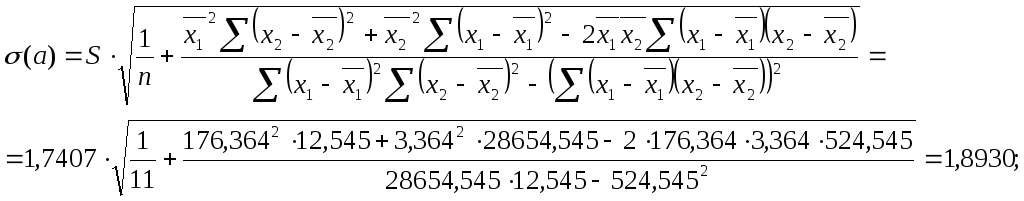
2. Критическая точка ;

3. Т.к. (1,5647<2,31), то принимаем нулевую гипотезу о незначимости параметраa, т.е. параметра a почти не отличается от нуля или равен нулю, и он может не использоваться в модели. Однако наличие свободного члена в линейном уравнении может лишь уточнить вид зависимости. Поэтому, если нет серьезных причин для удаления свободного члена из уравнения регрессии, то лучше его использовать в модели.

5) Построим 95%-ные доверительные интервалы для найденных параметров регрессии в соответствии с выше приведенными формулами.

Для параметра регрессии a:

или (-1,4031;7,3270),

для коэффициента регрессии :

или (0,0753;0,1731),

для коэффициента регрессии :

или (1,2142;5,8935).

6) Прогноз среднего объема сбережений в 1991 году найдем по построенной модели множественной линейной регрессии.

(тыс. руб.).