10.3. Ограниченная взаимная растворимость трех жидкостей

Жидкие трехкомпонентные системы могут состоять как из жидкостей, дающих растворы любого состава, так и взаимно ограниченно растворимых. В последнем случае на диаграмме появляется область расслаивания. Фигуративной точке системы, лежащей внутри этой области, соответствуют две фигуративные точки двух растворов, на которые распадается система. Взаимная растворимость трех жидкостей зависит от температуры, и в ряде случаев при соответствующей критической температуре наступает неограниченная взаимная растворимость всех трех компонентов.

Рис. 10.8. Объемная диаграмма состояния трехкомпонентной жидкой системы с областью расслоения и ее изотермическое сечение

На рис. 10.8 показана диаграмма состояния простейшей системы, в которой компоненты A и C, а также B и C неограниченно взаимно растворимы, а компоненты A и B ограниченно растворимы друг в друге. Составы двух фаз, на которые распадается система, отвечающая, например, фигуративной точкер, могут быть определены только опытным путем. Это связано с тем, что в данном случае графически невозможно найти направление нод, так как вся плоскость треугольника относится к одной и той же температуре.

По эмпирическому правилу Тарасенковапродожения всех нод на диаграмме пересекаются в одной точке. На приведенной диаграмме одной из нод является отрезокab, лежащий на стороне треугольника. Поэтому точка пересеченияовсех нод должна лежать на продолжении этой стороны. Определив опытным путем составы хотя бы одной пары сопряженных растворов, например,mиn, можно найти точкуои по ней построить все другие ноды для области расслаивания. Касательная, проведенная из точкиок кривойamdnb, дает точкуd, соответствующую составу, при котором система становится гомогенной при данной температуре. Однако, правило Тарасенкова не является строгим и выполняется не для всех систем.

Добавление третьего компонента к бинарной системе может увеличивать или уменьшать взаимную растворимость. Если вводимое вещество растворимо в обоих компонентах, то их взаимная растворимость увеличивается. Например, при добавлении определенного количества спирта к двухфазной системе эфир – вода наступает неограниченная растворимость. Добавка же вещества, не растворимого в одном из компонентов, понижает взаимную растворимость.

Это свойство бинарных систем используется в аналитических целях. Например, критическая температура растворимости абсолютного спирта и парафинового масла повышается от 92 до 97 С при добавлении к спирту 1% воды. Это позволяет определять небольшие примеси воды к спирту. Подобный метод применяется при анализе жиров, динамита и др.

10.4. Распределение вещества между двумя несмешивающимися растворителями

Если две жидкости не растворяются друг в друге или ограниченно взаимно растворимы, то их смесь образует двухфазную систему, каждая фаза которой является индивидуальным компонентом или раствором одного компонента в другом. При добавлении к этой системе вещества, которое растворимо в обеих фазах, оно распределится между двумя фазами, образуя растворы различных концентраций. При достижении равновесия химические потенциалы добавленного вещества в первой фазе и во второй фазебудут равны:

+RTln=+RTln, (10.1)

где і– активности распределенного вещества в первой и второй фазах,^о– соответствующие стандартные химические потенциалы.

Из уравнения (10.1) следует, что

ln==а(Т) =const(Т),(10.2)

т.е. логарифм отношения активностей распределенного вещества при заданной температуре есть постоянная величина. Следовательно, и само отношение активностей растворенного вещества в двух фазах является постоянным:

=K_r=f (Т). (10.3)

Величина K_rназываетсяконстантой распределения, а уравнение (10.3) является математическим выражениемзакона распределения Нернста: распределение каждого из растворенных веществ между двумя фазами определяется индивидуальным коэффициентом распределения, величина которого не зависит от присутствия других веществ.

В случае идеальных или предельно разбавленных растворов вместо активностей в уравнении Нерста можно использовать мольные доли или другие способы выражения состава растворов, например, молярные концентрации:

=K_rабо =K_r. (10.4)

Закон распределения Нерста строго выполняется лишь в том случае, когда добавляемое вещество не изменяет взаимную растворимость жидкостей и находится в обеих фазах в одинаковой форме. Если, например, вещество в одной фазе находится в молекулярной форме, а в другой фазе диссоциирует или ассоциирует, то следует учесть эти дополнительные равновесия.

Из закона распределения следует, что вещество, растворенное в одном растворителе, можно извлечь из раствора с помощью другого растворителя, не смешивающегося с первым. Такой процесс извлечения растворенного вещества называется экстракцией. Процессы экстракции широко используются для концентрирования вещества, разделения веществ и их очистки, в аналитических определениях.

Эффективность экстракции тем выше, чем больше коэффициент распределения в пользу второго растворителя, а также при многократной экстракции небольшими порциями растворителя вместо однократной экстракции большим объемом. Это следует из закона распределения (10.4). Рассчитаем количество вещества, остающегося в исходном растворе после nэкстрагирований. Пусть исходный раствор объемомV_о содержитaграммов (или молей) вещества, т. е. его концентрация равнаa/V_о. После добавки первой порции экстрагента объемаV_ев исходном растворе останетсяg₁г вещества, а в экстрагент перейдет (a–g₁) г. Таким образом, после первой экстракции концентрация вещества в первой фазе будет равнас^(I)=х₁/V_о, а во второй –с^(II)= (а–g₁)/V_е, и по закону распределения

абоg₁=а. (10.5)

После второй экстракции таким же объемом экстрагента в растворе останется g₂ растворенного вещества, а в экстрагент перейдет (g₁–g₂) вещества. Тогда

,g₂=g₁ = a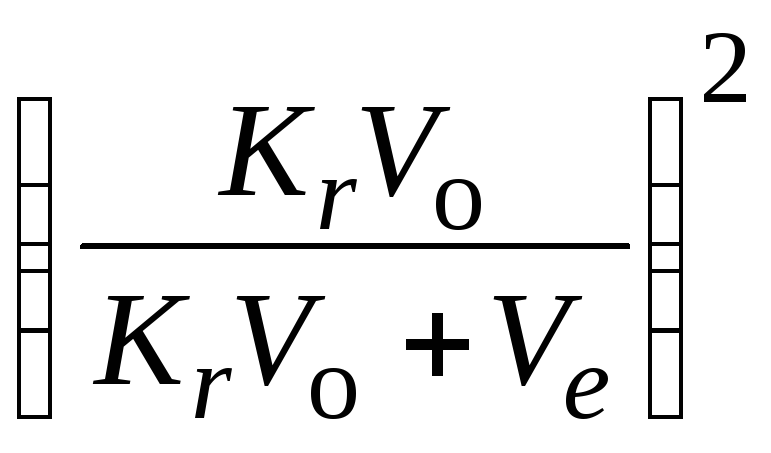(10.6)

или после nэкстрагирований

g_n=а. (10.7)

Если, например, исходный раствор содержит 100 г вещества в одном литре и экстрагирование проводить 1 л экстрагента, то при K_r= 0,2 в растворе останетсяg₁= 16,6 г вещества. При двойном экстрагировании порциями по 0,5 л в растворе останетсяg₂= 8,16 г, а при четырехкратном экстрагировании порциями по 0,25 л останется 3,90 г. Таким образом, степень извлечения вещества составляет 83,4; 91,84 и 96,10% соответственно.