6.2 Определение параметров выборочного уравнения прямой линии

Предположим, что проведено п независимых опытов, в результате которых получены п пар чисел:

, … … ,

где у₁, у₂, … у_n – математические ожидания ординат функции.

Можно рассчитать средние арифметические наблюдаемых значений переменных Х и Y по уравнениям:

; (6.2)

. (6.3)

и их стандартные отклонения по уравнениям:

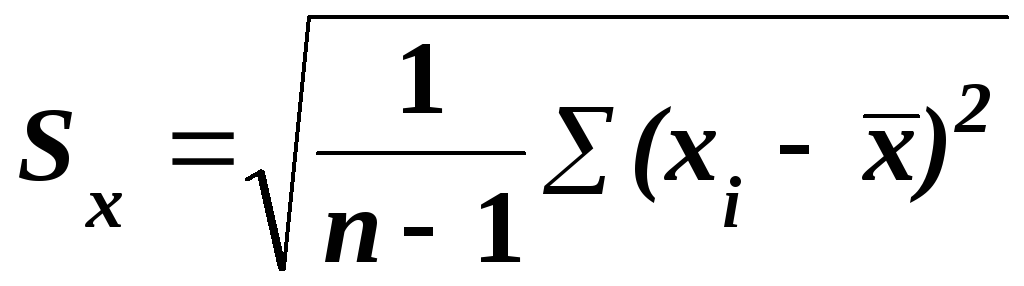; (6.4)

. (6.5)

Здесь i – порядковый номер аргумента x_i и соответствующего ему математического ожидания ординаты функции у_i;

 – знак, обозначающий сумму всех n значений x_i и y_i.

Поскольку наблюдаемые пары чисел можно рассматривать как случайную выборку из генеральной совокупности всех возможных значений случайных величин Х и Y, то величины и уравнения, найденные по этим данным, называют выборочными.

Будем искать выборочное уравнение прямой линии регрессии Y на Х:

(6.6)

Угловой коэффициент прямой линии регрессии Y на X – b₁ принято называть выборочным коэффициентом регрессии Y на Х. Часто применяют обозначение коэффициента регрессии .

Способ определения параметров уравнения регрессии – метод наименьших квадратов. При этом методе принимается, что сумма квадратов отклонений значений у_i от вычисленных по уравнению регрессии значений для соответствующих значенийх_i, т.е. от искомой линии регрессии должна быть минимальной:

(6.7)

Значения параметров уравнения регрессии могут быть найдены по формулам:

; (6.8)

. (6.9)

Необходимо проверить гипотезу о статистической значимости коэффициентов регрессии, иными словами, проверить, существенно ли их величина отличается от 0.

Оценку статистической значимости коэффициентов регрессии устанавливают на основе t-критерия Стьюдента. Расчётное значение t-критерия определяют для каждого коэффициента регрессии из соотношения:

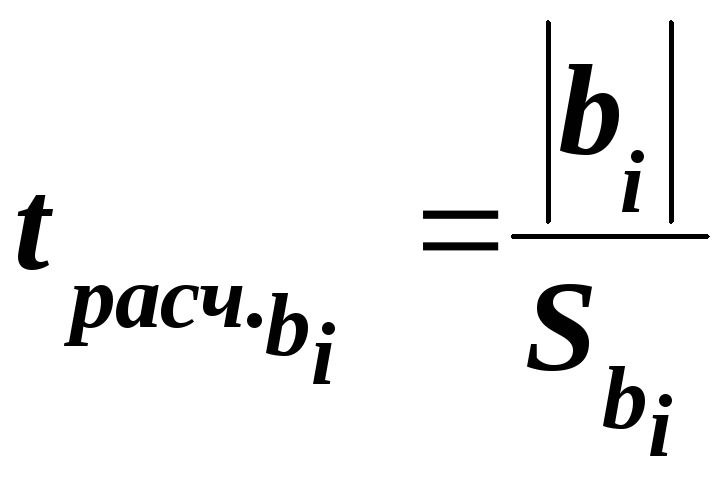, (6.10)

где – стандартная ошибка коэффициента b_i, величина которой в общем случае может быть определена по формуле:

_(6.11)

Если выполняется соотношение:

, (6.12)

то коэффициент регрессии b_i признаётся статистически значимым при выбранном уровне значимости α. Если же это соотношение не выполняется, то коэффициент b₁ признаётся незначимым. Следовательно, можно соответствующее слагаемое исключить из уравнения регрессии.

Если при каждом из n значений аргумента было выполнено одинаковое количество m параллельных измерений ординат функцииY, то с помощью критерия Кохрена проверяют воспроизводимость эксперимента. Расчётное значение критерия Кохрена определяют по формуле:

, i = 1 … n. (6.13)

где – максимальная из п дисперсий ординат при всех значениях , а  дисперсия ординат , соответствующих значениям аргументов , величину которой вычисляют по формуле:

; j = 1 … m. (6.14)

Если выполняется соотношение:

G_расч. ≤ G_{табл. α, n(m – 1)}, (6.15)

то эксперимент признают воспроизводимым. При этом ошибку опытов оценивают как среднеквадратичную ошибку при определении средних значений из измерений, выполненных при значениях , по формуле:

. (6.16)