Совмещенная частотная характеристика (афчх)

Обыкновенные АЧХ и ФЧХ можно объединить в одну характеристику, используя А(ω) и φ(ω) в качестве полярных координат.

На рис. 5 показано построение совмещенной амплитудно–фазовой характеристики (АФХ). При этом на луче, выходящем из начала координат под углом φ(ω_i), откладывается A(ω_i). На такой характеристике частота в явном виде отсутствует. Однако каждой точке на кривой соответствует определенная частота.

Амплитудно-фазовой характеристикой (АФХ) называют годограф, который описывает конец вектора А(ω) при изменении частоты ω от 0 до ∞. Таким образом

АФХ = АЧХ + ФЧХ .

Рис. 5. Построение АФХ

Частотная передаточная функция

Если в передаточную функцию вместо оператора Лапласа подставить мнимую переменную Фурье , получим частотную передаточную функцию , которую называют просто частотной функцией. Ее можно представить в виде действительной 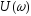и мнимойчастей (компонент)

или в комплексной форме

,

где – модуль частотной функции, а – ее фаза.

Покажем связь между компонентами частотной функции и амплитудно–фазовой характеристикой (АФХ). Для этого на комплексной плоскости (рис. 6) отложим действительную и мнимую части. Если полученную точку А соединить с началом координат, получим вектор , длина (модуль) которого равен, а аргумент (угол, образованный этим вектором с действительной положительной полуосью).

Таким образом,.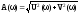

Рис. 6. Построение АФХ по компонентам частотной функции

Частотные функции соединений звеньев

Если известны частотные характеристики отдельных звеньев, то можно построить и частотные характеристики их соединений.

При параллельном соединении частотная функция равна сумме вещественной и мнимой частей частотных функций звеньев +,

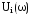при этом векторы Аi (ω) можно графически суммировать.

При последовательном соединении следует перемножить модули и сложить фазы частотных функций

;

.

При охвате звена обратной связью результирующую частотную характеристику получают с помощью специальных номограмм.

Логарифмические частотные характеристики

При исследовании систем управления частотные характеристики удобно строить в логарифмических координатах по таким причинам: 1) в большинстве случаев АЧХ звеньев в логарифмических координатах можно представить отрезками прямых линий; 2) АЧХ цепочки звеньев графически суммируются.

АЧХ в логарифмических координатах строится в виде зависимости lg A от lg ω, называемой логарифмической амплитудно–частотной характеристикой (ЛАЧХ), а фазовая – в виде зависимости φ от lg ω, наз. логарифмической фазочастотной характеристикой (ЛФЧХ).

При этом за единицу масштаба частоты принимается декада – частотный интервал, соответствующий изменению частоты в 10 раз.

При построении ЛАЧХ по оси ординат откладывают выходную величину L(ω), измеряемую в децибелах (дБ). Бел – единица десятичного логарифма коэффициента усиления мощности сигнала. Один бел соответствует усилению мощности в 10 раз, 2 бела – в 100 раз, 3 бела – в 1000 раз и т.д.

Поскольку мощность сигнала пропорциональна А², то ее усиление в белах в логарифмических координатах равно lg A² = 2 lg A (в децибелах – 20 lg A.).

Таким образом – L(ω) = 20 lg A(ω).

Соотношение A и L приведено в следующей таблице

А (раз)	0,01	0,1	0,5	1,0	1,12	1,41	2,0	3,6	10	100
L (дБ)	–40	–20	–6	0	1	3	6	10	20	40

При построении ЛФЧХ фаза откладывается по оси ординат в радианах или угловых градусах в обычном масштабе, т.к. фазовый сдвиг цепочки звеньев равен сумме фазовых сдвигов на отдельных ее звеньях. При совместном анализе ЛАЧХ и ЛФЧХ на оси абсцисс применяют логарифмический масштаб частоты в декадах или в октавах (одна октава соответствует изменению частоты в два раза).

Отметим, что при использовании логарифмического масштаба точка, соответствующая ω = 0, находится в минус  ∞, а нулю на оси абсцисс соответствует точка ω = 1 рад/с.

УСТОЙЧИВОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Одним из основных условий работоспособности САУ является ее устойчивость, т.е. способность системы возвращаться в исходное состояние после снятия или прекращения изменения воздействия, выведшего ее из этого состояния. Понятие устойчивости неразрывно связано с понятием равновесия.

Равновесным состоянием тела (или системы) называется такое состояние, в котором сумма всех внеш­них воздействий равна нулю. Равновесное состояние может быть устойчивым, неус­тойчивым и нейтральным.

Классической иллюстрацией этого положения (рис.9.1) яв­ляется поведение шарика, помещенного: на дно лунки (а), на вершину холма (б) и на горизонтальную плоскость (в). В каждом из этих случаев сумма внешних сил, дей­ствующих на шарик, равна нулю и, следовательно, ша­рик находится в состоянии равновесия.

Рис. 9.1. Механическая интерпретация понятия устойчивости

Однако, если в первом случае после небольшого отклонения шарик через некоторое время вновь возвращается в исходное положение равновесия, то во втором он будет продолжать отклоняться от него, а в третьем – просто перейдет в новое положение равновесия, зависящее от величины отклонения.

Кроме того, такая система может быть устойчива при воздействиях, не выходящих за определенные пределы – «в малом», и неустойчива при больших воздействиях – «в целом» (см. рис.9.1, г).

Рассмотрим с этой точки зрения системы автоматиче­ского управления.

Каждая САУ характеризуется неким равновесным состоянием, которое нарушается при внешних воздейст­виях. Это могут быть сигналы управления, помехи и т.п. Под устойчивостью САУ подразумевается свойство системы возвращаться к первоначальному состоянию после прекращения воздействия, выведшего систему из этого состояния.

Обозначим у(t₀) – значение выходной величины в исходном равновесном состоянии системы (в момент времени t = t₀), y(t) – текущее значение выходной величины после нанесения возмущения f(t).

САУ будет являться устойчивой, если при t величина y(t) стремится к своему начальному значению y(t₀) в случае f(t) = сonst или после снятия воздействия f(t)=0.

Если при этом амплитуда отклонения выходной величины объекта управления не превышает допустимых по технологии значений, а наличие ее колебаний не ухудшает работу агрегата – такую систему можно эксплуатировать.

Неустойчивая система не возвращается к состоянию равновесия по окончании или стабилизации воздействия, а непрерывно удаляется от него или совершает недопустимо большие колебания.

Заметим, что нейтральные САУ, в которых по окончании воздействия устанавливается новое состояние равновесия, отличное от первоначального и зависящее от произведенного воздействия, являются неустойчивыми.

Реальные системы обычно работают в условиях непрерывно изменяющихся воздействий, при этом установившиеся режимы вообще отсутствуют. В таких случаях применяют обобщенное определение: Система динамически устойчива, если ее выходная величина остается в пределах допустимых отклонений в условиях действия ограниченных возмущений.

В связи с этим можно сказать, что системы автоматического управления устойчивы, если происходящие в них переходные процессы сходятся. Выясним, какими особенностями математического описания систем определяется эта сходимость.

Переходные процессы в системе описываются общим решением однородного уравнения An(p) = 0 или

.

Это решение представляет собой сумму экспонент .

Здесь – постоянные интегрирования, а – корни характеристического уравнения .

В общем случае корни 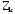являются комплексными, образуя пары сопряженных корней –Z _k, k+1 =  _k    j  _k . Каждая пара корней дает свою составляющую общего решения в виде

.

Эти функции представляют собой синусоиды с амплитудами, изменяющимися во времени по экспоненте. При этом, если  _k < 0 , то k-я составляющая будет затухать. Наоборот, при  _k > 0 получатся расходящиеся колебания. Если  _k = 0 (мнимые корни), имеем незатухающие стационарные колебания.

Таким образом, необходимым и достаточным условием сходимости переходных процессов и, следовательно, устойчивости системы является отрицательность действительной части  комплексных корней ее характеристического уравнения.

Следовательно, условием устойчивости линейной системы является расположение всех корней , которые называют полюсами передаточной функции системы, в левой комплексной полуплоскости. Наличие корня на мнимой оси означает, что система находится на границе устойчивости.

Вычисление корней просто лишь для характеристического уравнения 1-й и 2-й степени. Существуют общие выражения для корней уравнений 3-й и 4-й степени, но эти выражения громоздки и их невозможно применить для аналитического исследования влияния параметров системы на ее устойчивость.

Поэтому используются правила, которые позволяют определять устойчивость системы без вычисления корней. Эти правила называют критериями устойчивости. Все они математически эквивалентны, так как решают вопрос о знаке действительной части корней характеристического уравнения. Критерии делят на алгебраические и частотные.

Наиболее известен алгебраический критерий устойчивости Рауса – Гурвица, который позволяет судить об устойчивости системы по коэффициентам многочлена

An(p) = a_n pⁿ + a_n-1 p^n-1 + ... + a₁ p + a_{0 .}

Во-первых, необходимым (но, недостаточным!) условием устойчивости является положительность всех коэффициентов a_n, ..., a₀. Если хотя бы один из коэффициентов меньше нуля, то система неустойчива и дальнейшее исследование не имеет смысла. Если a_i>0, то согласно алгебраическому критерию устойчивости Гурвица система устойчива, если все ее определители _i больше нуля.

Исследуют систему на устойчивость по критерию Гурвица следующим образом. Для коэффициентов многочлена составляют квадратную матрицу n х n, по главной диагонали которой записывают все коэффициенты от a_n-1 до a₀ и далее заполняют ее, как показано ниже. В случае отсутствия данного коэффициента и если его номер больше n или меньше нуля, на его место проставляют нуль.

На главной диагонали определителя оказываются последовательно все коэффициенты, кроме a_n.

Определители Гурвица составляют так

₁ = a_{n-1 > 0;} и т.д.

Последний определитель включает всю матрицу. Но каждый последующий определитель может быть вычислен через предыдущий. Так как в устойчивой системе _n-1 > 0, то положительность последнего определителя обеспечивается, если a_{0 > 0.}

Рассмотрим критерий Гурвица для систем первых трех порядков.

1) Для n = 1 – An(p) = a₁p + a_{0 ,} и условие устойчивости инерционного звена сводится к неравенствам

a₁ > 0; a₀ > 0.

2) Для n = 2 – An(p) = a₂p² + a₁p + a₀ ,

Поэтому для звена 2-го порядка условие устойчивости имеет вид –

a₂ > 0; a₁ > 0; a₀ > 0.

Например, звено с передаточной функцией W(p) = k/(T₂²p²+T₁p+1) устойчиво, если перед всеми членами в знаменателе стоит знак плюс.

3) Если n = 3, то An (p) = a₃p³ + a₂p² + a₁p + a₀ и определитель Гурвица –

.

В этом случае условия устойчивости имеют вид –

a₃ > 0; a₂ > 0;

₃ = a₀ ₂ > 0.

Если  ₂ > 0, то a₀ > 0. Таким образом, условие устойчивости сводится к положительности всех коэффициентов и предпоследнего минора  ₂.

В общем случае системы любого порядка необходимым условием устойчивости является требование положительности всех коэффициентов a_i. Анализ устойчивости надо начинать с проверки этого простого условия. Если оно не выполняется, то отпадает необходимость в составлении и проверке остальных неравенств.

Для характеристических уравнений невысоких порядков (до 3-го) применение алгебраических критериев достаточно просто. Если же уравнение имеет высокий порядок (n > 4) или система включает звено запаздывания, то применить алгебраические критерии для исследования устойчивости систем затруднительно.

В подобных случаях используют частотные критерии (например, критерий Михайлова).

Области устойчивости САУ в фазовом пространстве параметров

При анализе САУ строят область устойчивости (О.У.) системы в пространстве варьируемых параметров. В случае если параметров два – О.У. можно изобразить фигурой на плоскости с координатами, например, коэффициента передачи К и постоянной времени Т. При этом вдоль границы наносится штриховка, обращенная внутрь О.У.

При большем числе варьируемых параметров граница О.У. представляет гиперповерхность в N-мерном пространстве. При практических расчетах такие О.У. изображаются в виде линий в плоскости двух выбранных для анализа параметров при фиксированных значениях остальных характеристик САУ. Эти линии геометрически являются плоскими сечениями гиперповерхности (см. приведенный ниже рисунок).

Все пространство вне О.У. наз. областью неустойчивости.

Если САУ в пространстве всех своих параметров не имеет О.У., она наз. структурно неустойчивой. Для достижения устойчивости необходимо изменить (скорректировать) структуру такой системы.

Коррекция динамических свойств САУ применяется для обеспечения устойчивости неустойчивых систем, а также расширения О.У. и повышения качества переходных процессов устойчивых систем.

Осуществляется коррекция добавлением в систему корректирующих звеньев со специально подобранной передаточной функцией. По способу включения в систему корректирующие звенья делятся на последовательные и параллельные.

Действие корр. звеньев:

1) ввод в контур САУ воздействий по производным и интегралам входной величины;

2) ввод корректирующих обратных связей для отдельных подсистем;

3) ввод корректирующих воздействий в функции внешних воздействий и их производных.

Причем, в первом и третьем случае применяют последовательные, а во втором параллельные корр. звенья.

Набольшее распространение в практике автоматизации получили последовательные корректирующие звенья.