ASD_Lecture02

Є тисячі способів, як убити час але ніхто не знає, як його воскресити.

Альберт Айнштайн

Теорія алгоритмів

Лекція 2: Аналіз ефективності алгоритмів

др.інж., доцент Андрій Керницький kernitsky@polynet.lviv.ua

к.т.н. , доцент Павло Денисюк

Теорія алгоритмів

Історія питання

Ще донедавна пошук кращих алгоритмів не викликав інтересу ні для задач малої розмірності, ні для задач великої розмірності.

Відповідь:

У випадку малої розмірності задачі кращі алгоритми ненабагато ефективніші за алгоритм повного перебору, а відсутність потужних обчислювачів призводило до того, що і у випадку задач великої розмірності ці алгоритми, так само як і природні алгоритми, не приводили до розв’язку через великий об’єм обчислень.

Лекція 2

Теорія алгоритмів

Що слід розуміти під поняттям ефективного алгоритму?

Одну і ту саму задачу можуть вирішувати багато алгоритмів. Аналіз алгоритмів дає нам інструмент для вибору алгоритму.

Ефективність роботи кожного з алгоритмів описується різними характеристиками.

•Використання процесора (час)

•Використання пам’яті

•Використання дискового простору

•Використання мережі

Лекція 2

Теорія алгоритмів

Складність алгоритму

Складність по пам’яті

- Кількість і розмір структур даних які використовуються в алгоритмі

Часова складність

- Кількість елементарних операцій, які виконуються під час виконання алгоритму

Лекція 2

Теорія алгоритмів

Продуктивність vs. Складність

1.Продуктивність/ швидкодія (performance):

скільки використовується процесорного часу, пам’яті, дискового простору під час виконання програми. Це залежить від моделі комп’ютера, компілятора, коду програми тощо.

2. Cкладність (сomplexity): як добре масштабуються вимоги до ресурсів під час виконання програми або алгоритму. Що станеться якщо розмір задачі зросте?

Лекція 2

Теорія алгоритмів

Що це значить на практиці?

На практиці, часова складність визначає придатність алгоритмів

Тому що:

це міф, коли говорять, що комп'ютери настільки

швидкодіючі, що час не становить проблеми

(розподіл простих множників великих чисел - 300 цифр - вимагає мільйони років)

•необхідне вирішення все більших проблем:

-Комп'ютерні системи підтримки прийняття рішень

-Комп'ютерне моделювання та прогнозування

•Комп'ютерні системи реального часу

-Автоматичний контроль складних систем

Лекція 2

Теорія алгоритмів

Приклад

Алгоритм підрахунку кількості входжень різних символів у файл

для всіх 256 символів виконувати

обнулити лічильник

кінець для поки у файлі ще залишилися символи виконувати

ввести черговий символ

збільшити лічильник входжень прочитаного символа на одиницю

кінець поки

Теорія алгоритмів

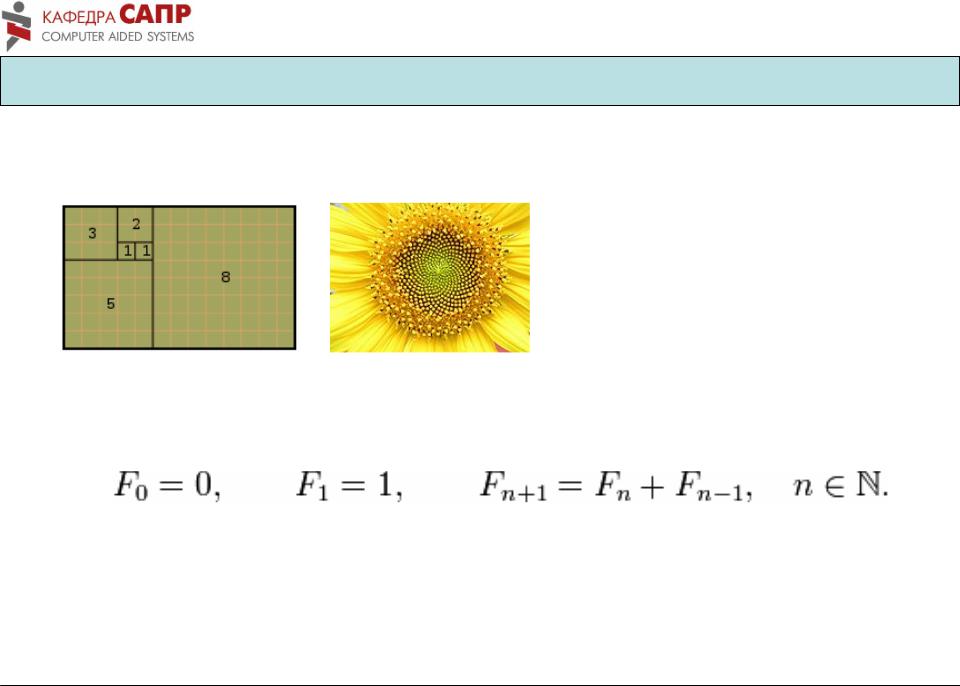
Послідовність Фібоначчі

•0, 1, 1, 2, 3, 5, 8, 13, 21, 34, . . .

Суцвіття соняшника з 34 спіралями в один бік і 55 в інший

•Формально, послідовність чисел Фібоначчі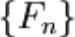

задається лінійним рекурентним співвідношенням

•швидкість зростання є експотенційною :

F30 > 1000000, десятковий запис числа F100

складається з 21-ї цифри

•Fn ≈ 20.694n

Лекція 2

Теорія алгоритмів

Експотенційний алгоритм

Алгоритм Fib1(n)

•якщо n = 0: повернути 0

•якщо n = 1: повернути 1

•повернути Fib1(n - 1)+Fib1(n - 2)

Лекція 2

Теорія алгоритмів

Аналіз алгоритмів

Для кожного алгоритму ми повинні відповісти на наступні запитання:

1.Чи алгоритм є коректним?

2.Який час його роботи (як функція від довжини входу)?

3.Чи існує швидший алгоритм?

Лекція 2