
ASD_Lecture02
.pdf
Теорія алгоритмів
Час роботи в гіршому і середньому випадку
Як ми встановили, час роботи у кращому і гіршому випадку можуть сильно відрізнятися. Ми будемо вивчати час роботи у гіршому випадку, яке дорівнює максимальному часу роботи на всіх входах даного розміру. Причини:
•Знаючи час роботи у гіршому випадку, можна гарантувати, що алгоритм завершиться за деякий час на будь-якому вході даного розміру.
•На практиці "погані" входи можуть траплятися часто.
•Час роботи в середньому може бути близьким до часу роботи у гіршому випадку.
Лекція 2

Теорія алгоритмів
Поліноміальні алгоритми vs. Експотенційні алгоритми
Між цими класами алгоритмів є істотна різниця:
при великих розмірностях задач (які, звичайно, найцікавіші на практиці), поліноміальні алгоритми можуть бути виконані на сучасних комп'ютерах, тоді як експоненціальні алгоритми для практичних размірностей задач, як правило, не можуть виконатися повністю.
Звичайно розв'язання задач, що породжують експоненціальні алгоритми, пов'язане з повним перебором всіх можливих варіантів, і зважаючи на практичну неможливість реалізації такої стратегії, для їх розв'язання розробляються інші підходи.
Наприклад, якщо навіть існує експоненціальний алгоритм для знаходження оптимального розв'язку деякої задачі, то на практиці застосовуються інші, ефективніші поліноміальні алгоритми для знаходження не обов'язково оптимального, а лише прийнятного розв'язку (наближеного до оптимального). Але навіть якщо задача допускає розв'язання за допомогою поліноміального алгоритму, його можна побудувати лише після глибокого вникання в суть поставленої задачі.
Лекція 2

Теорія алгоритмів
Нотація великого О
Час, який витрачається алгоритмом, як функція розміру задачі
називається часовою складністю алгоритму.
Аналогічно можна визначити ємнісну складність (ємність
пам'яті, потрібну для вирішення задачі як функцію розміру
задачі).
Говорять, що час виконання програми (часова складність) має порядок T(n) від вхідних даних розміру n.
Наприклад, часова складність деякої програми T(n)= cn2, де с - деяка константа. Зауважимо, що розмір n - це завжди ціле додатнє число або нуль. Проте для багатьох програм час виконання дійсно є функцією вхідних даних, а не їхнього розміру.
Лекція 2

Теорія алгоритмів
Асимптотична складність алгоритмів
Поведінка часової (ємнісної) складності в границі при
збільшенні розмірності задачі називається асимптотичною
тимчасовою (ємнісною) складністю
Саме асимптотична складність алгоритму визначає у
результаті розмір завдання, яке можна вирішити цим
алгоритмом. Для опису асимптотичної швидкості зростання
функцій використовується O-символіка. Якщо говорять, що
час виконання T(n) деякої програми має порядок O(n2)
(читається “о велике від n в квадраті”), то мається на увазі, що
існує додатна константа с і розмір n0 такі, що при всіх n≥ n0 виконується нерівність T(n) ≤сn2.
Лекція 2

Теорія алгоритмів
Швидкість зростання функцій
Розглянемо функції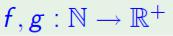 (f (n) і g (n) можна представляти собі як час роботи двох алгоритмів на входах розміру n).
(f (n) і g (n) можна представляти собі як час роботи двох алгоритмів на входах розміру n).
• Говоримо, що f росте не швидше за g, і пишемо f = O (g), якщо знайдуться такі константи c> 0 і n0, що 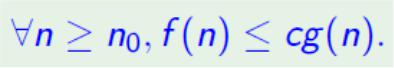
•Говоримо, що f росте не повільніше g, і пишемо f = Ω(g), якщо g = O(f ).
•Говоримо, що f і g мають однаковий порядок росту, і пишемо f = Θ(g), якщо f = O(g) і g = O(f ).
Лекція 2
Теорія алгоритмів
Велике О()
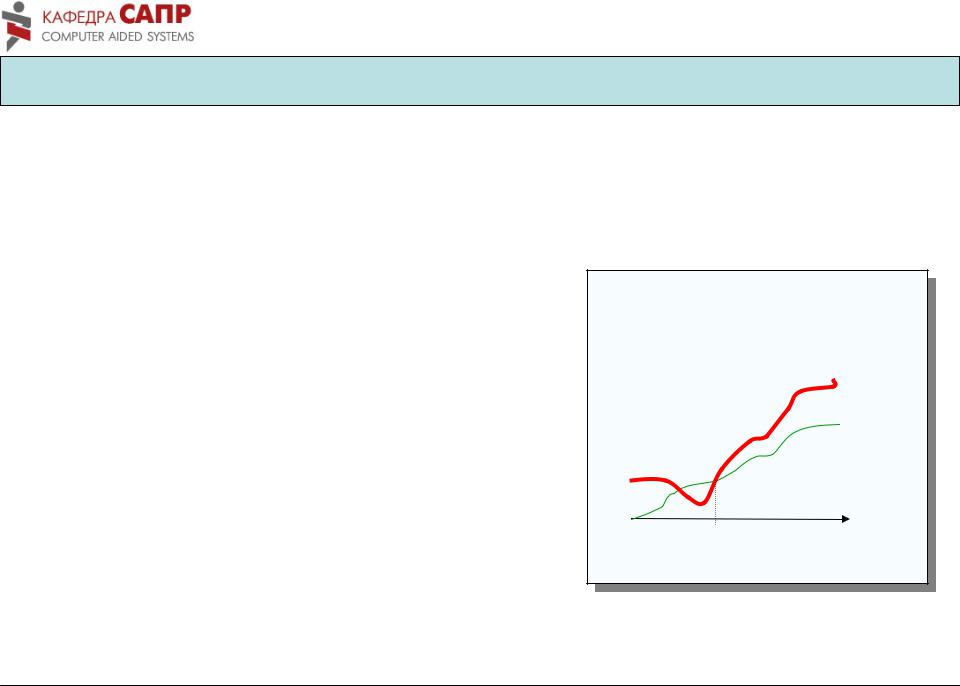
• Говоримо, що f росте не швидше за g, і пишемо f = O
(g), якщо знайдуться такі константи c> 0 і n0, що
Час виконання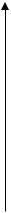
c g(n) f (n)
n0 Розмір вхідних даних
Лекція 2
Теорія алгоритмів
Велике Ω()
• Говоримо, що f росте не повільніше g, і пишемо
f = Ω(g), якщо g = O(f ).
Лекція 2
Час виконання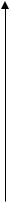
f (n)
c g(n)
n0 Розмір вхідних даних
Теорія алгоритмів
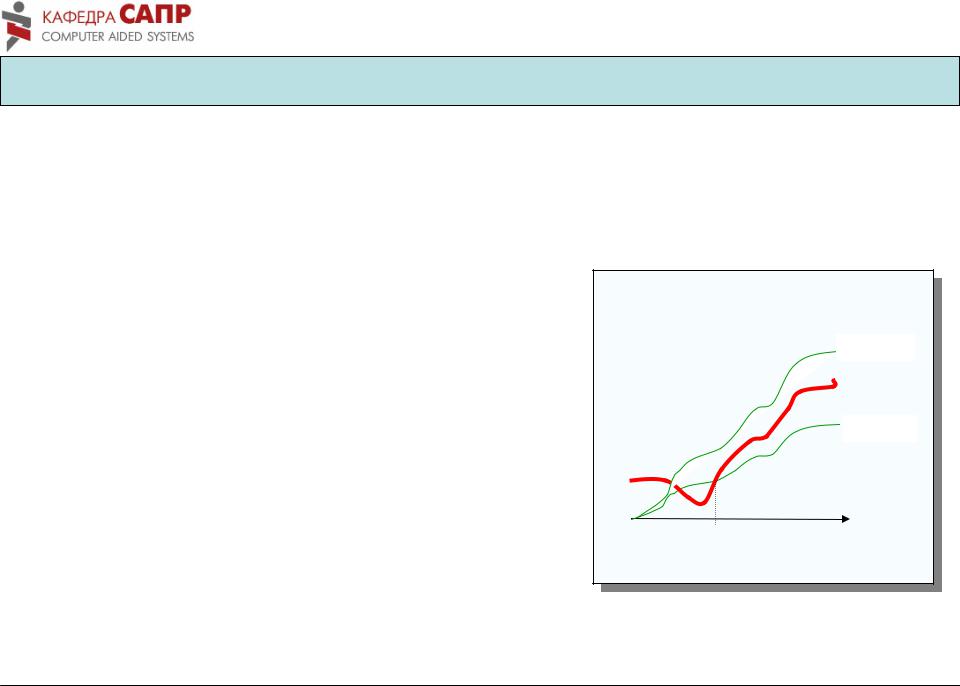
Велике Θ()
• Говоримо, що f і g мають однаковий порядок росту, і пишемо f = Θ(g), якщо f = O(g) і g = O(f ).
Лекція 2
Час виконання
c2 g(n)
f (n)
c1 g(n)
n0 Розмір вхідних даних

Теорія алгоритмів
Приклад: x2 проти 2x + 20
Якими б не були коефіцієнти, квадратична функція завжди обжене лінійну.
Лекція 2
Теорія алгоритмів
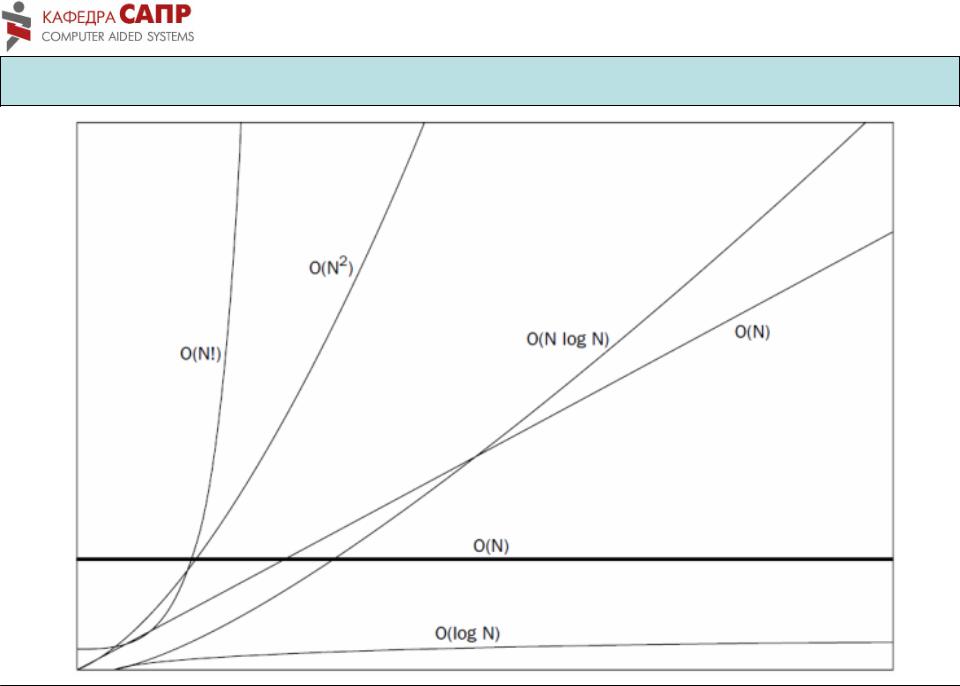
Графіки функцій
Лекція 2
