Фізика, частина 1

Фізичні основи механіки

Введемо позначення

mk 02 , mr 2 ,

де – коефіцієнт згасання, а 0 – власна частота з якою здійснювались би вільні коливання за відсутності опору середовища.

Тоді другий закон Ньютона можна записати у вигляді

x 2 x 02 x 0 .

Для розв’язання цього рівняння введемо нову змінну u, яка зв’язана з x

співвідношенням x e tu . Звідси

x и e t и e t ,

x и e t 2 и e t 2и e t .

Підставивши ці значення x і x в рівняння другого закону Ньютона для згасаючих

коливань і скорочуючи всі доданки на множник e t , отримуємо

и 02 2 и 0 .

Нехай опір середовища малий і 02 2 . Тоді можна ввести позначення

2 02 2 0 .

Врезультаті отримуємо рівняння

и 2и 0 ,

розв’язок якого має такий вигляд

u A0 cos t ,

де A0 і – сталі, які визначаємо з початкових умов. Отже, x A0 e t cos t ,

де A A0e t - амплітуда загасаючих коливань, а A0 - початкова амплітуда. Амплітуда згасаючих коливань зменшується з плином часу і тим скоріше, чим більший коефіцієнт опору і чим менша маса m коливного тіла.

дисипативної системи. Графік залежності x від часу наведений на рис. 36.

t

A0

Рис. 36

49

Фізичні основи механіки

Згасаючі коливання – неперіодичні коливання, бо в них ніколи не повторюються,

наприклад, максимальні значення зміщення, швидкості і прискорення. Однак при згасаючих коливаннях величина x перетворюється в нуль, змінюючись в один і той самий бік, а також досягає максимальних і мінімальних значень через однакові проміжки часу:

Величину T тому називають періодом згасаючих коливань.

Якщо A t і A t T – амплітуди двох послідовних коливань, що йдуть одне за одним

через проміжок часу T, то відношення

називається декрементом згасання, а його натуральний логарифм

æ ln D T

– логарифмічний декремент згасання.

якого амплітуда зменшується в e разів. Час називається часом релаксації.

Нехай N – кількість коливань, після яких амплітуда коливань зменшується в e разів.

Тоді

Логарифмічний декремент згасання æ є фізична величина, обернена до кількості коливань N, після закінчення яких амплітуда зменшується в e разів.

Добротністю коливальної системи називається величина Q , яка дорівнює добутку

2 на відношення енергії E t коливальної системи в довільний момент часу t до зменшення цієї енергії за проміжок часу від t до t+T:

Оскільки енергія E t пропорційна до квадрата амплітуди коливань, то

50

Фізичні основи механіки

Тут враховано, що при æ<<1 0 і умовний період Т згасаючих коливань практично дорівнює періоду T0 вільних коливань.

§18. Диференціальне рівняння вимушених коливань і його розв’язання. Резонанс

Розглянемо коливання, що їх здійснює система, якщо на неї, крім пружної сили kx і

сили опору rx , діє ще додаткова періодична сила F, яку називатимемо вимушуючою силою і

яка змінюється за гармонічним законом

F F0 cos t .

Диференціальне рівняння вимушених коливань, що відбувається вздовж осі OX, має такий вигляд:

mx kx rx F0 cos t ,

1

зменшується, амплітуда вимушених коливань зростає, доки не досягне значення A.

X

0

t

Рис. 37

Отже, усталені вимушені коливання системи, які виникають під дією сили F, також є гармонічними, тобто

51

Фізичні основи механіки

x Acos t ,

A 02 cos t f0 cos t .

Зцього рівняння видно, що амплітуда A і фаза повинні мати такі значення, щоб

52

Фізичні основи механіки

і, відповідно,

співвідношення між циклічними частотами вимушуючої сили і вільних коливань системи

0 .

відбувається, коли

53

Фізичні основи механіки

Виконуючи диференціювання, отримуємо

4 02 2 8 2 0 .

Це рівняння має два розв’язки: 0 , 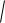02 2 2 . Розв’язок 0 відповідає максимуму знаменника виразу для A. Із інших двох розв’язків лише додатний має фізичний сенс.

Отже, резонансна частота – частота, при якій амплітуда A коливань досягає

максимального значення, – має такий вигляд.

54

Фізичні основи механіки

вимушуюча сила мають однакові фази; у всіх інших випадках 0 . Залежність від при

коливальної системи майже протилежна до фази зовнішньої вимушуючої сили.

ТИМОШЕНКО СТЕПАН ПРОКОПОВИЧ

(1878-1972)

Опублікував наукову працю „До питання про явища резонансу у валах”, в якій ідею наближеного розрахунку частот коливань застосував для розрахунку вала з кількома дисками по довжині.

§19. Утворення хвиль в пружному середовищі. Поздовжні і поперечні хвилі. Рівняння біжучої хвилі

Розглянемо пружне середовище, між частинками якого існують сили взаємодії, що перешкоджають тому або іншому виду його деформації. Тіло, яке коливається в пружному середовищі, періодично діє на прилеглі до нього частинки середовища, виводячи їх з положення рівноваги і змушуючи здійснювати вимушені коливання. При цьому середовище поблизу тіла деформується і в ньому виникають пружні сили. Ці сили діють як на прилеглі до тіла частинки, намагаючись повернути їх у положення рівноваги, так і на віддаленіші від тіла частинки, виводячи їх з положення рівноваги. Віддаленіші від тіла області середовища поступово втягуються в коливальний рух.

Процес поширення коливань в суцільному середовищі, яке неперервно розподілене в просторі і має пружні властивості, називається механічним хвильовим процесом, або механічною хвилею.

При поширенні хвилі частинки середовища не рухаються разом з хвилею, а

коливаються біля своїх положень рівноваги. Основна властивість всіх хвиль є перенесення

енергії без перенесення речовини.

Пружними (або механічними) хвилями називаються механічні збурення, що поширюються у пружному середовищі. Пружні хвилі бувають поперечні і поздовжні.

Рис. 41а

У поперечних хвилях частинки середовища коливаються в площинах, які перпендикулярні до напрямку поширення хвилі (рис. 41а). Поперечні хвилі можуть поширюватись в середовищі, в якому виникають пружні сили при деформації зсуву, тобто лише у твердих тілах.

Рис. 41б

55

Фізичні основи механіки

У поздовжніх хвилях частинки коливаються в напрямку поширення хвилі (рис. 41б). Ці хвилі можуть поширюватись в середовищах, в яких виникають пружні сили при деформації стиску і розтягу, тобто у твердих, рідких і газоподібних тілах.

Пружна хвиля називається гармонічною, якщо відповідні їй коливання частинок середовища є гармонічними.

Нехай поперечна гармонічна хвиля поширюється вздовж осі ОХ.

На рис. 42 наведена гармонічна хвиля (поперечна або поздовжня), яка поширюється вздовж осі ОХ зі швидкістю , тобто наведена залежність зміщень всіх частинок середовища, що беруть участь у хвильовому процесі, від відстані x цих частинок від джерела коливань O для якогось фіксованого моменту часу.

називається довжиною хвилі . Довжина хвилі дорівнює тій відстані, на яку поширюється певна фаза коливань за період:

Нехай точка, від якої йдуть коливання, коливається в суцільному середовищі.

Коливання поширюються від центра у всі боки.

Поверхня, до якої доходять коливання в деякий момент часу, називається фронтом

хвилі.

Фронт хвилі – це поверхня, яка відокремлює частину простору, уже залучену у хвильовий процес, від області, в якій коливання ще не виникли.

Поверхня, в якій всі частинки коливаються з однаковими фазами, називається

хвильовою.

Хвильову поверхню можна провести через довільну точку простору, який охоплений хвильовим процесом. Отже, хвильових поверхонь існує нескінченна множина, а хвильовий фронт в кожний момент часу лише один. Хвильові поверхні залишаються нерухомими, а

хвильовий фронт весь час переміщується.

Хвильові поверхні можуть бути довільної форми.

Хвиля називається плоскою, якщо її хвильові поверхні мають вигляд площин, які паралельні до площини, що проходить через джерело хвиль.

Хвиля називається сферичною, якщо її хвильові поверхні мають вигляд концентричних сфер. Центр цих сфер називається центром хвилі.

Напрямки, в яких поширюються коливання, називаються променями. В ізотропному середовищі промені перпендикулярні до фронту хвилі.

56

Фізичні основи механіки

Поширення в пружному середовищі механічних збурень, збуджених джерелом хвиль,

пов’язане з перенесенням хвилями енергії. Тому такі хвилі називаються біжучими хвилями.

Рівнянням хвилі називається вираз, який описує зміщення коливної частинки як функцію її рівноважних координат x, y, z і часу t.

Розглянемо плоску хвилю, яка поширюється вздовж осі OX і збуджується в площині x 0 (рис. 43). Нехай коливання в цій площині мають вигляд:

швидкість поширення хвилі. Отже, коливання частинок, що лежать у площині x, будуть запізнюватись на час від коливань частинок в площині x=0, тобто матимуть вигляд:

x,t Acos t 0

Введемо величину, яка називається хвильовим числом:

хвилі; 0 – початкова фаза коливань в площині x 0 . Величина Ф t kx 0 дорівнює фазі коливань в довільній площині з координатою х і називається фазою плоскої хвилі.

Зафіксуємо певне значення фази:

Продиференціюємо вираз для фази:

dt kdx 0 .

Звідси

dx . dt k 2 T

Отже, швидкість поширення хвилі є ніщо інше, як швидкість переміщення фази

хвилі і її називають фазовою швидкістю.

57

Фізичні основи механіки

Якщо плоска хвиля поширюється в довільному напрямку, то рівняння хвилі

де r – відстань від центра хвилі до точки середовища, яка розглядається. У випадку сферичної хвилі навіть у середовищі, яке не поглинає енергію, амплітуда коливань не

залишається постійною, а зменшується з відстанню за законом Ar . Це співвідношення справедливе лише для r, що значно більші за розміри джерела.

Рівняння довільної хвилі є розв’язком рівняння, яке називається хвильовим.

Для виведення цього рівняння використаємо рівняння плоскої хвилі, що поширюється

в довільному напрямку:

Acos t kx x k y y kz z 0 .

Продиференціюємо цю функцію двічі за кожною змінною:

Зіставимо цю суму з похідною за часом і врахуємо, що 2 2k 2 . Отже, поширення хвиль в однорідному ізотропному середовищі описується хвильовим рівнянням –

диференціальним рівнянням в частинних похідних:

58