Лабораторна робота №1

Тема роботи: ВИЗНАЧЕННЯ ЕНТРОПІЙНИХ ХАРАКТЕРИСТИК ОБ’ЄКТІВ КОМП’ЮТЕРНИХ МЕРЕЖ .

Мета роботи: навчитися визначати ентропії джерела інформації, приймача, каналу зв’язку, системи взаємозв’язаних об’єктів.

Теоретичні відомості

Ентропія джерела інформації Х, що генерує незалежні повідомлення x_i, обчислюється за формулою:

, (1)

де p(x_i)- ймовірність появи повідомлення x_i; N - кількість можливих повідомлень (символів, станів об’єкту)

Властивості ентропії

• Ентропія завжди невід’ємна: .

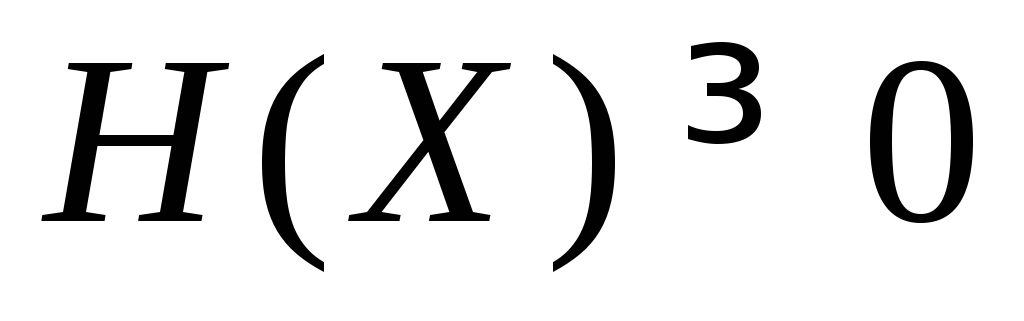• Ентропія максимальна, коли значення x_i випадкової величини X рівноймовірні:

. (2)

• Максимальне значення ентропії

. (3)

Для полегшення обчислень ентропії використовують наведену у додатку 1 таблицю значень добутків

Розглянемо систему, що є об’єднанням двох статистично взаємозв’язаних об’єктів, наприклад, джерела Х з можливими станами x₁, x_i, x_n та приймача Y з можливими станами y₁, y_j, y_m...

Сумісна ентропія системи:

, (4)

де  ймовірність сумісної появи i-го стану в об’єкті X та j-го стану в об’єкті Y.

Якщо об’єкти X та Y незалежні, то сумісна ентропія дорівнює сумі ентропій окремих об’єктів:

. (5)

Ентропія об’єкту Y (приймача), знайдена за умови, що об’єкт Х згенерував повідомлення х_i, називається частковою умовною ентропією об’єкту Y. Її визначають за формулою:

(6)

де p(y_j/x_i)  ймовірність події y_j за умови, що в об’єкті X відбулася подія x_i або ймовірність того, що приймач прийме символ y_j за умови, що джерело передало символ x_i.

Середню або повну умовну ентропію об’єкту Y відносно об’єкту X називають просто умовною ентропією, позначають H(Y/X) і визначають за формулою:

. (7)

Для незалежних об’єктів

, (8)

. (9)

Формули (10) та (11) показують взаємозв’язок ентропії об’єкту, сумісної та умовної ентропій.

(10)

, (11)

де H(X)  ентропія (безумовна) об’єкту Х;

H(Y)  ентропія (безумовна) об’єкту Y;

H(X,Y) – сумісна ентропія;

H(Y/X)  умовна ентропія об’єкту Y відносно об’єкту Х;

H(X/Y)  умовна ентропія об’єкту X відносно об’єкту Y.

Через часткову і повну умовну ентропії описують інформаційні втрати при передачі даних в каналі зв'язку з завадами. Для цього застосовують так звані канальні матриці. В якості елементів канальної матриці звичайно використовують умовні ймовірності p(y_j/x_i) отримання приймачем Y символу y_j за умови, що джерелом Х був відправлений символ x_i. При цьому канальна матриця P(Y/X)має наступний вигляд:

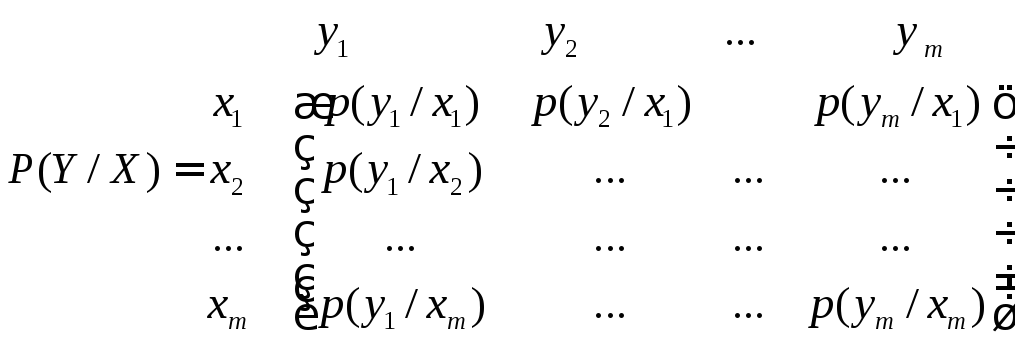. (12)

Ймовірності, що є елементами головної діагоналі матриці, описують ймовірність правильного прийому. Втрати, які мали місце при передачі сигналу x_i, описуються через часткову умовну ентропію:

(13)

Для обчислення всіх втрат при передачі всіх сигналів використовується умовна (повна) ентропія:

(14)

Для визначення ентропії приймача H(Y) за умови, що відома ентропія джерела H(X) і канальна матриця P(Y/X), необхідно знайти ймовірності появи символів на вході приймача p(y_j):

. (15)

Взаємозв'язок переданих і отриманих символів може бути описаний також матрицею сумісних ймовірностей P(X,Y):

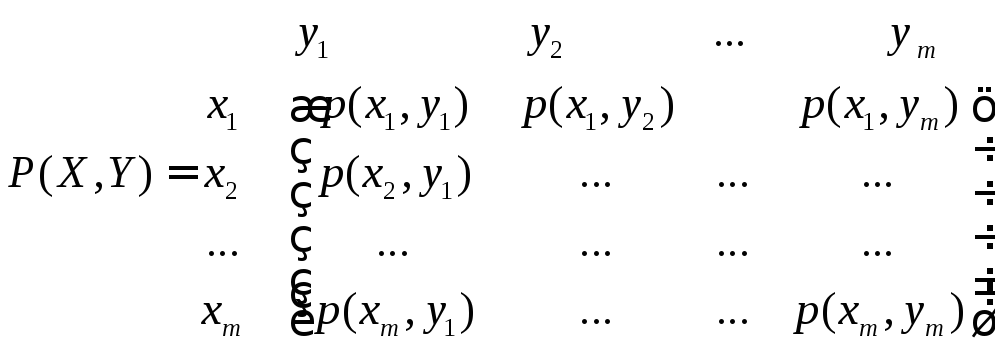. (16)

Сума всіх елементів стовпчика з номером j дає p(y_j), сума рядка з номером i дорівнює p(x_i), а сума всіх елементів матриці рівна 1. Сумісна ймовірність p(x_i, y_j) обчислюється таким чином:

. (17)

На практиці джерело Х найчастіше буває недоступне безпосередньому спостереженню, і його стан з’ясовується за допомогою деякого об’єкту Y, певним чином пов’язаного з об’єктом X. Для визначення кількості інформації I_Y->X, що міститься в об’єкті Y (приймачі) про об’єкт X (джерело) використовують взаємну ентропію H(Y->X).

Взаємна кількість інформації I_Y->X

I_Y->X = I_X->Y = I_Y<->X = I_{X<->Y =} H(Y->X) = H(X->Y) = H(X<->Y). (18)

Взаємна ентропія

. (19)

Формули (20) та (21) показують взаємозв’язок взаємної ентропії з іншими видами ентропій:

H(X<->Y) = H(Y) – H(Y/X) = H(X) – H(X/Y), (20)

H(X<->Y) = Н(Х) + Н(Y) – Н(Х, Y) = I_X->Y. (21)

Для ілюстрації формули (21) наведено рисунок, що дозволяє краще зрозуміти суть взаємної ентропії та взаємної кількості інформації.

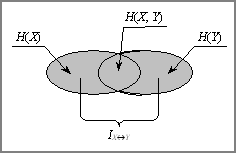
Рис.1 До визначення взаємної інформації.