8. Завдання до виконання
1. На множині A = {1,2,3} задані відношення впорядкованими парами елементів. Записати матричне представлення цих відношень.
a) {(1,2), (2,3), (3,2), (3,3)};
b) {(1,1), (1,2), (3,1), (3,2)};
c) {(1,2), (1,3), (2,1), (2,2)};
d) {(1,2), (1,3), (2,1), (2,2)};
e) {(1,1), (1,2), (1,3), (2,1), (2,2) , (2,3)};
f) {(1,3), (2,1), (2,3), (3,1), (3,2) , (3,3)}.
2. На множині A = {a,b,c} задані відношення впорядкованими парами елементів:
a) {(a,b), (b,b), (b,c), (c,a)};
b) {(a,a), (a,b), (b,a), (b,b)};
c) {(a,b), (a,c), (c,a), (c,b)};
d) {(b,a), (b,b), (b,c), (c,a)};
e) {(a,b), (a,c), (b,b), (b,c), (c,b) , (c,c)};
3. На множині А = {1,2,3}задано бінарні відношення:
,
,
.
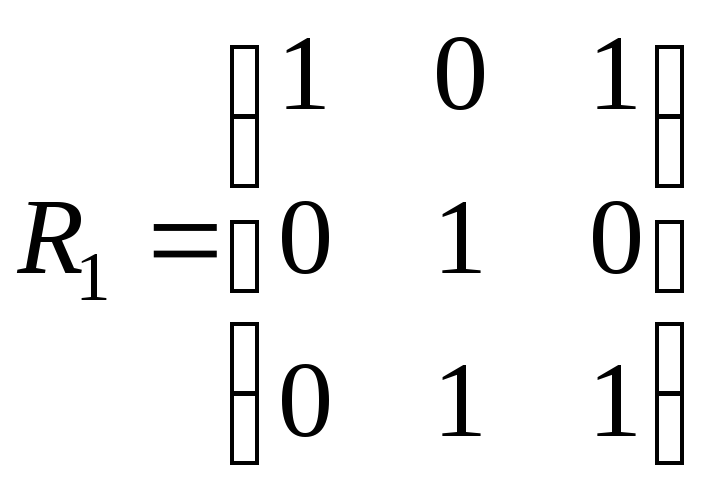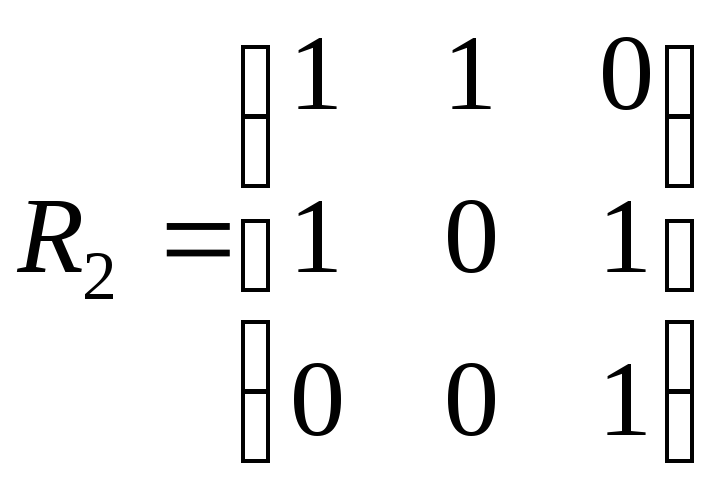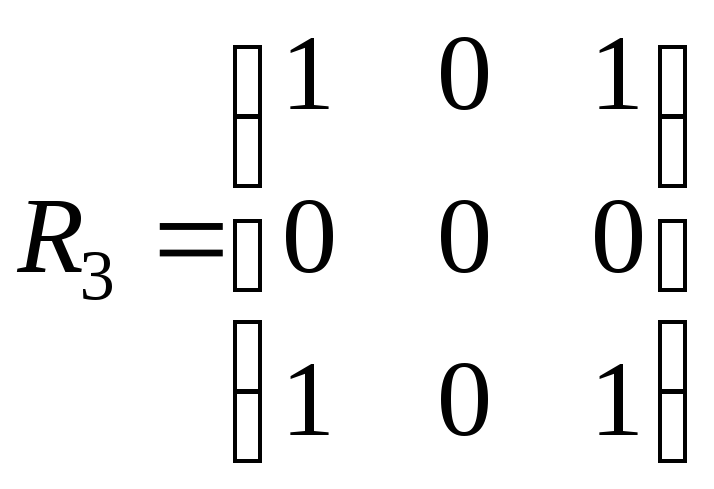Знайти представлення цих відношень у вигляді впорядкованих пар елементів.
4. На множині А = {с, f, k}задано бінарні відношення:
,
,
.
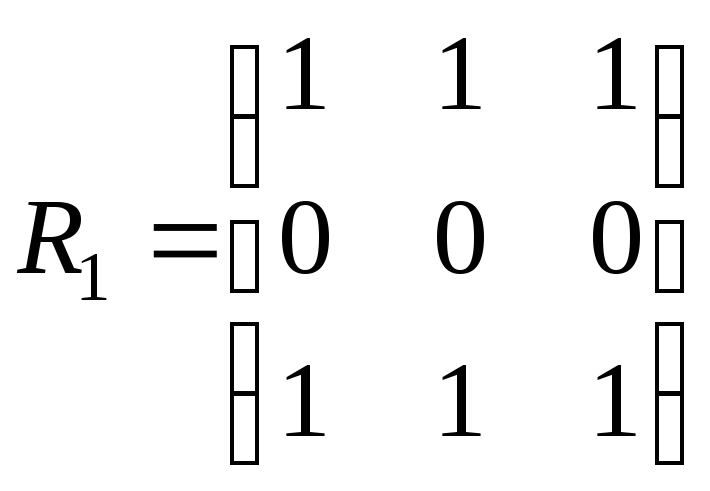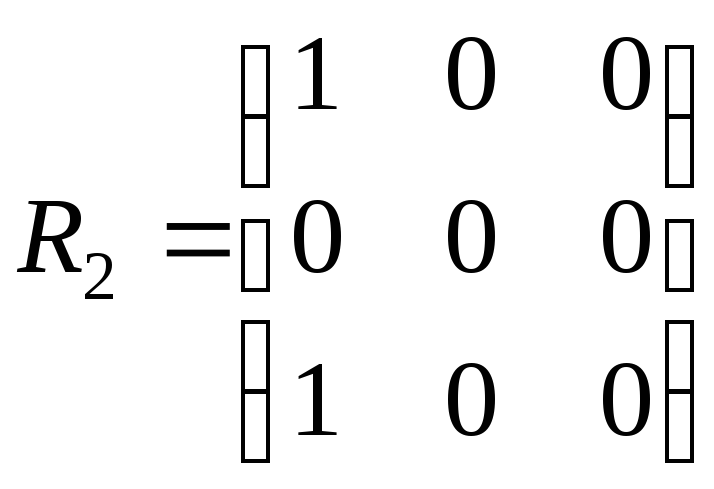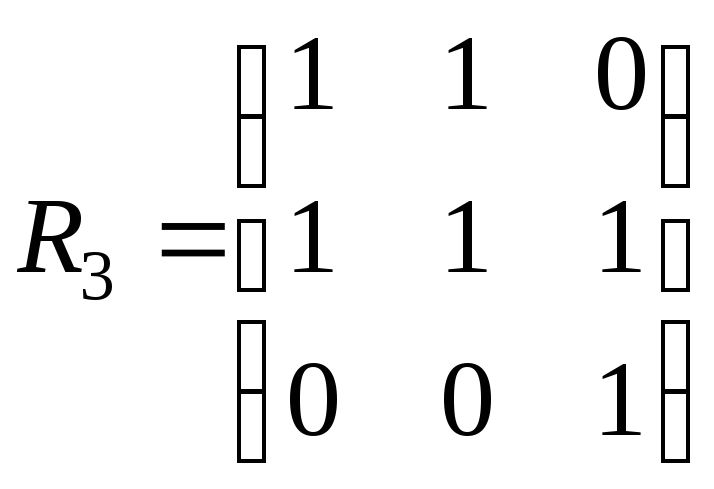Знайти представлення цих відношень у вигляді впорядкованих пар елементів.
5. Нехай відношення
задано матрицею:
.
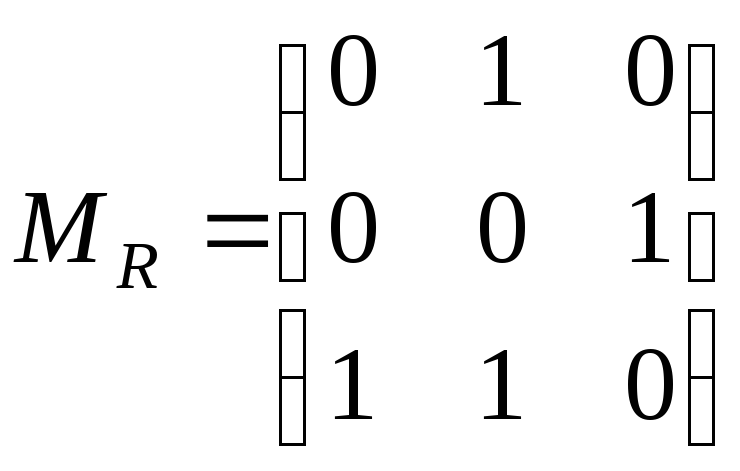Знайти матричне представлення a–b:
a)
;
б)
;
в)
г)
.
6. Знайти транзитивне замикання бінарного відношення “де використовується”, представленою таблицею фактів:
|
Конструкція |
Де використовується |
|
Болт |
Двигун |
|
Болт |
Колесо |
|
Гайка |
Двигун |
|
Гайка |
Колесо |
|
Двигун |
Автомобіль |
|
Колесо |
Автомобіль |
|
Вісь |
Колесо |
7. На множині А = {a, b, c} задано бінарні відношення:
=
{(a,b),
(b,b),
(b,c),
(c,a)};
={(a,a),
(a,b),
(b,a),
(b,b),
(c,a)};
={(a,b),
(a,c),
(b,c),
(c,c)}.Знайти
відношення:
\
,
\
,
,
,
,
,
,
,
.
,
,
,
,
,
,
,
,
.
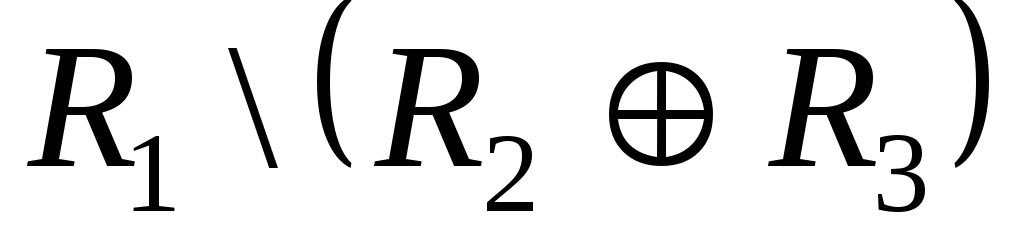
8. Відношення
означає“бути
старше”,
тобто запис x
y
означає “х
старший у”.
Визначте чи є відношення:
а) рефлексивне; б) іррефлексивне; г) симетричне;
д) асиметричне; е) антисиметричне; в) транзитивне.
9. Які відношення a-e на множині {a, b, c, d} є відношеннями еквівалентності? Відношеннями часткового порядку?
а) {(a, a), (b, b), (c, c), (d, d)};
б) {(a, a), (a,c), (c, a) ,(c, c), (c, d), (d,c), (d, d)};
в) {(a, a), (b,b), (b, c), (c, b), (c,c), (d, d)};
г) {(a, a), (b,b), (b, d), (c, c), (c, d), (d,b), (d,c), (d, d)};
д) {(a, a), (a,b), (a, c), (b, a), (b, b), (b,c), (c,a), (c, c), (d, d)};
е) {(a, a), (a,b), (a, c), (a, d), (b, b), (b,d), (c,d), (d,d)};
10. Які з матриць a–b зображають відношення еквівалентності:
а)
;
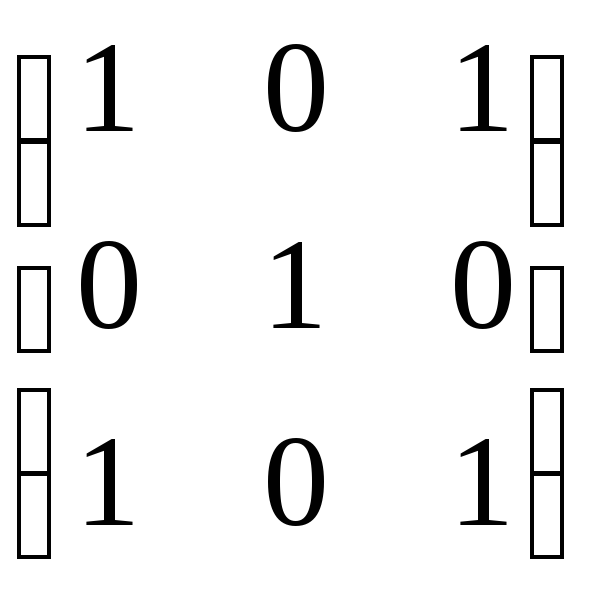б)
;
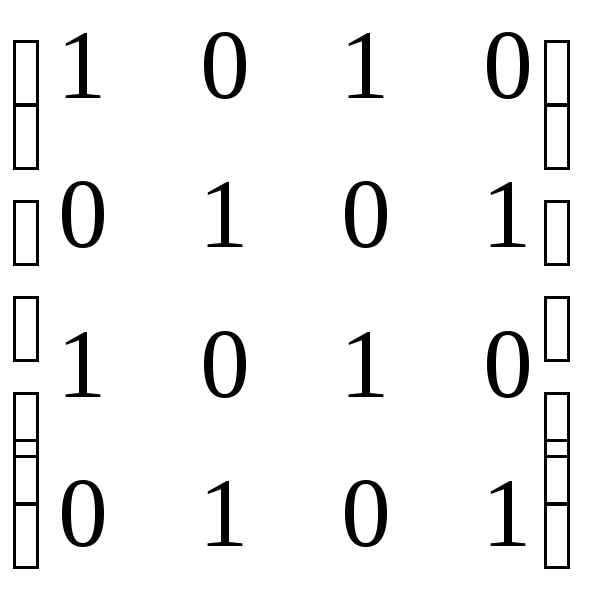в)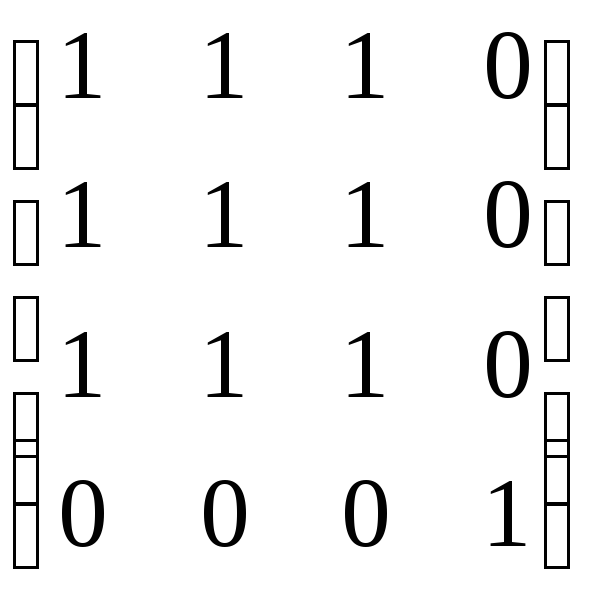
.
11. Які з матриць a–b зображають відношення часткового порядку:
а)
;
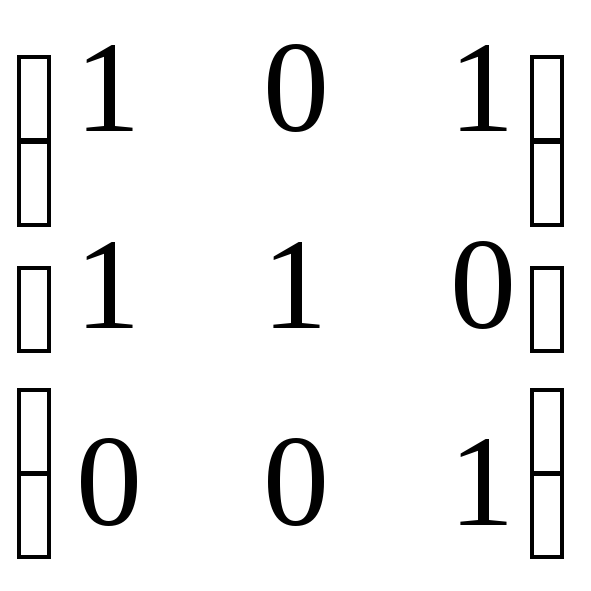б)
;
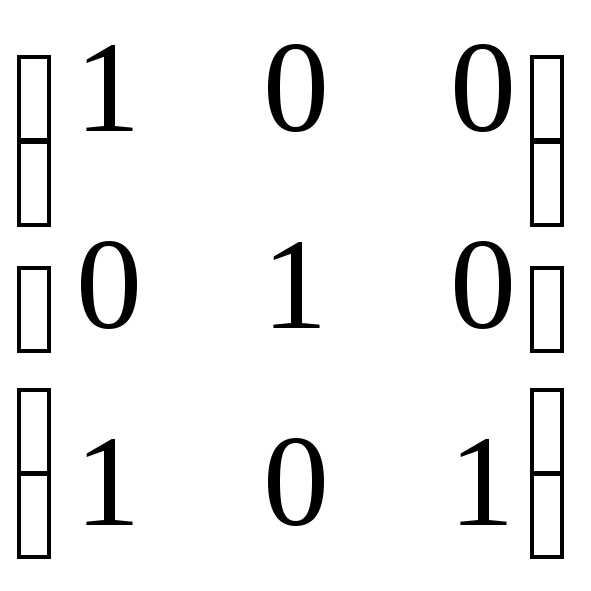в)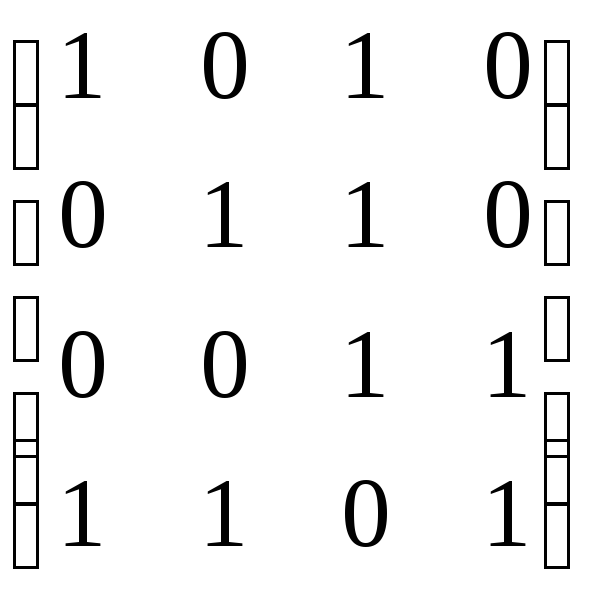
.
12. На множині А задано бінарні відношення:
,
,
.
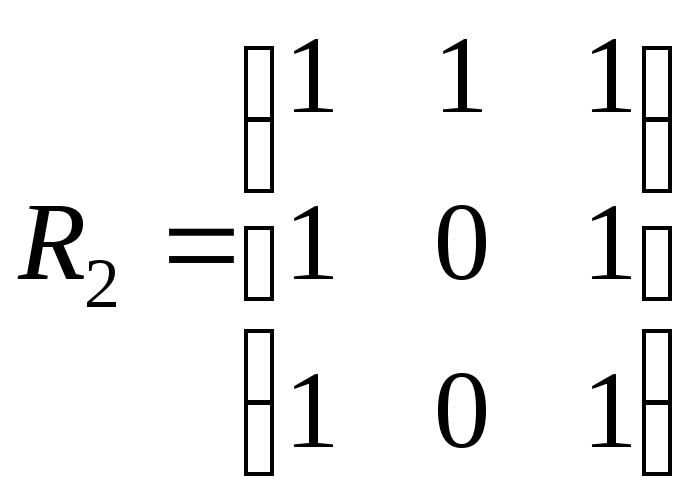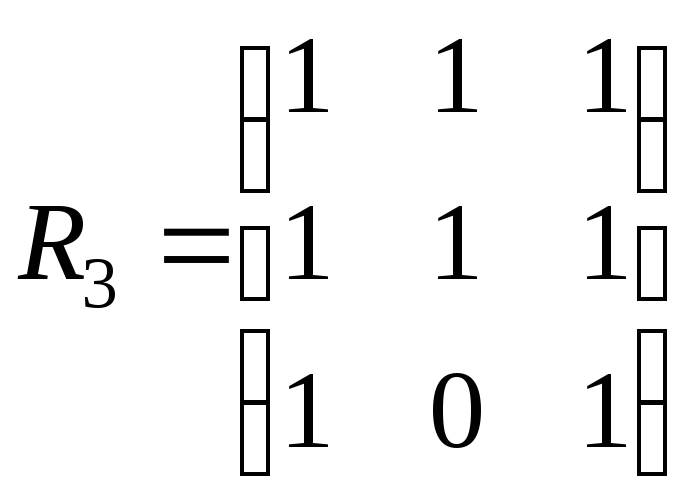Визначити, які з цих відношень:
а) рефлексивні; б) іррефлексивні; в) транзитивні;
г) симетричні; д) асиметричні; е) антисиметричні;
є) відношення еквівалентності;
ж) відношення часткового порядку.
13. Задано відношення
=
{(0, 1), (0, 3), (1, 1), (1, 3), (2,1) , (2,3), (3, 3)} на множині
{0, 1, 2, 3}. Визначити властивості відношення:
а) рефлексивне; б) іррефлексивне; в) транзитивне;
г) симетричне; д) асиметричне; е) антисиметричне;
є) відношення еквівалентності;
ж) відношення часткового порядку.
14. На множині А задано бінарні відношення:
,
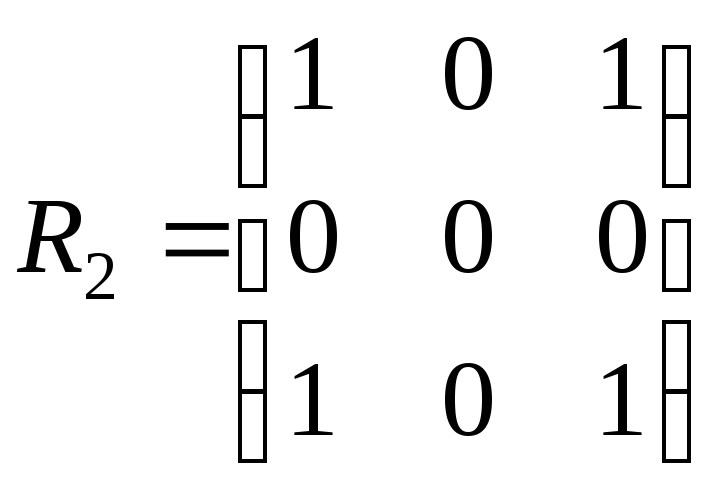,С
=
\
,D=
.
Визначити, які з цих відношень:
а) рефлексивні; б) іррефлексивні; в) транзитивні;
г) симетричні; д) асиметричні; е) антисиметричні;
є) відношення еквівалентності;
ж) відношення часткового порядку.
15. На множині А = {a,b,c} задано бінарні відношення:
,
,
,
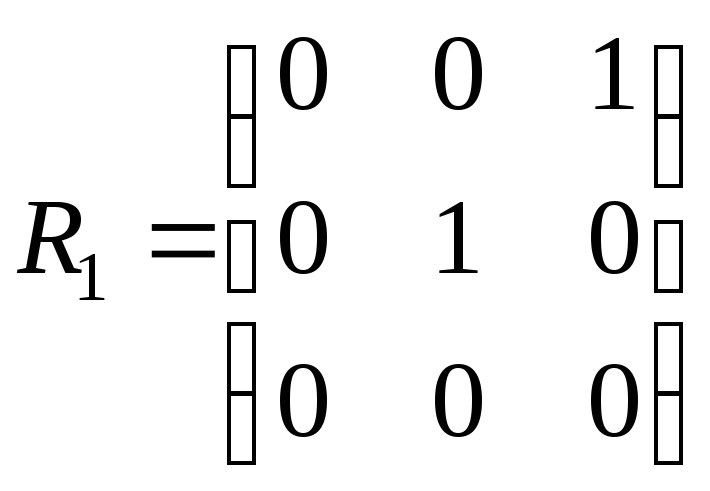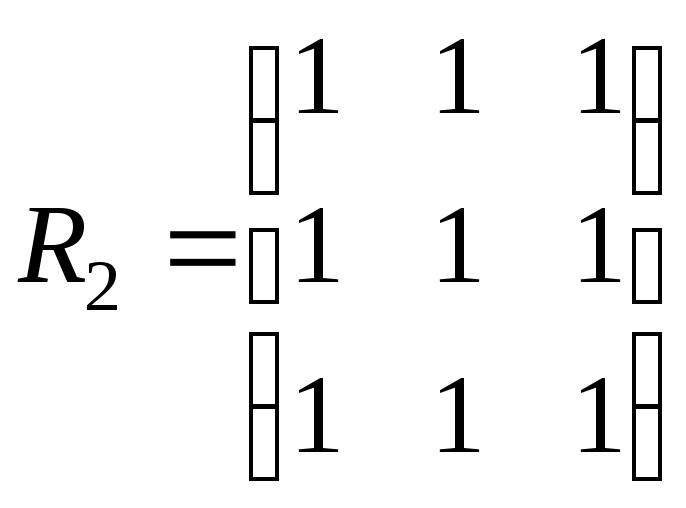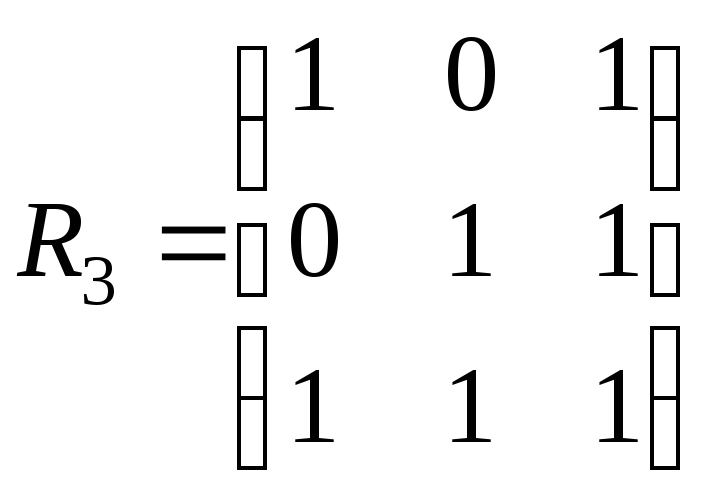A =
,
B =
.
Визначити, які з цих відношень:
а) рефлексивні; б) іррефлексивні; в) транзитивні;
г) симетричні; д) асиметричні; е) антисиметричні;
є) відношення еквівалентності;
ж) відношення часткового порядку.
16. На множині А={1,2,3} задано відношення :
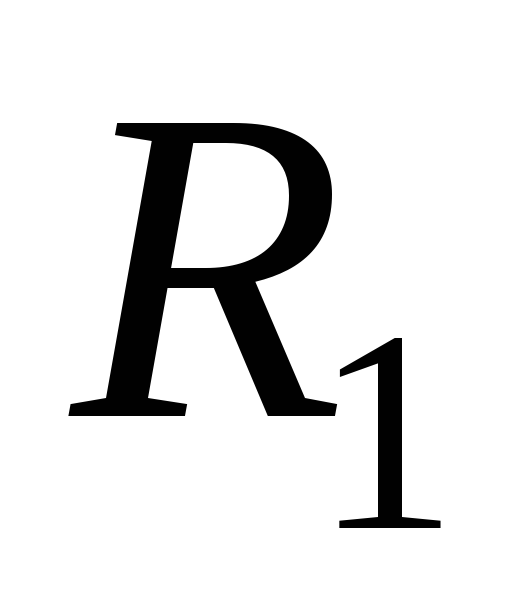={(1,2),
(2,3), (3,2), (3,3)};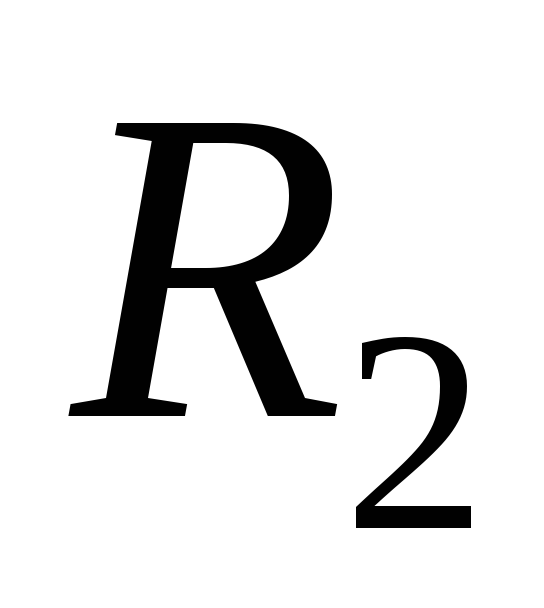
={(1,2),
(2,2), (2,3), (2,1), (3,1)};
={(1,1),
(1,2), (1,3), (2,2), (3,3) }. D =
.
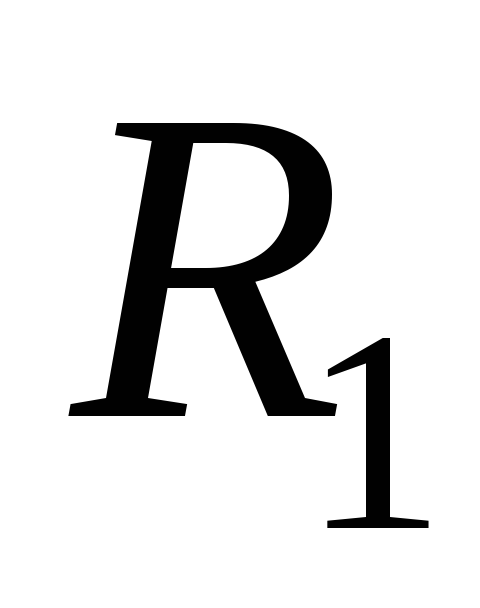
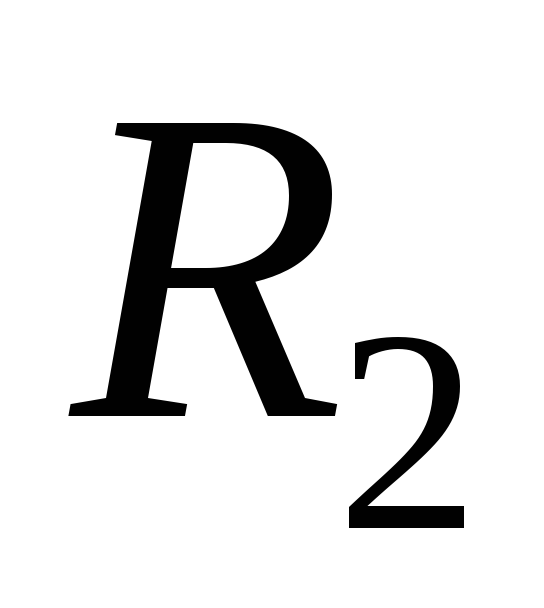
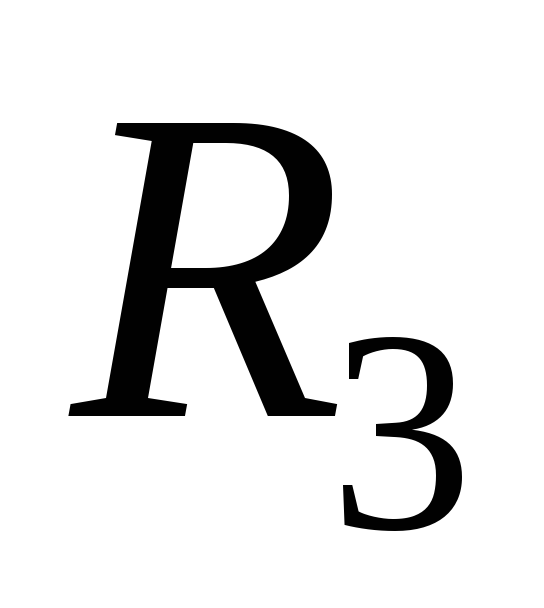Визначити, які з цих відношень:
а) рефлексивні; б) іррефлексивні; в) транзитивні;
г) симетричні; д) асиметричні; е) антисиметричні;
є) відношення еквівалентності;
ж) відношення часткового порядку.
17. Якими властивостями володіє бінарне повне відношення? Тотожнє відношення? Бінарне порожнє відношення?
18. Знайти найменше
відношення на множині {1, 2, 3, 4}, яке містить
відношення
={(1,2),
(1,4), (3,3), (4,1)} і таке, що є:
а) рефлексивним і транзитивним;
б) симетричним і транзитивним;
в) рефлексивним, симетричним і транзитивним.
19. Написати програму на мові С++, яка б визначала, чи має відношення властивість рефлективності. Відношення задається матрицею, яка вводиться з клавіатури. Що потрібно змінити, щоб перевірити іррефлексивність ?
20. Написати програму на мові С++, яка б визначала, чи має відношення властивості: симетричне, асиметричне, антисиметричне.
21. Написати програму на мові С++, яка б визначала, чи є відношення, задане матрицею, транзитивним відношенням.
22. Написати програму на мові С++, яка б визначала, чи є відношення, задане матрицею, відношенням часткового порядку.
23. Написати програму на мові С++, яка б визначала, чи є відношення, задане матрицею, відношенням еквівалентності.
24. Хай
на множині
задано відношення
:
"х
знайомий з у".
Чому не можна розбити множину
на класи еквівалентності?
а) відношення
не рефлексивне;
б) відношення
не симетричне;
в) відношення
не транзитивне.
25. Задано відношення
R
={(1,2), (1,4), (3,3), (4,1)} на множині A
= {1,2,3,4}. Яке
повинне бути відношення S
щоби композиція
була транзитивним відношенням?
26. Знайти
обернені відношення до відношень
={(1,3), (2,2), (3,2), (3,3)},
={(1,1), (1,2), (1,3), (3,3)},
={(2,1), (2,2), (2,3), (3,1)} заданих на множині A
= {1, 2, 3}.
27. Якими властивостями володітиме обернена матриця:
а) рефлексивного відношення; б) іррефлексивного відношення;
в) транзитивного відношення; г) симетричного відношення;
д) асиметричного відношення; е) антисиметричного відношення.
28. Чи вірні твердження:
а)
;
б)
;
в)
;
д)
.
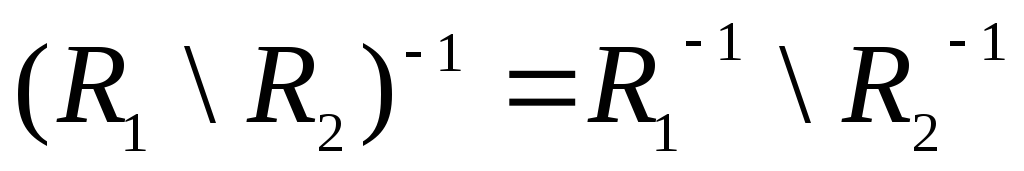