2.4.Опис алгоритму моделювання

Задамо три масиви: масив каналів, масив черги і масив сумарного часу перебування у відповідному стані. У перший будемо заносити час обслуговування 1/, в комірку відповідну номеру вільного каналу в момент приходу заявки на обслуговування; у другий одиницю, при зайнятому відповідному місці в черзі чи нуль при його звільненні.

Алгоритм моделі системи наступний:

1. Випадковим образом генеруємо деяку величину  - часовий інтервал між попередньою і поточною заявками, які потрапили на обслуговування, але так щоб її математичне очікування було рівним .

2. У циклі пройдемо часовий інтервал від T до T+, де T - час від початку роботи системи до моменту приходу наступної заявки з дискретністю , зменшуючи значення в масиві каналів на величину  .

3. Після кожного проходу підрахуємо кількість комірок у масиві каналів і масиві черги значення яких більше нуля (зайнятих) і збільшимо комірку відповідну цьому числу на  .

У випадку звільнення якогось з каналів, він займається заявкою з черги, при наявності останньої, а черга зсовується.

4. Після проходу всього циклу знову заявку, яка потрапила на обслуговування поміщаємо у вільний канал, при його наявності, чи в чергу, при наявності місця в ній. Інакше заявка одержує відмовлення, збільшуючи тим самим лічильник відмовлень на одиницю.

5. Повторюємо пункти 1-5 поки час T не досягне заданого значення.

Не секрет , що моделювання даної системи було б не повним без фактора випадковості надходження заявок у систему. Для реалізації цього в програму включений генератор випадкових чисел, що генерує псевдо-випадкові послідовності. Алгоритм його роботи полягає в наступному: нехай є декілька цілих, позитивних чисел n₀, m, L, M. Тоді кожне наступне число будемо знаходити по формулі:

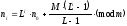(2.12)

Отримана послідовність має рівномірний розподіл.

Недоліком є те, що всі одержувані числа цілі, а це не завжди зручно. Числа від 0 до 1 зручні тим, що з таких чисел легко отримати числа будь-якого діапазону. У нашому випадку нам необхідно згенерувати послідовність так, щоб її математичне очікування дорівнювало інтенсивності надходження . Для досягнення цього почнемо наступний прийом:

підберемо n₀, m, L, M так, щоб отримувані числа були більші 1000;

потім перевизначимо n_i таким чином:

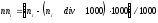(2.13)

де div - ціла частина від ділення. Тепер, для одержання випадкової послідовності з математичним очікуванням , необхідно помножити n_i на 2*, тому що математичне очікування рівномірно розподіленої випадкової величини дорівнює 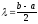, деb і a відповідно кінець і початок інтервалу розподілу; прийнявши a = 0 , отримаємо b = 2*.

Пошук числа реалізацій здійснюється по методу Монте-Карло, основаному на центральній граничній теоремі. Відповідно до цієї теореми, при великому числі опитів N частота появи події A прагне до його імовірності. Аналітично це має наступний вид:

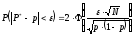(2.14)

Задамося яким-небудь досить близьким до одиниці значенням імовірності Q і назвемо його «рівнем довіри». Якщо імовірність того, що частота й імовірність розходяться менше чим на , буде Q чи більше, будемо вважати задачу розв’язаною. На практиці рівень довіри Q вибирається близьким до одиниці. Припустимо, що імовірність Q задана, тоді прирівнюючи Q до правої частини (2.14) отримаємо:

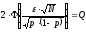(2.15)

тепер виразимо N:

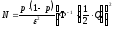(2.16)

це і є формула для розрахунку числа реалізацій.