1.3 Класифікація систем масового обслуговування

Системи масового обслуговування класифікуються за різноманітними ознаками. На рис. 1.1 зображена узагальнена схема класифікації СМО за різними ознаками:

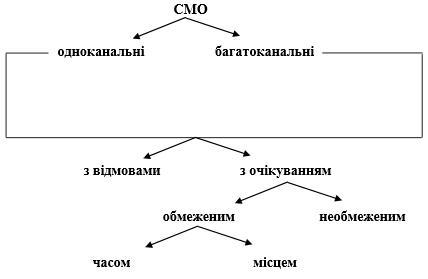
Рис. 1.1 – Класифікація систем масового обслуговування

Класифікація СМО за складом:

• одноканальні (з одним обслуговуючим пристроєм);

• багатоканальні (з декількома паралельними обслуговуючими пристроями).

За складом обслуговуючих пристроїв багатоканальні СМО поділяють на:

• однофазні (якщо після проходження одного обслуговуючого пристрою замовлення вважається обслуженим);

• багатофазні (замовлення повинно послідовно пройти через декілька обслуговуючих пристроїв).

Класифікація за часом перебування вимоги в системі до початку обслуговування:

• з відмовами (якщо замовлення, що надійшло до системи, не може бути обслужене, воно покидає систему);

• з очікуванням (замовлення, що надійшло до системи у момент, коли всі канали зайняті, становиться в чергу і очікує на обслуговування).

Очікування може бути обмеженим і необмеженим. Обмежуватись очікування може часом очікування або довжиною черги.

2. Основні відомості про задачу і метод її роз’язання

2.1 Перелік скорочень і основних термінів

Ми будемо використовувати наступні позначення:

• P_i - імовірність i-ого стану;

• P_від - імовірність відмовлення;

• a - абсолютна пропускна здатність системи;

• q - відносна пропускна здатність системи;

• t_оч - середній час очікування в черзі;

• m - число місць у черзі;

• λ - інтенсивність надходження заявок;

• μ - інтенсивність обслуговування;

• n - число каналів обслуговування;

• t_сист - середній час перебування в системі;

• N_реаліз - число реалізацій;

• T_реаліз - час реалізації;

• ε - точність;

• Q - рівень довіри;

• τ - часовий інтервал між заявками;

• СМО - система масового обслуговування.

2.2.Постановка задачі

Постановка задачі така: є n каналів обслуговування і m місць у черзі, інтенсивність надходження заявок  і інтенсивність обслуговування  . Необхідно теоретично і практично розрахувати:

• P_i - імовірності станів,

• P_отк - імовірність відмовлення,

• a - абсолютну пропускну здатність системи,

• q - відносну пропускну здатність системи,

• t_оч -середній час чекання в черзі,

• t_сист - середній час перебування в системі,

• N_реаліз - число реалізацій для досягнення імовірності відмовлення відмінної від теоретичної на величину  .

Теоретичний розрахунок представляє собою обчислення вище приведених величин згідно формул для випадку, коли розподілення часу надходження заявок підкоряється Пуаcсоновському закону розподілення. Необхідні формули і їхній вивід будуть розглянуті нижче в цьому розділі.

У практичній частині необхідно побудувати модель системи, за умови, що час надходження заявок підкоряється рівномірному закону розподілення, і розрахувати вище описані величини. Слід зазначити, що теоретичний розрахунок параметрів системи для випадку, коли потоки подій переводять систему зі стану в стан розподілені за законом відмінному від Пуасcоновського, досить складний. Аналітичні формули в цьому випадку для характеристик СМО вдається одержати тільки для найпростіших випадків. Таким чином пошук необхідних величин за допомогою моделювання є самим оптимальним рішенням.