
elem_mat / lishnee iz lekcii 11
.docВідзначимо попутно, що дроби виду
![]()
часто
зустрічаються в задачах на складання
рівнянь. У чисельнику і знаменнику
такого дробу стоять лінійні однорідні
вирази, що залежать від х
та
у.
Якщо
не розглядати випадок у = 0,
то
функція F (х, у)
залежить
фактично лише від однієї змінної, а
саме, від відношення
![]()

При цьому рівняння F (х, у) = C дозволяє знайти це відношення.
Задача. Три однакові пробірки наповнені до половини розчинами спирту. Після того як уміст третьої пробірки розлили нарівно в перші двох, об’ємна концентрація спирту в першій зменшилася на 20 % від первісної, а в другий збільшилася на 10 % від первісного значення. В скількох разів первісний об’єм спирту в першій пробірці перевищував первісний об’єм спирту в другій пробірці?

Рис. 3
Розв’язок. Введемо в розгляд об’єм половини пробірки V0 і концентрації розчинів спирту в кожній із пробірок c1 і с2. Тоді первісний об’єм спирту в першій пробірці дорівнює V0c1, у другій V0c2, у третій V0c3 (рис. 3). Для того щоб розв’язати задачу, підрахуємо об’єми спирту в першій і другій пробірках після того, як туди додадуть вміст третьої пробірки. Ці об’єми будуть рівні: у першій пробірці
![]()
у другій пробірці
![]()
Знайдемо нові концентрації спирту в цих пробірках. Для першої пробірки вона дорівнює
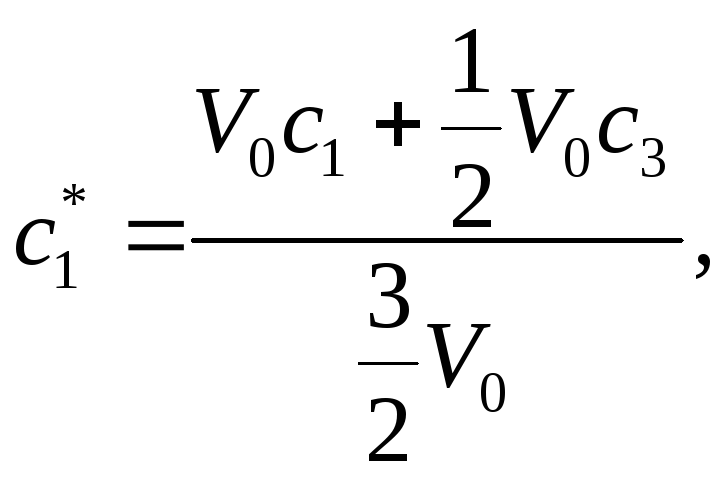
для другої
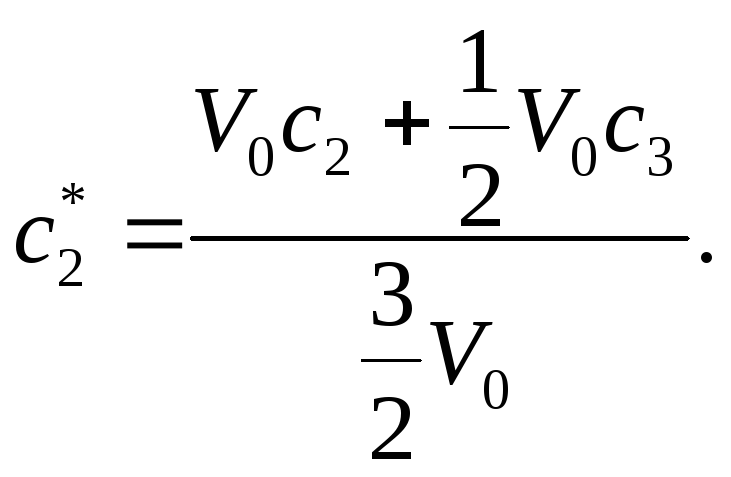
За умовою
задачі
![]() і
і
![]() Тоді маємо систему двох рівнянь з трьома
невідомими:
Тоді маємо систему двох рівнянь з трьома
невідомими:
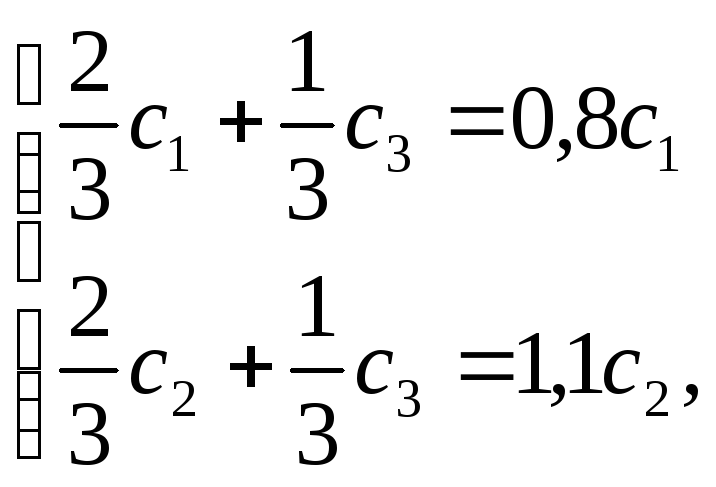
або
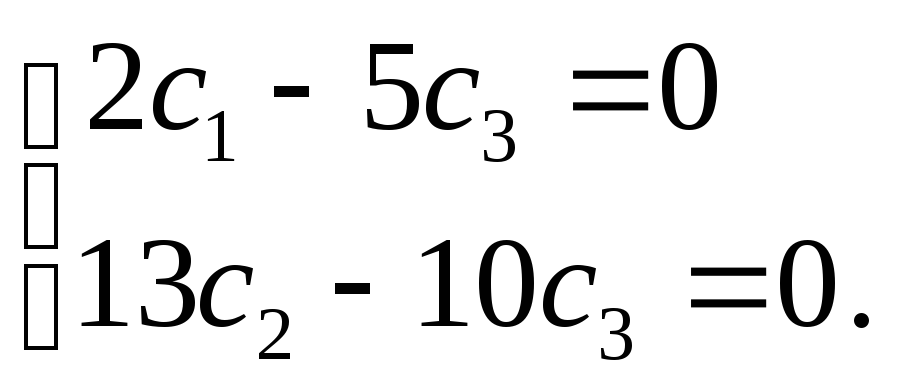
З цієї системи, так само як і в попередній задачі, не можна визначити всі три концентрації c1, c2 і с3. Але завдяки тому, що рівняння системи являють собою однорідні лінійні вирази, з неї можна знайти співвідношення двох концентрацій до третьої, наприклад с1/с3 і с2/с3:
![]()
![]()
Об’єм спирту в першій пробірці відноситься до об’єму спирту в другій пробірці як т/п. Дійсно,
![]()
Відповідь. У 3,25 рази.
Звернемося тепер до задач, які можна об’єднати в одну групу через те, що їхній розв’язок пов’язаний з виявленням загальної закономірності зміни тієї чи іншої величини в результаті багаторазово повторюваної операції.
Розглянемо наступний приклад.
У сосуді, об’єм якого дорівнює V0 л, міститься р %-й розчин солі (рис. 4). Із сосуду виливається а л суміші і доливається а л води, після чого розчин перемішується. Ця процедура повторюється п разів. Запитується, за яким законом змінюється концентрація солі в сосуді, тобто яка буде концентрація солі після п процедур?
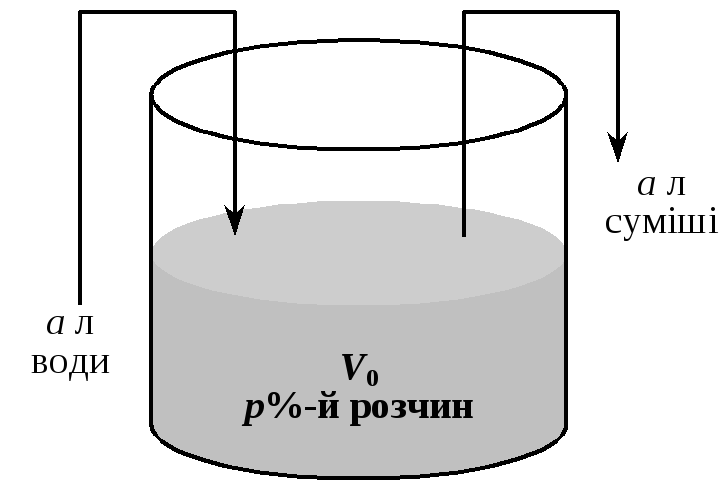
Рис. 4
Розв’язок. Очевидно, що первісний об’єм солі у розчині дорівнює
![]()
Після того як відлили а л суміші, у розчині залишилося
![]()
літрів солі, а її концентрація після додавання а л води дорівнює
![]()
Після того як відлили ще а л суміші (але вже з концентрацією c1), у розчині залишилося солі
![]()
а її концентрація після додавання а л води дорівнює
![]()
Немає потреби ще раз проробляти ту ж процедуру, щоб переконатися, що концентрація солі в розчині після п переливань визначається формулою
![]() (2)
(2)
що являє собою геометричну прогресію, що убуває. Множник
![]()
що є знаменником цієї прогресії, показує, у скільки разів убуває концентрація після чергового переливання.
Приклад 3. У кожному із двох сосудів знаходиться по V0 л кислоти однакової концентрації. З першого сосуду відлили а л розчину і долили а л води. Потім цю процедуру повторили ще раз. З другого сосуду відлили 2а л розчину і долили 2а л води. Потім цю процедуру повторили ще раз. Відомо, що концентрація кислоти в першому сосуді виявилася в 25/16 рази більшою, ніж концентрація кислоти в другому сосуді. Яку частину від об’єму сосуду складають а л?
Розв’язок. Використовуючи отримані вище результати, маємо
![]()
або
![]()
З цього рівняння знаходимо співвідношення a/V0. Знаходячи з обох частин рівняння арифметичний корінь, одержуємо
![]()
Оскільки a/V0 < 1 і 2а/V0 < 1, то
![]()
Звідси знаходимо шукане відношення:
![]()
Відповідь. 1/6 частина.
Наведемо
узагальнення формули (2) на випадок, коли
щоразу у сосуд доливається не вода, а
розчин тієї ж солі з постійною концентрацією
![]() ,
тобто
йдеться про наступну задачу: у сосуді
об’ємом V0
л
міститься р%-й
розчин солі. Із сосуду виливається а
л суміші і доливається стільки ж літрів
q%-го
розчину солі, після чого розчин
перемішується. Запитується, за яким
законом змінюється концентрація солі
в сосуді, тобто яка буде концентрація
після п
процедур?
,
тобто
йдеться про наступну задачу: у сосуді
об’ємом V0
л
міститься р%-й
розчин солі. Із сосуду виливається а
л суміші і доливається стільки ж літрів
q%-го
розчину солі, після чого розчин
перемішується. Запитується, за яким
законом змінюється концентрація солі
в сосуді, тобто яка буде концентрація
після п
процедур?
Остаточний розв’язок має вигляд

Для
доведення цієї формули позначимо
концентрацію розчину солі, що міститься
в сосуді після п
переливань,
через
![]() .
Тоді
після чергової
.
Тоді
після чергової
![]() -й
процедури, що полягає в тому, що виливають
а
л
розчину з концентрацією
-й
процедури, що полягає в тому, що виливають
а
л
розчину з концентрацією
![]() і
доливають
а
л
q
%-го
розчину, концентрація солі стає рівної
і
доливають
а
л
q
%-го
розчину, концентрація солі стає рівної
![]()
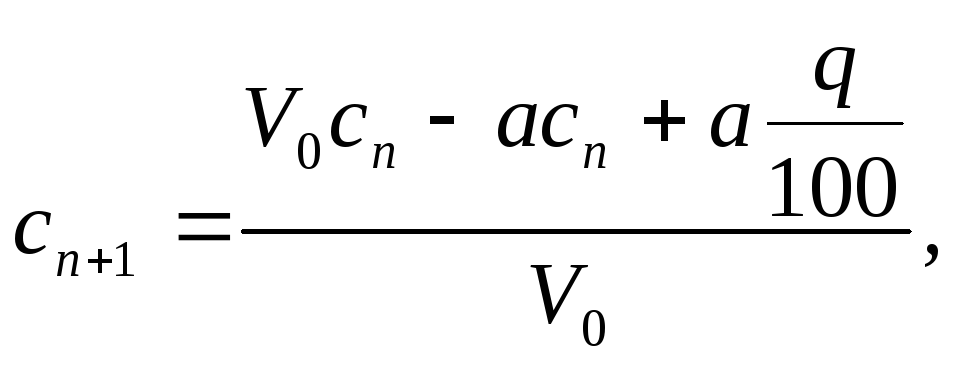
або
![]()
![]()
Спробуємо визначити концентрацію сп з отриманого співвідношення. При цьому будемо враховувати, що початкове значення концентрації відомо:
![]() при
при
![]()
Запишемо наступні дві рівності:
![]()
![]()
![]()
Віднімаючи ці вирази почленно один від одного, одержимо
![]()
Якщо
позначити різницю концентрацій
![]() через
через
![]() останню рівність можна переписати в
більш простому вигляді:
останню рівність можна переписати в
більш простому вигляді:
![]()
або
![]()
Звідси
видно, що послідовність чисел
![]() утворює геометричну прогресію зі
знаменником
утворює геометричну прогресію зі
знаменником
![]()
![]()
Перший член цієї прогресії легко визначається:

![]()
Після цього знаходимо
![]()
або
![]()
Запишемо останню рівність для значень п, рівних 1, 2, ... n, і додамо співвідношення, що виходять, між собою:
![]()
![]()
![]()
![]()

або
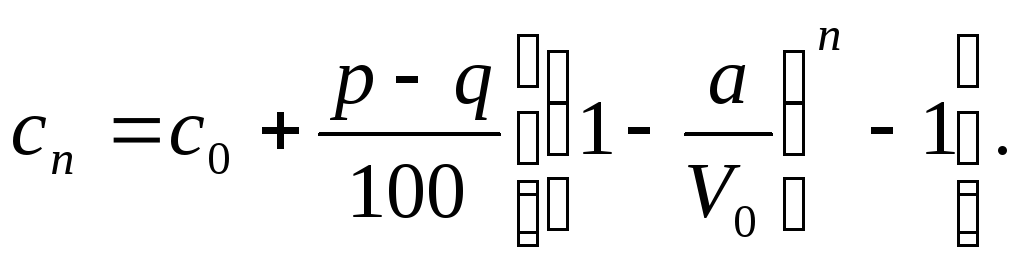
При додаванні правих частин розглянутих рівностей використовувалася формула для суми членів геометричної прогресії.
Підставляючи
замість
![]() її значення
її значення
![]() отримаємо формулу (3). Відмітимо, що при
отримаємо формулу (3). Відмітимо, що при
![]() ця формула переходить у раніше отриману
формулу (2).
ця формула переходить у раніше отриману
формулу (2).
Формула (2) тісно пов’язана з відомим у теорії відсотків правилом нарахування «складних відсотків».
2. Маємо два розчини однієї і тієї ж солі у воді. Для одержання суміші, що містить 10 г солі і 90 г води, беруть першого розчину вдвічі більше по масі, чим другого. Через тиждень з кожного кілограма першого і другого розчину випарувалося по 200 г води, і для одержання такої ж суміші, як і раніше, потрібно першого розчину уже вчетверо більше по масі, чим другого. Скільки грамів солі містилося спочатку в 100 г кожного розчину?
Відповідь. 5 г і 20 г.
3. Маємо три суміші, складені з трьох елементів А, В і С. У першу суміш входять лише елементи А і В у ваговому відношенні 3:5, у другу суміш входять лише елементи В і С у ваговому відношенні 1:2, у третю суміш входять лише елементи А і С у ваговому відношенні 2:3. У якому відношенні потрібно взяти ці суміші, щоб у знову отриманій суміші елементи А, В і С містилися у ваговому відношенні 3:5:2?
Відповідь. 20:6:3.
Задача. Маються два різних сплави міді зі свинцем. Якщо взяти 1 кг першого сплаву і 1 кг другого сплаву і переплавити їх, то вийде сплав, що містить 65 % міді. Відомо, що якщо взяти два шматки — шматок I і шматок II першого і другого сплавів відповідно, що мають сумарну масу 1 кг, і переплавити їх, то вийде сплав із вмістом 60% міді. Яка маса міді, що міститься в сплаві, що виходить при спільному переплавлянні шматка першого сплаву, рівного по масі шматку II, і шматка другого сплаву, рівного по масі шматку I?
Розв’язок. Уведемо процентні вмісти міді в сплавах: р% — в першому (концентрація міді р/100) і q% — в другому (концентрація міді q/100), а також масу шматка І — х кг і масу шматка ІІ — у кг. Складемо рівняння задачі.
|
Умова задачі |
Рівняння |
|
1 кг першого сплаву, переплавлений з 1 кг другого сплаву, дає сплав, що містить 65% міді |
|
|
Сумарна маса шматка I і шматка II дорівнює 7 кг |
|
|
Якщо переплавити шматок I і шматок II, то вийде сплав, що містить 60% міді |
|
Таким чином, виходить система трьох рівнянь з чотирма невідомими:
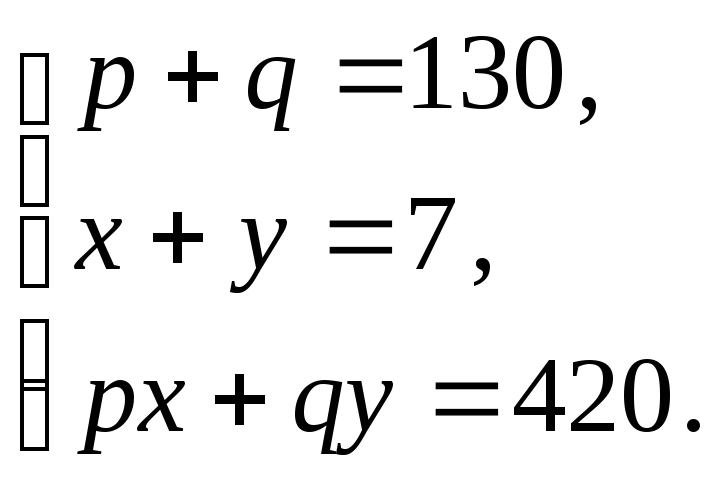
Звичайно, усієї чотири невідомих з такої системи однозначно знайти не можна. Тому звернемося до питання, на яке потрібно відповісти. Потрібно визначити, яка маса міді, що міститься в сплаві, що виходить при спільному переплавлянні шматка першого сплаву, рівного по масі шматку II, і шматка другого сплаву, рівного по масі шматку I, тобто величину
![]()
Система рівнянь цієї задачі має таку структуру, що величину qx + py можна легко знайти. Дійсно, перемножуючи почленно перше і друге рівняння і віднімаючи з добутку третє рівняння, одержуємо
![]()
Після цього знаходимо величину Q:
Q = 4,9 кг.
Відповідь. 4,9 кг.
5. Продають три шматки тканини. З першого продали половину, із другого 2/3, а третій шматок, у якому було 1/3 усієї тканини, продали весь. Скільки відсотків тканини продано, якщо всього залишилось її вдвічі менше, ніж було в другому шматку?
Відповідь. 75 %.
6. У лабораторії є розчини солі чотирьох різних концентрацій. Якщо змішати перший, другий і третій розчини у ваговому відношенні 3:2:1, то вийде 15%-й розчин. Другий, третій і четвертий розчини, узяті в рівній пропорції, дають при змішанні 24%-й розчин, і, нарешті, розчин, складений з рівних вагових частин першого і третього розчинів, має концентрацію 10%. Яка концентрація вийде при змішанні другого і четвертого розчинів у пропорції 2:1?
Відповідь. 0,29.
Задача. У 7 год. ранку з пункту А в пункт В за течією ріки відправляються байдарка і катер. Байдарка припливає в пункт В о 17 год того ж дня. Катер же, дійшовши до пункту В, миттєво повертає назад і на своєму шляху з В до А зустрічає байдарку не пізніше 15 год, а прибуває в пункт А не раніше 23 год. того ж дня. Знайти час прибуття катера в пункт В, якщо відомо, що власна швидкість катера в два рази більша власної швидкості байдарки.
Розв’язок. Своєрідність цієї задачі, як і попередньої, полягає в тому, що складених рівнянь недостатньо для однозначного визначення всіх невідомих. Це допомагають зробити наявні в задачі умови, що виражаються у вигляді нерівностей.
Нехай
![]() і
і
![]() — швидкості катера, байдарки (у стоячій
воді) і ріки відповідно,
— швидкості катера, байдарки (у стоячій
воді) і ріки відповідно,
![]()
![]() — відстань між пунктами А
і
В.
Тоді
маємо наступну таблицю:
— відстань між пунктами А
і
В.
Тоді
маємо наступну таблицю:
|
Умови задачі |
Рівняння або нерівність |
|
Байдарка знаходилася в дорозі 10 год |
|
|
На зворотному шляху з В в Л катер зустрів байдарку не пізніше 15 ч того ж дня |
|
|
Катер прибув назад у пункт А не раніше 23 ч того ж дня |
|
|
Катер може рухатися проти течії |
|
Пояснимо,
як була складена нерівність (2) системи.
Нехай
![]() — час (у годинах), що пройшов з початку
руху до зустрічі катера і байдарки. Тоді
— час (у годинах), що пройшов з початку
руху до зустрічі катера і байдарки. Тоді
![]()
Тут
![]() — час руху катера вниз по річці з А
до
В. Знайшовши
час t
з
отриманого рівняння, ми приходимо до
лівої частини нерівності (2).
— час руху катера вниз по річці з А
до
В. Знайшовши
час t
з
отриманого рівняння, ми приходимо до
лівої частини нерівності (2).
Знайдемо розв’язок системи нерівностей (1)—(4). Розділивши чисельник і знаменник кожного з дробів у лівій частині (2) і (3) на vб + u і з огляду на рівність (1), одержуємо
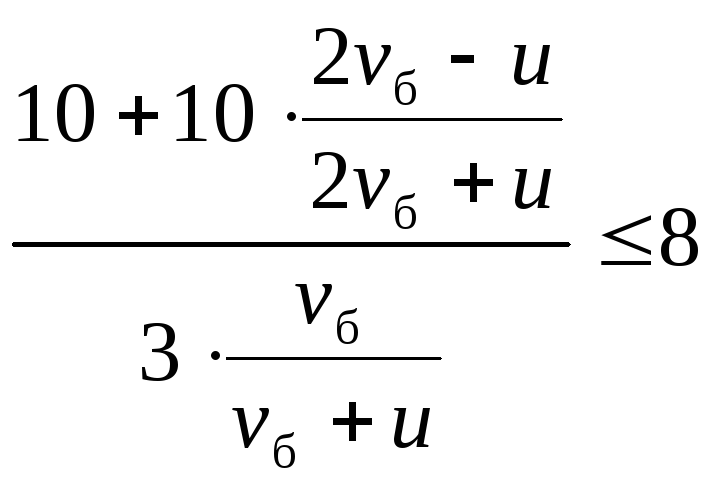 (2)
(2)
і
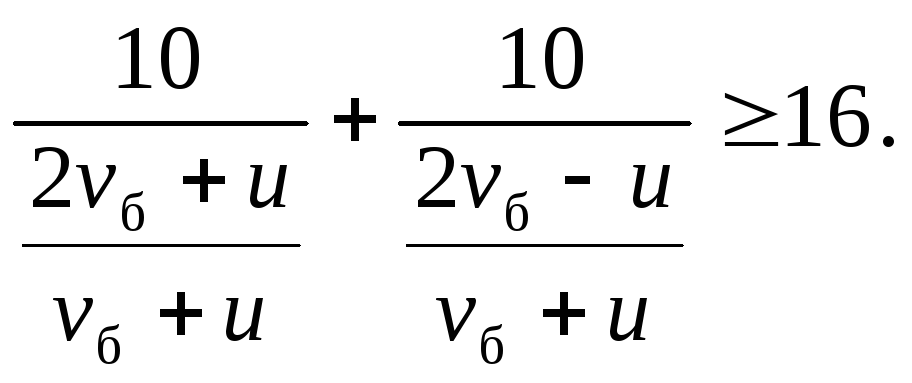 (3)
(3)
Отримані нерівності можна подати у такій формі:
![]()

або
![]() і
і
![]()
Звідси
видно, що ця система нерівностей
несуперечлива, якщо
![]() тобто
тобто
![]() .
Тоді з рівняння (1) одержуємо
.
Тоді з рівняння (1) одержуємо
![]() тобто
тобто
![]()
У задачі потрібно знайти час прибуття катера до пункт В. Знаходимо
![]()
Відповідь. Катер припливає в пункт В о 13 годині.
Один із прикладів задач такого типу нам уже зустрічався наприкінці попереднього параграфа. Розглянемо ще кілька прикладів.
Задача. З міста А в місті В відправився мандрівник, що у перший день пройшов 1/m-ю частину всього шляху. У наступний день він пройшов 1/m частину шляху, що залишився. У наступні дні він проходить поперемінно то 1/m частину, то 1/m частину шляху, що залишався до кінця попереднього дня. Через 10 днів такого руху з’ясувалося, що він пройшов 31/32 усієї відстані між містами А і В. Знайти m і n, якщо відомо, що m > n; m, n — цілі числа.
Розв’язок.
До
кінця першого дня відстань
![]() що відділяє мандрівника від міста В,
дорівнює
що відділяє мандрівника від міста В,
дорівнює
![]() ,
,
де s — відстань між містами.
До кінця другого дня відстань s2, що відокремлює його від міста В, стає рівною
![]()
![]()
Повторюючи
ці міркування (див. формулу складних
відсотків у § 1), одержуємо, що до кінця
10-го дня шляху до міста В
залишилося
пройти відстань
![]() що дорівнює
що дорівнює
![]()
Тому єдине рівняння в цій задачі має вигляд
![]() (1)
(1)
Вилучаючи корінь п’ятого ступеня з обох його частин, одержуємо
![]()
або
![]() (2)
(2)
Таким
чином, потрібно знайти єдиний розв’язок
одного рівняння з двома невідомими.
Виявляється, що це можна зробити, але
тільки враховуючи, що т
і
п
—
цілі позитивні числа
![]()
Виражаючи, наприклад, т з останнього рівняння, одержуємо
![]()
і оскільки
![]() не задовольняє цьому рівнянню, знаходимо
не задовольняє цьому рівнянню, знаходимо
![]()
Беручи
до уваги, що т
— ціле
число, заключаємо, що і дріб
![]() також повинна бути цілим числом. З огляду
на, що
також повинна бути цілим числом. З огляду
на, що
![]() і
і
![]() неважко побачити, що розглянуте відношення
набуває цілих значень тільки при
неважко побачити, що розглянуте відношення
набуває цілих значень тільки при
![]() і
і
![]() Якщо
Якщо
![]() ,
то
,
то
![]() Якщо
Якщо
![]() то
то
![]() Враховуючи умову задачі:
Враховуючи умову задачі:
![]() одержуємо єдиний розв’язок:
одержуємо єдиний розв’язок:
![]()
![]()
Отже, розв’язок знайдено.
Розглянемо ще один приклад.
1. Хтось придбав 30 птахів за 30 монет. З числа цих птахів за кожних трьох горобців заплачена 1 монета, за кожних двох горлиць — також 1 монета, за кожного голуба — 2 монети. Скільки було куплено птахів кожної породи?
Відповідь. 9 горобців, 10 горлиць, 11 голубів.
10. У школяра була деяка сума грошей монетами достоїнством у 15 коп. і 20 коп., причому 20-копійчаних монет було більше, ніж 15-копійчаних. П’яту частину всіх грошей школяр витратив, віддавши дві монети на квиток у кіно. Половину грошей, що залишилися в нього, він віддав за обід, оплативши його трьома монетами. Скільки монет кожного достоїнства було в школяра спочатку?
Відповідь. 2 п’ятнадцятикопійчані монети і 6 двадцятикопійчані монети.
Задача.
Автомобіль
виїжджає з пункту А
і їде з постійною швидкістю
![]() км/год. до пункту В,
що відстоїть від пункту А
на відстані 24,5 км. У пункті В
автомобіль переходить на рівноуповільнений
рух, причому за кожну годину його
швидкість зменшується на 54 км/год., і
рухається так до повної зупинки. Потім
автомобіль відразу ж повертає назад і
повертається в А
з постійною швидкістю
км/год. до пункту В,
що відстоїть від пункту А
на відстані 24,5 км. У пункті В
автомобіль переходить на рівноуповільнений
рух, причому за кожну годину його
швидкість зменшується на 54 км/год., і
рухається так до повної зупинки. Потім
автомобіль відразу ж повертає назад і
повертається в А
з постійною швидкістю
![]() .
Якою повинна бути швидкість
.
Якою повинна бути швидкість
![]() ,
щоб автомобіль за найменший час проїхав
шлях від А
до повної зупинки і назад до пункту А
зазначеним вище способом?
,
щоб автомобіль за найменший час проїхав
шлях від А
до повної зупинки і назад до пункту А
зазначеним вище способом?
Розв’язок.
Підрахуємо
час, що затрачає автомобіль на весь шлях
від А
до
повної зупинки і назад. Покажемо, що цей
час визначається одним невідомим
параметром
![]() .
.
1. Відстань 24,5 км автомобіль проїжджає за час
![]()
2. Слідом за цим він рухався до повної зупинки з прискоренням — 54 км/год2 протягом часу
![]()
пройшовши при цьому відстань s, що визначається за відомою формулою для рівноприскореного руху:
![]()
![]()
3. Час, витрачений на зворотній шлях, дорівнює
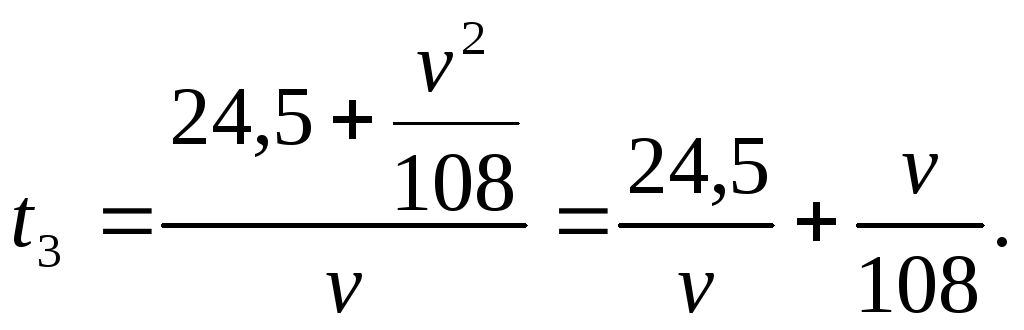
Тому повний час руху автомобіля
![]()
Таким
чином, час руху автомобіля від пункту
А
до
повної зупинки і назад є функцією однієї
перемінної
![]() — його швидкості на першій ділянці:
— його швидкості на першій ділянці:
![]()
Визначимо
тепер, при якому значенні
![]() ця функція досягає свого мінімуму. Для
цього обчислимо її похідну
ця функція досягає свого мінімуму. Для
цього обчислимо її похідну
![]()
![]()
Необхідною умовою екстремуму диференційованої функції є рівність нулю її похідної
![]()
![]()
Звідси
знаходимо, що
![]() При цьому значенні змінної функція
При цьому значенні змінної функція
![]() має
мінімум, оскільки
має
мінімум, оскільки
![]() при
при
![]() і
і
![]() при
при
![]() Таким чином, при швидкості 42 км/год.
автомобіль, рухаючись зазначеним вище
способом, витратить на весь шлях
мінімально можливий час.
Таким чином, при швидкості 42 км/год.
автомобіль, рухаючись зазначеним вище
способом, витратить на весь шлях
мінімально можливий час.

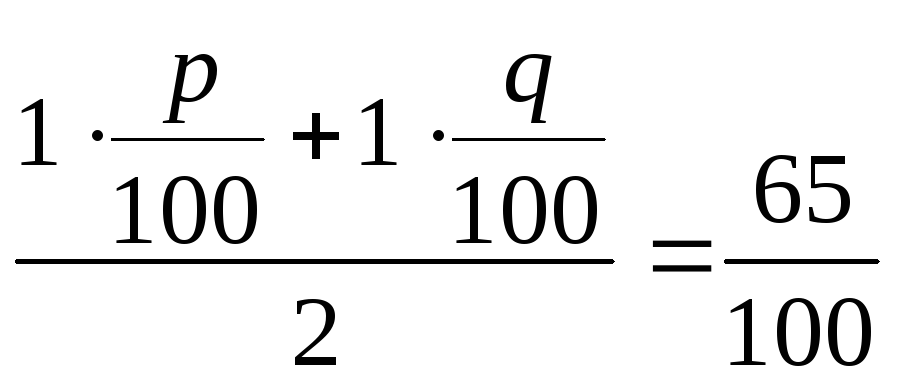
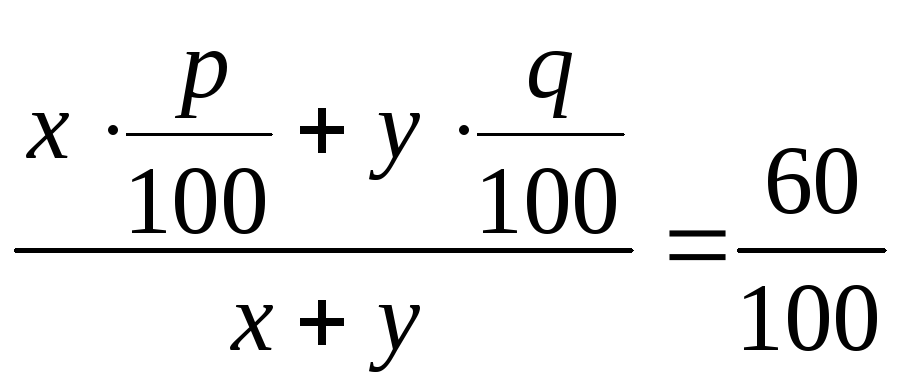
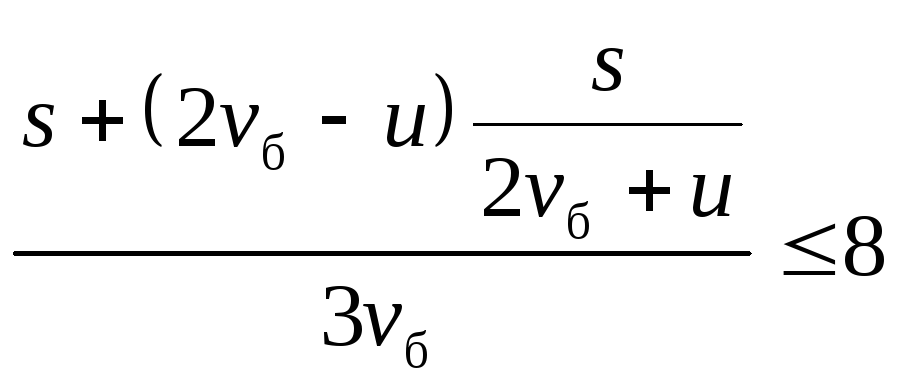 (2)
(2)