7.5. Графік і властивості функції
Функція
безупинна і монотонні на проміжку
.
Зворотна до неї функція
називається арккотангенсом (мал. 7.5).
Рис. 7.5.
Функція
монотонно убуває і задовольняє нерівності
(18)
Виконано граничні співвідношення
. (19)
Визначення.
Арксотангенсом
називається кут
,
що задовольняє нерівності (18), котангенс
якого дорівнює
,
тобто
,
. (20)
З графіків (7.4), (7.5) видно, що завжди виконано рівності
, (21)
. (22)
Приведемо табличні значення арккотангенса:
,
,
,
,
. (23)
а також формули для тригонометричних функцій
,
,
,
,
,
,
,
,
.
(24)
Приклад. Обчислимо значення функції
.
Приклад. Обчислимо значення функції
.
Приведемо більш складні приклади обчислення значень зворотних тригонометричних функцій. Знайдемо вираження для суми
,
,
,
.
Остаточно знаходимо формулу
.
Приклад.
.
Приклад.
.
Значення
вибирається у формулі, якщо відомо
наближене значення
.
Обчислити:
,
,
.
Обчислити:
.
Позначимо
,
,
,
.
Обчислити:
.
Знаходимо по формулі для суми арктангенсів
;
;
.
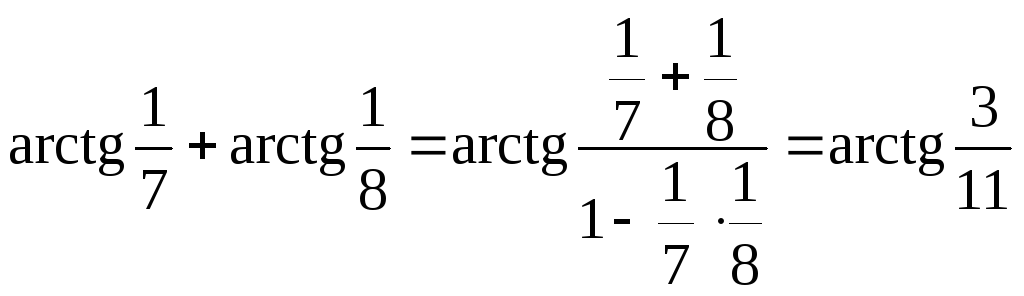Обчислити:
.
Позначимо
,
;
.
7.6. Рівняння зі зворотними тригонометричними функціями
До рівнянь зі зворотними тригонометричними функціями застосовують тригонометричні функції.
Приклад.
.
Запишемо
,
,
.
Варто
перевірити корені рівняння
,
числа
теж є коренями вихідного рівняння.
Приклад
.
Позначимо
і вирішуємо рівняння
.
Застосуємо функцію
до обох частин рівняння
,
,
,
.
Друге
рішення
не задовольняє рівнянню.
,
.
Приклад.
.
,
,
,
,
,
,
.
рівняння
не має рішення;
,
,
.
Рішення
не задовольняє рівнянню, так
,
.
.
Приклад.
.
Використовуємо тотожність
;
,
;
;
,
,
,
,
,
.
Приклад.
,
,
,
,
,
.
Рішення
не задовольняє вихідному рівнянню.
Приклад.
,
,
,
,
;
,
.
Приклад.
,
,
,
.
Приклад.
,
,
,
,
.
Приклад.
.
,
,
,
;
.
7.7. Основні найпростіші тригонометричні рівняння
Зворотні тригонометричні функції використовуються для рішення тригонометричних рівнянь. Приведемо найпростіші способи рішення тригонометричних рівнянь.
1.
Рівняння
,
має рішення, які можна визначити формулою
,
(26)
Рішення можна пояснити на мал. 7.6
Рис. 7.6.
За
традицією невідомий кут позначається
буквою
.
У межах
рівняння
має рішення
.
У межах
є інше, симетричне щодо осі
рішення
.
При
ці симетричні рішення збігаються. Щоб
не було повторення рішень при
рішення визначають по інших формулах
,
,
,
,
,
.
При
рішення рівняння
можна записати у виді (26)
,
чи в рівносильній формі
,
.
До
рішень завжди варто додавати доданок
,
,
що не змінює значення
.
При
рівняння
не має дійсних рішень.
Приклад.
Знайдемо рішення рівняння
.
По формулі (26) знаходимо
,
,
.
Приклад.
Вирішимо рівняння
.
Оскільки
,
те одержимо
,
,
.
2.
Рівняння
,
має рішення
,
(27)
Рішення
можна пояснити на мал. 7.7. Кути, обумовлені
рішенням розташовані симетрично щодо
осі
Рис. 7.7.
Рівняння
мають рішення
,
,
,
,
,
.
Приклад.
Знайдемо рішення рівняння
.
По формулі (27) одержимо:
,
,
,
.
Приклад.
,
,
,
.
3.
Рівняння
має рішення
,
.
(28)
Ці рішення можна представити на мал. 7.8.
Рис. 7.7.
Приклад.
Вирішимо рівняння
.
По формулі (28) знаходимо
,
,
.
Приклад.
Вирішимо рівняння
.
Представимо рівняння у виді:
,
,
,
.