Тема 7. Зворотні тригонометричні функції. Тригонометричні рівняння.

7.1. Зворотна функція.

7.2. Графік і властивості функції .

7.3. Графік і властивості функції .

7.4. Графік і властивості функції .

7.5. Графік і властивості функції .

7.6. Рівняння зі зворотними тригонометричними функціями.

7.7. Основні найпростіші тригонометричні рівняння.

7.8. Лінійне рівняння.

7.9. Зведення тригонометричного рівняння до алгебраїчного.

7.10. Розкладання рівняння на множники.

7.11. Рівність однойменних функцій.

7.12. Перетворення добутків у суми, а сум у добуток.

7.13. Рішення, засновані на обмеженості функцій.

7.14. Системи тригонометричних рівнянь.

Питання для самоперевірки.

Вправи для самостійного розв’язування.

7.1. Зворотна функція

Нехай функція безупинна і монотонна на інтерваліі при цьому перемінназмінюється на інтервалі. Розв'язно рівняннявідносноі знайдемо рішення. Функціяназивається зворотної до функції. При зазначених умовах зворотна функціяіснує і безупинна при. При цьому справедливі рівності

, ;

, (1)

Графіки функцій ,розташовані симетрично щодо бісектриси першого координатного кута.

Приклад. Функція ,визначає залежність між перемінними, котру також можна задати рівнянням,. У прикладі,. Рівності (1) приймуть вид

, ;

, .

Графіки функцій ,розташовані симетрично щодо бісектриси першого координатного кута (Рис. 7.1).

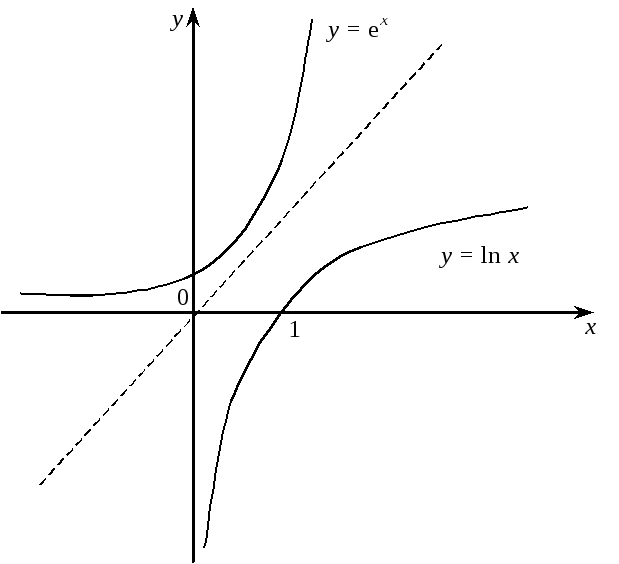
Рис. 7.1.

7.2. Графік і властивості функції .

Функція монотонна при. Зворотна до неї функція,називається арксинусом (мал. 7.2).

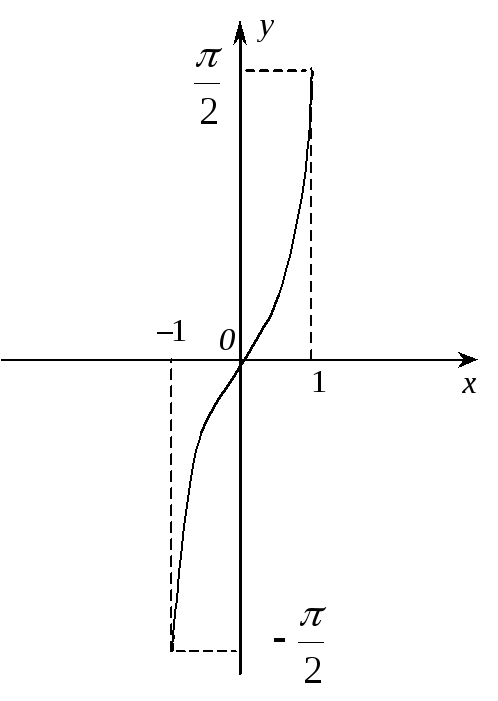
Рис. 7.2.

Функція монотонно зростає на відрізкуі задовольняє нерівності

(2)

Визначення. Арксинусом називається кут, що задовольняє нерівності (2), синус якого дорівнює.

, . (3)

Приведемо деякі числові значення , що задовольняє нерівності (2), синус якого дорівнює.

, ,,

, . (4)

Функція — непарна, тобто

. (5)

Приведемо деякі формули

, ,

, ,

, ,

, ,.

Приклад. Обчислити . Одержимо.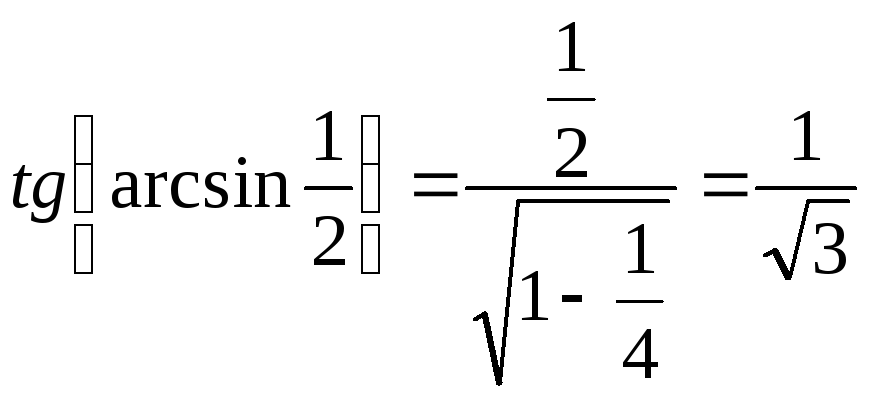

Приклад. Вирішити нерівність . Маємо:;. Оскільки є обмеження, то одержимо відповідь:.

7.3. Графік і властивості функції .

Функція монотонна при. Зворотна до неї функція,називається арккосинусом (Рис. 7.3)

Рис. 7.3.

Функція монотонно убуває на відрізкуі задовольняє нерівності

(6)

Визначення. Арккосинусом називається кут, що задовольняє нерівності (6), косинус якого дорівнює, тобто

, . (7)

У силу симетрії графіка щодо крапки виконана рівність

,

відкіля знаходимо формулу

. (8)

З порівняння графіків ,знаходимо рівність

, . (9)

Приведемо деякі числові значення .

, ,,

, (10)

Приведемо формули:

; ;

; ;

, ,

, . (11)

Приклад. Обчислити значення функції

.

Приклад. Обчислити значення функції

.

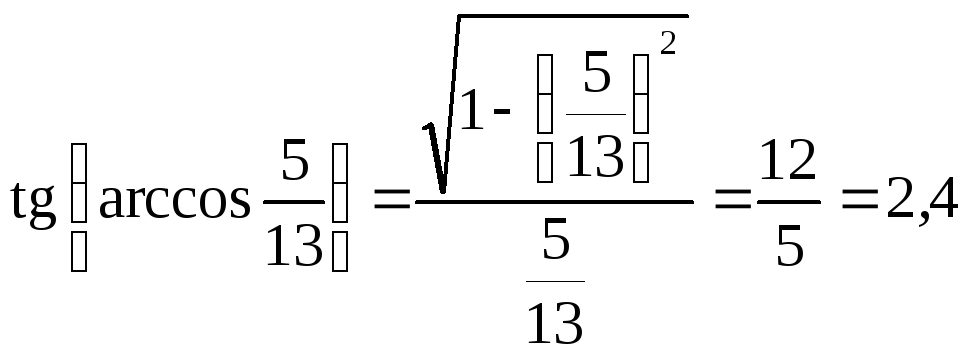7.4. Графік і властивості функції

Функція монотонна при. Зворотна до неї функція,називається арктангенсом (Рис. 7.4)

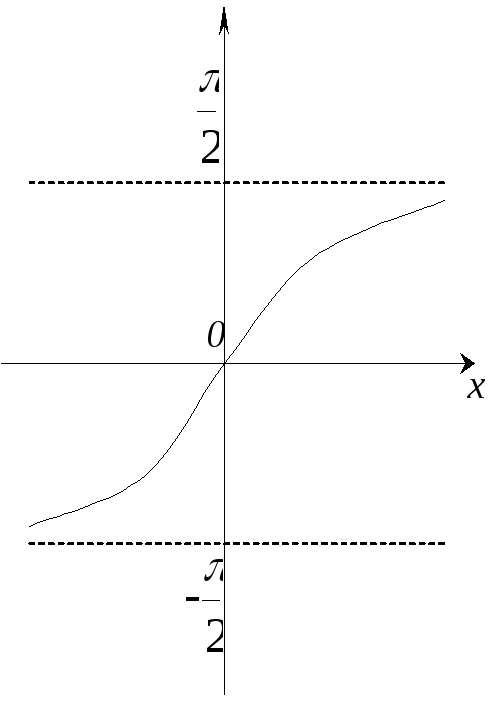
Рис. 7.4.

Функція монотонно зростає, непарна і задовольняє нерівності

. (12)

Виконано граничні співвідношення

, . (13)

Визначення. Арктангенсом називається кут, що задовольняє нерівності (12), тангенс якого дорівнює, тобто

, . (14)

Функція приймає наступні значення:

, ,;

, . (15)

Приведемо деякі формули:

; ,

; ,

; ,

; ,. (16)

Приклад. Обчислити значення:

.

Приклад. Обчислити значення суми

.

Виведемо формулу для суми арктангенсів.

Нехай справедлива рівність .

Знаходимо значення

.

Звідси знаходимо формулу

. (17)

Оскільки виконані нерівності (12), те число K може приймати значення ,.

Приклад. Знайде значення суми

.

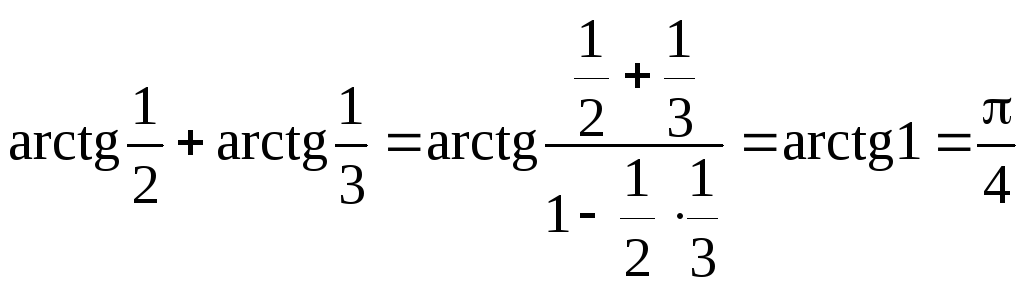Приклад. Знайдемо значення суми

.