
- •3.1. Властивості ступенів і коренів
- •Підкореневий вираз розкладемо на прості множники:
- •3.2. Дії з радикалами
- •3.3. Обчислення ірраціональних виразів
- •3.4. Оцінки для радикалів
- •Відповідь
- •4.1. Загальні відомості про рівняння
- •4.2. Рівняння першого степеня з одним невідомим
- •Відповідь
- •4.3. Рівняння другого степеня з одним невідомим
- •4.4. Задачі на використання властивостей дискримінанта
- •4.5. Використання формул Вієта
- •4.6. Розміщення коренів квадратного рівняння
- •Відповіді
- •4.7. Алгебраїчні рівняння вищих степенів та їхні властивості
- •Застосування теореми Гаусса
- •4.9. Рівняння, що зводяться до квадратних рівнянь
- •2. Рівняння вигляду
- •3. Рівняння виду
- •4. Рівняння вигляду
- •Зворотні (симетричні) рівняння
- •Однорідні рівняння
- •4.10. Метод Кардано для розв’язання кубічного рівняння
- •4.11. Уведення параметра замість сталого коефіцієнта
4.5. Використання формул Вієта
Приклад.
Знайти значення параметра
![]() ,
при яких відношення коренів рівняння
,
при яких відношення коренів рівняння
![]()
дорівнює 2.
Маємо систему рівнянь
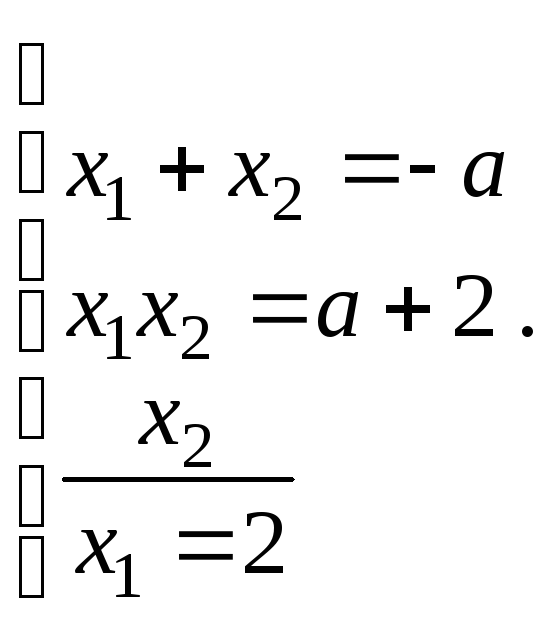
Оскільки
шукаємо тільки значення параметра
![]() ,
то виключаємо невідомі
,
то виключаємо невідомі
![]() .
Маємо рівняння:
.
Маємо рівняння:
![]() .
.
Останнє
рівняння має розв’язки
![]() ,
,
![]() .
.
При
![]() маємо
маємо
![]() ,
,
![]() ,
а при
,
а при
![]()
![]() ,
,
![]() .
.
Приклад.
Знайти добуток значень параметра
![]() ,
при яких сума коренів рівняння
,
при яких сума коренів рівняння
![]()
дорівнює сумі їхніх квадратів.
Скориставшись формулами Вієта, дістанемо систему
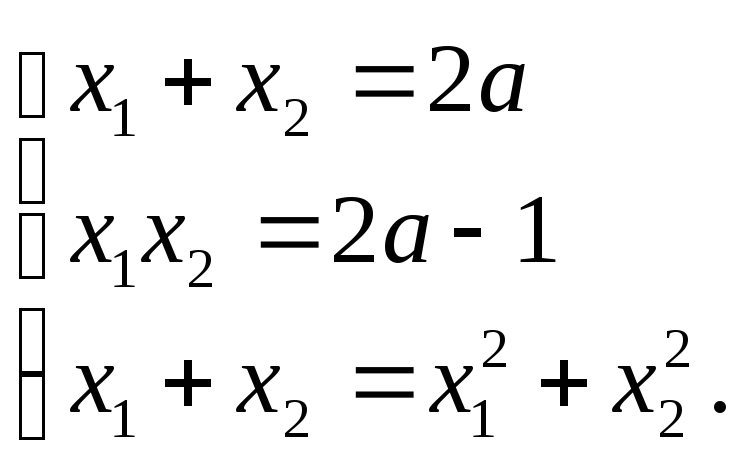
Останнє рівняння можна записати у вигляді
![]() .
.
Виключаючи
![]() ,
дістаємо рівняння для
,
дістаємо рівняння для
![]()
![]() .
.
Приклад.
Знайти ціле значення параметра
![]() ,
при якому рівняння
,
при якому рівняння
![]()
має рівні між собою корені.
Квадратне рівняння має рівні між собою корені, якщо його дискримінант дорівнює нулю. Розв’яжемо рівняння
![]() ,
,
звідки
![]() ,
,
![]() .
Значення
.
Значення
![]() шукане.
шукане.
Приклад. Знайти суму кубів коренів рівняння
![]() .
.
Можна знайти корені рівняння
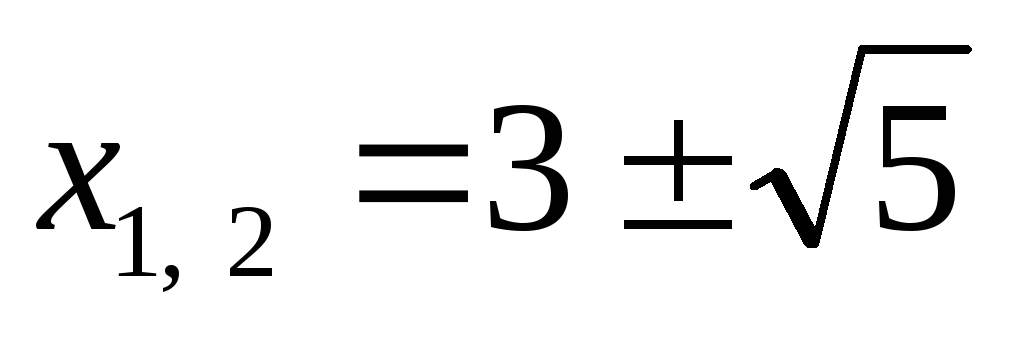 і обчислити суму кубів коренів:
і обчислити суму кубів коренів:
![]() .
.
Таку саму відповідь можна дістати за допомогою формул Вієта:
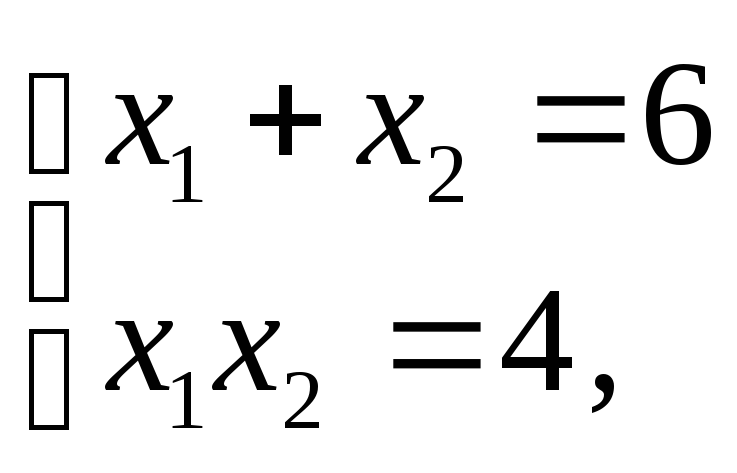
![]()
Функція
![]() називається симетричною, якщо вона не
змінюється внаслідок довільного
перестановлення аргументів, тобто
називається симетричною, якщо вона не
змінюється внаслідок довільного
перестановлення аргументів, тобто
![]() .
.
Коефіцієнти зведеного квадратного рівняння
![]()
є симетричними функціями від коренів рівняння.
Довільну
симетричну функцію
![]() завжди можна подати через основні
симетричні функції
завжди можна подати через основні
симетричні функції
![]() ,
,
![]() .
Це й було виконано в попередньому
прикладі.
.
Це й було виконано в попередньому
прикладі.
Приклад.
При яких значеннях параметра
![]() сума квадратів коренів рівняння
сума квадратів коренів рівняння
![]()
буде мінімальною?
Використовуючи формули Вієта, дістаємо:
![]() .
.
Знаходимо дискримінант рівняння
![]() .
.
Оскільки
при довільних значеннях параметра
![]() виконується нерівність
виконується нерівність
![]() ,
то на значення параметра
,
то на значення параметра
![]() обмежень немає. Сума квадратів коренів
набуває найменшого значення, що дорівнює
1, при
обмежень немає. Сума квадратів коренів
набуває найменшого значення, що дорівнює
1, при
![]() .
.
Приклад.
При якому значенні параметра
![]() сума квадратів коренів рівняння
сума квадратів коренів рівняння
![]()
набуває найменшого значення?
Знаходимо дискримінант рівняння (1):
![]() .
.
З
умови
![]() знаходимо, що рівняння (1) має розв’язок
лише при
знаходимо, що рівняння (1) має розв’язок
лише при
![]() .
Знаходимо суму квадратів коренів
рівняння (1) за формулами Вієта:
.
Знаходимо суму квадратів коренів
рівняння (1) за формулами Вієта:
![]() .
.
Найменшого
значення лінійна функція
![]() може набувати лише на кінці відрізка
може набувати лише на кінці відрізка
![]() .
.
Оскільки
![]() ,
то
,
то
![]() досягається при
досягається при
![]() .
.
Приклад.
При яких значеннях параметра
![]() рівняння
рівняння
![]() ,
,
![]()
мають спільний корінь?
Запишемо рівняння Вієта
![]() ,
,
а
далі візьмемо
![]() .
Крім значень
.
Крім значень
![]() дістаємо також
дістаємо також
![]() .
Рівняння
.
Рівняння
![]() ,
,
![]()
мають
спільний корінь
![]() .
.
Ще один спосіб розв’язування прикладу полягає ось у чому.
Нехай
![]() — шуканий спільний корінь рівнянь.
Маємо систему алгебраїчних рівнянь
— шуканий спільний корінь рівнянь.
Маємо систему алгебраїчних рівнянь
 (2)
(2)
Виключимо
![]() ,
помноживши друге рівняння на
,
помноживши друге рівняння на
![]() і віднявши від першого рівняння. Дістанемо
рівняння
і віднявши від першого рівняння. Дістанемо
рівняння
![]() .
.
При
![]() рівняння (2) не мають дійсних розв’язків.
рівняння (2) не мають дійсних розв’язків.
Виключаючи
![]() ,
дістаємо рівняння для параметра
,
дістаємо рівняння для параметра
![]() :
:
![]() ,
,
![]() .
.
При
![]() рівняння (2) не мають спільного кореня.
При
рівняння (2) не мають спільного кореня.
При
![]() рівняння (2) мають спільний корінь
рівняння (2) мають спільний корінь
![]() .
.
Приклад.
Знайти значення параметра
![]() ,
при якому один із коренів рівняння
,
при якому один із коренів рівняння
![]() (3)
(3)
утричі менший від одного з корнів рівняння
![]() . (4)
. (4)
Нехай
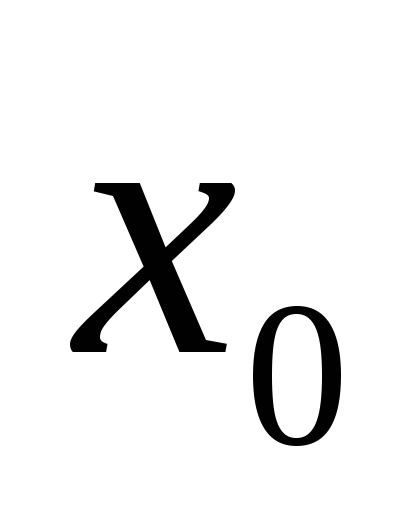 — корінь рівняння (3),
— корінь рівняння (3),
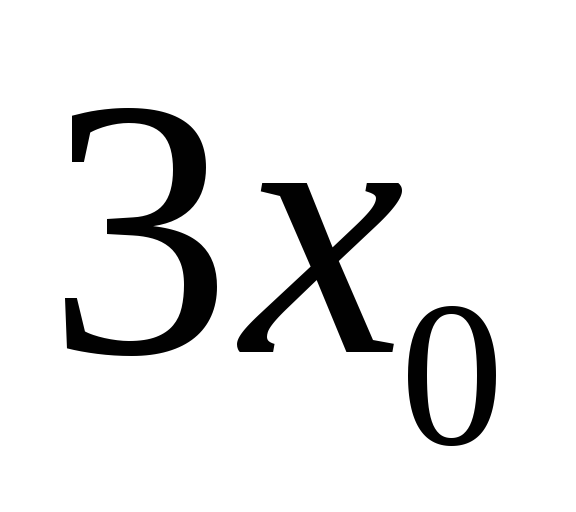 — корінь рівняння (4). Маємо систему
рівнянь
— корінь рівняння (4). Маємо систему
рівнянь
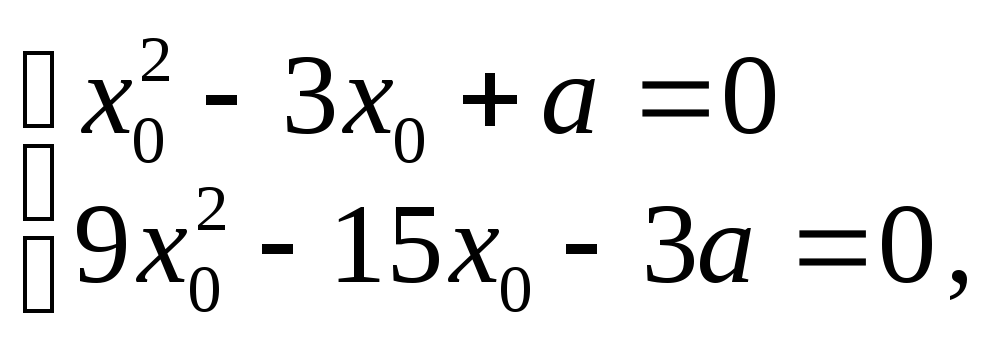
з
якої знаходимо
![]() .
Підставляючи
.
Підставляючи
![]() в рівняння (3), дістаємо
рівняння для
в рівняння (3), дістаємо
рівняння для
![]() :
:
![]() .
.
При
![]() рівняння (3) має корінь
рівняння (3) має корінь
![]() ,
а рівняння (4) — корінь
,
а рівняння (4) — корінь
![]() .
.
При
![]() рівняння (3) має корінь
рівняння (3) має корінь
![]() ,
а рівняння (4) — корінь
,
а рівняння (4) — корінь
![]() .
.
