elem_mat / R_8
.docТема 8. Показові логарифмічні рівняння
8.1. Показова функція
8.2. Логарифмічна функція
8.3. Перетворення логарифмічних виразів
8.4. Способи розв’язання логарифмічних рівнянь
8.5. Способи розв’язання показових рівнянь
8.6. Показово-степеневі рівняння
8.7. Системи показових і логарифмічних рівнянь
Питання для самоперевірки
Вправи для самостійного розв’язування
Тема 8. Показові логарифмічні рівняння
Для наближеного вичислення показової і логарифмічної функцій можна використати наступні розкладання
,
.
Збіжність можна отримати якщо покладемо
,
.
Показову функцію можна розкласти в ряд
.
Збіжність ряду можна покращити, поклавши
.
Значення логарифмів можна знайти з розкладання
,
.
Отримаємо
і отримаємо розкладання в ряд
Ці розкладання можна використовувати при комплексних значеннях аргументів. В подальшому припускаємо, що всі аргументи і функції є дійсними.
8.1. Показова функція
Приведемо
деякі властивості показників функції
.
1.
.
2.
.
3.
.
4.
.
5.
.
6.
.
7.
.
При
показова функція
зростає при всіх значеннях х,
при
показова функція убуває при всіх
значеннях х
(Рис. 8.1).
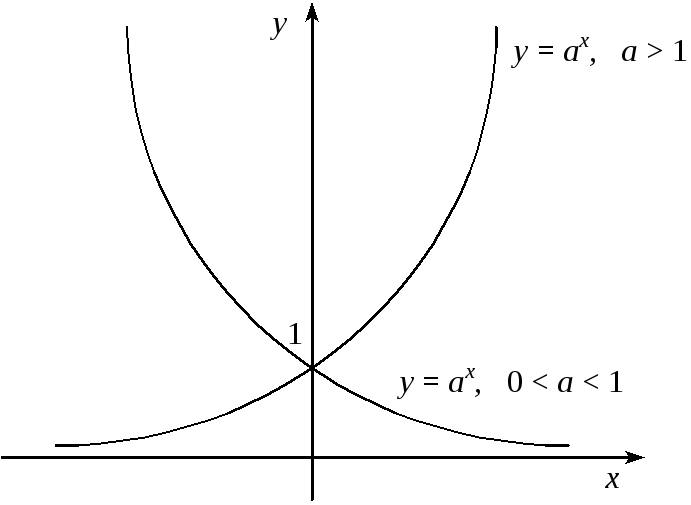
Рис. 8.1
8.2. Логарифмічна функція
Логарифмічна
функція
є функція зворотна до показової функції
.
При
логарифмічна функція зростає при
,
при
логарифмічна функція убуває при
(Рис. 8.2).
Рис. 8.2
Визначення. Логарифм числа b по заснуванню а називається степінь, в яку потрібно звести до основи а, щоб отримати число b
.
Звичайно
думають
.
Основні тотожності для визначення логарифмів
.
Приведемо деякі властивості логарифмів
1.
.
2.
.
3.
.
4.
.
5.
.
6.
.
7.
Формула переходу до нової основи
.
8.
.
9.
.
10.
11.
.
12.
.
Доказ останніх формул 8—11 випливає з формули 7.
8.3. Перетворення логарифмічних виразів
Обчислити
1.
.
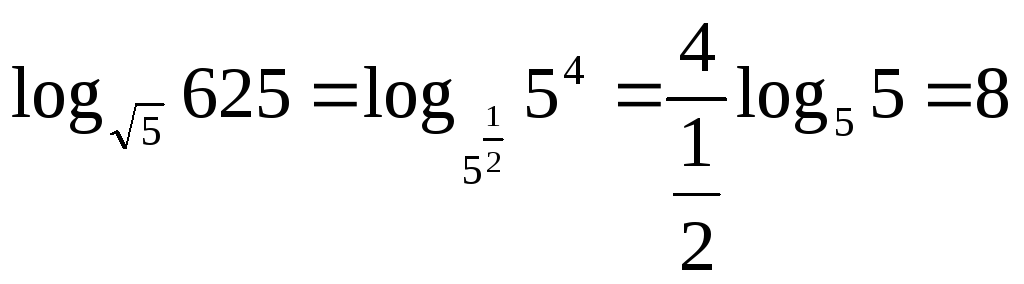2.
.
3.
.
4.
.
5.
.
6.
.
7.
.
Позначимо:
,
тоді
,
.
Отримаємо
.
8.
.
Покладемо
,
отримаємо
.
.
9.
.
10.
.
11.
.
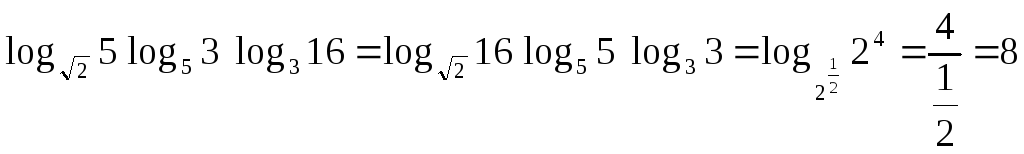12.
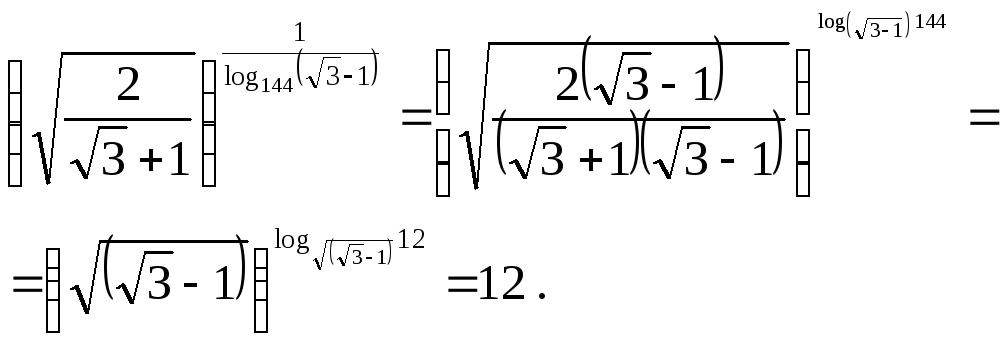
13.
Знайти
,
якщо
.
.
14.
Дано:
.
Знайти
.
.
15.
Знайти
,
якщо
.
Перейдемо до основи х.
.
.
8.4. Способи розв’язання логарифмічних рівнянь
1. Перехід до загальної основи. Якщо в рівнянні є логарифми з різними основами, то переходимо до загальної основи.
Приклад.
,
,
.
Приклад.
.
Переходимо до основи 5.
,
.
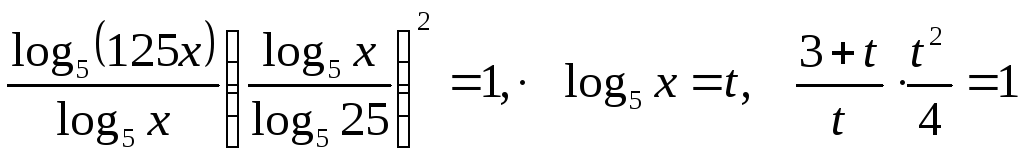2. Потенціювання. Якщо під знаком логарифма є сума або різниця, то рівняння потенціюють. Розв’язок обов’язково перевіряють.
Приклад.
.
Перейдемо до основи 2.
.
Потенціюємо
рівняння.
.
Корінь
не задовольняє рівняння.
Приклад.
.
Корінь
не задовольняє рівняння.
3. Логарифмування. Якщо в показнику при невідомому є логарифми невідомого, то звичайно рівняння логарифмується.
Приклад.
,
.
Логарифмуємо рівняння по основі 10.
.
Приклад.
,
,
,
.
4. Спосіб позначень. Логарифмічне рівняння зводиться до алгебраїчного рівняння.
Приклад.
,
,
.
Приклад.
.
Позначимо
.
.
5.
Розкладання на множники. Рівняння
розкладається на множники
і кожний множник прирівнюється до нуля.
Приклад.
,
,
.
Приклад.
.
Позначимо:
,
.
Отримаємо рівняння
,
які розкладаємо на множники.
,
.
1)
2)
.
Корінь
не задовольняє рівняння.
6.
Графічний спосіб розв’язання.
Рівняння записується у вигляді
.
Будуються графіки функцій
,
і шукаються точки їх перетинання, які
визначають розв’язок рівняння.
Приклад.
Розв’яжемо графічні рівняння
.
Графіки
функцій
,
перетинаються в точці
.
Розв’язок
.
Приклад. Розв’яжемо рівняння
.
Позначимо
.
Отримаємо
рівняння:
,
які мають очевидне розв’язання
.
Ліва частина монотонно зростає і тому
— єдиний корінь.
.
Звичайно при розв’язанні логарифмічних рівнянь використовується декілька способів їх перетворення.
Приклад.
.
Переходимо до основи 3.
.
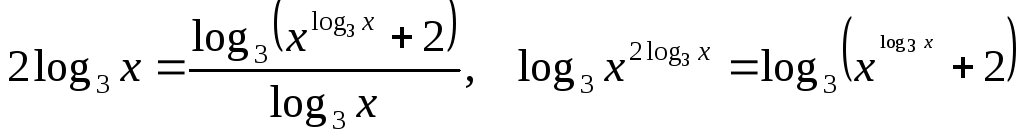Потенціюємо
рівняння:
:
.
Логарифмуємо рівняння по основі 3.
.
Приклад.
.
1. Припустимо,
що
.
Рівняння приймає вид тотожності
.
2. Нехай
.
Отримаємо рівняння
.
Потенціюємо рівняння.
.
8.5. Способи розв’язання показових рівнянь
1. Прирівнювання показників при одній підставі
З
рівняння
знаходимо
.
Приклад.
,
;
.
Приклад.
.
Прирівнюємо показники при основі 5.
.
Корінь
не задовольняє рівняння.
2. Логарифмування рівняння.
Приклад.
.
Логарифмуємо рівняння по основі 3.
,
.
Приклад.
.
Оскільки
,
то можна логарифмувати рівняння.
.
3. Спосіб позначень.
Приклад.
.
Позначимо
.
.
.
Приклад.
.
Позначимо
.
При цьому
;
.
.
Приклад.
.
Позначимо
:
.
4. Однорідні рівняння.
Рівняння
,
можна переписати у вигляді
.
Вважаючи
,
отримаємо рівняння
.
Приклад.
.
Перепишемо рівняння у вигляді
,
.
Приклад.
х = 1,18681439.
Приклад.
.
Запишемо рівняння у вигляді
;
.
5. Розкладання рівняння на множники.
Рівняння
намагаємося подати у вигляді
і прирівнюємо до нуля кожний множник.
Приклад.
.
Покладемо
і розкладемо рівняння
на множники
.
Приходимо до рівняння:
;
.
Рівняння розв’язується графічно і
знаходимо корінь
.
Приклад.
.
Покладемо
і згрупуємо члени з множниками
.
1)
,
2)
,
;
.
Корінь
не задовольняє рівняння.
8.6. Показово-степеневі рівняння
Розглядається рівняння
Приведемо часткові випадки цього рівняння.
1)
,
функція
існує.
2)
,
функції
існує.
3)
,
,
.
4)
.
Числа
— цілі, одинакові парності.
Приклад.
.
1)
.
2)
.
3)
.
При підстановці
в рівнянні отримаємо
.
Оскільки
— не існуюче вираження, то корінь
не задовольняє рівняння.
4.
.
Приклад.
.
1)
.
2)
.
3)
— не задовольняє рівняння.
4)
.
Деякі рівняння можна розглядати як показові так і логарифмічні.
Приклад.
.
Потенціюємо
рівняння.
,
.
Приклад.
Розв’яжемо рівняння
.
Переходимо до
основи 3.
;
.
1)
.
2)
.
Приклад.
:
.
8.7. Системи показових і логарифмічних рівнянь
Для розв’язання системи рівнянь намагаються зменшити число рівнянь, крім невідомих.
Приклад.
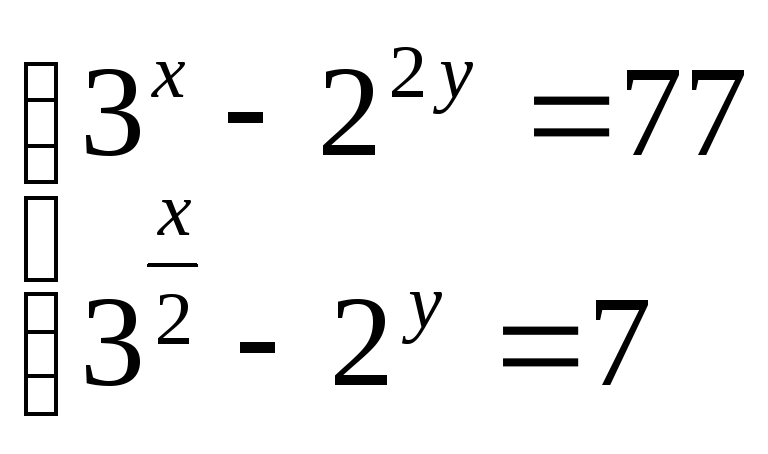
Позначимо
.
Отримаємо систему рівнянь
.
Приклад. Логарифмуємо систему рівнянь
по основі 2. Отримаємо систему лінійних рівнянь
.
З
очевидним розв’язком
.
Приклад.
.
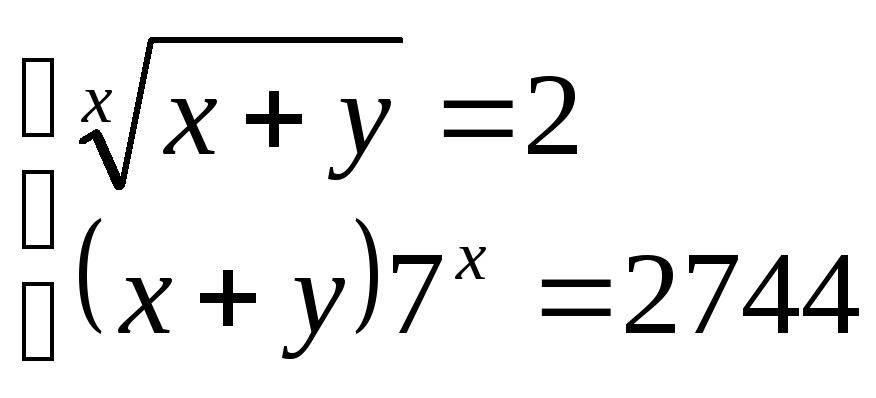Виключаємо
і приходимо до одного рівняння
.
Приклад.
.
Розділимо перші рівняння на другі
.
Приклад.
.
Запишемо систему рівнянь у вигляді
.
Приклад.
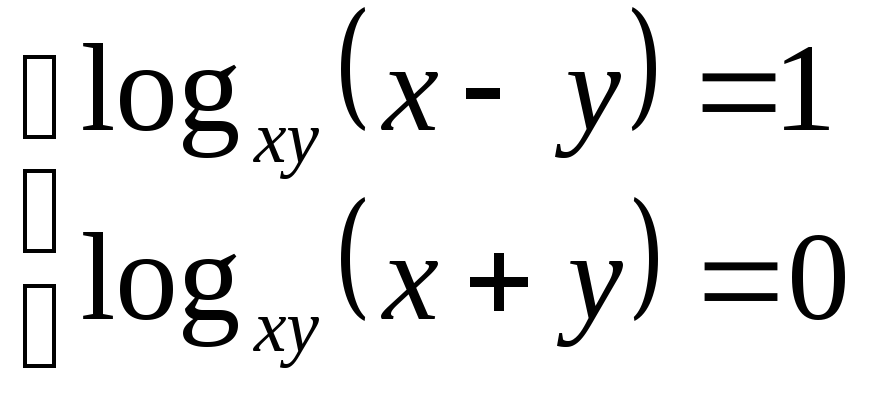
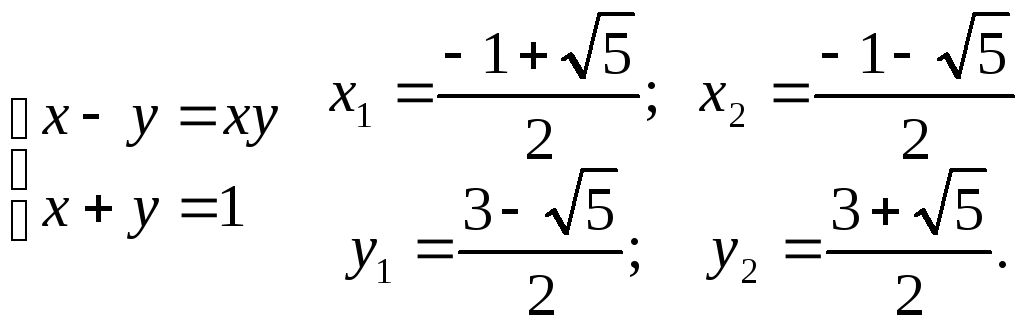
Другий розв’язок не задовольняє рівняння
Приклад.
З
першого рівняння знаходимо
.
З
системи рівнянь
знаходимо
.
Приклад.
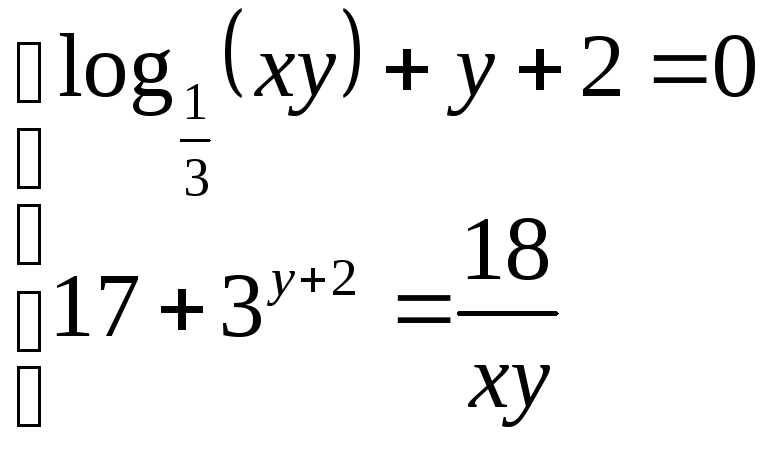
З
першого рівняння знаходимо
,
.
Друге значення
не задовольняє умові
.
.
Питання для самоперевірки
1. Графіки показових і логарифмічних функцій.
2.
Знайти границі:
.
3. Властивості показових функцій.
4. Властивості логарифмів.
5. Способи розв’язання логарифмічних рівнянь.
6. Способи розв’язання показових рівнянь.
Вправи для самостійного розв’язування
1. Обчислити
(10)