Варіант 2

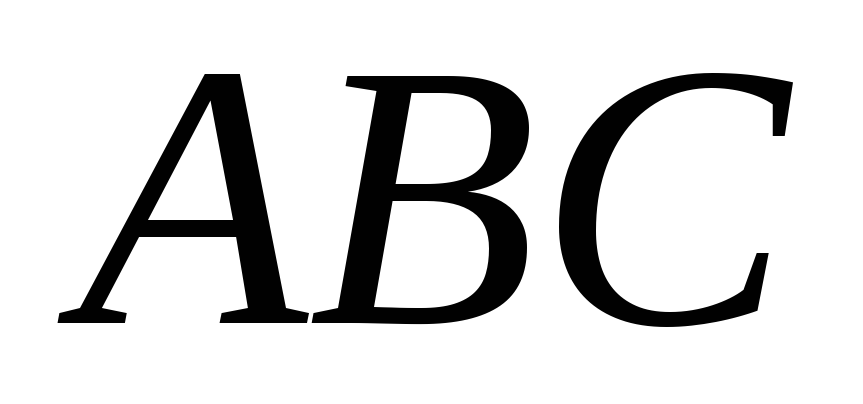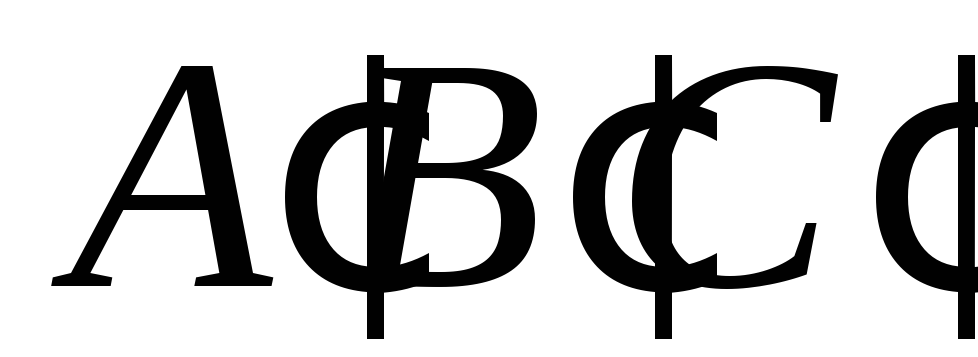1. Дано конфігурацію Дезарга: тривершинники і , пряму Дезарга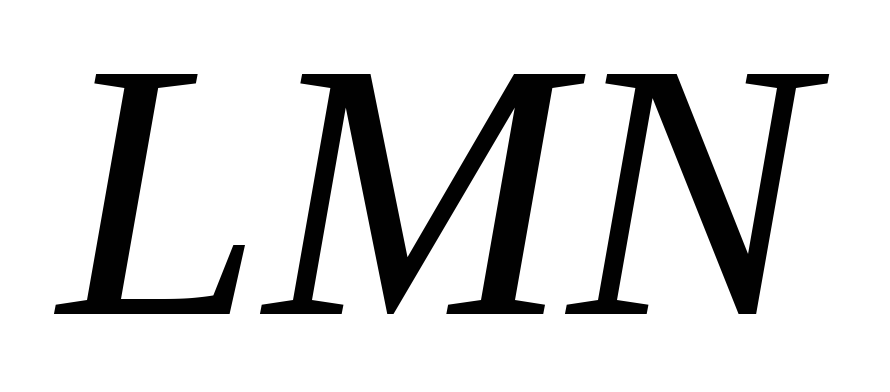 і точку Дезарга 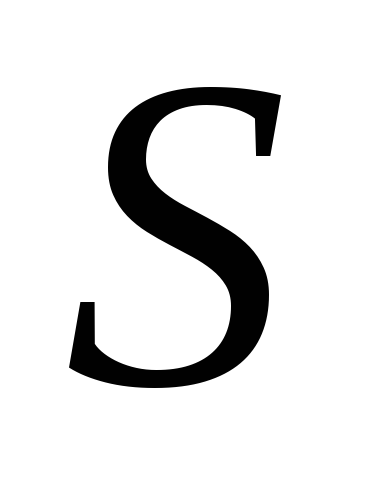. Прийнявши точку за точку Дезарга, знайти для цього випадку відповідні тривершинники і пряму Дезарга.

2. Визначити значення одного із складних відношень, які утворюють осі прямокутної системи координат з прямими: .

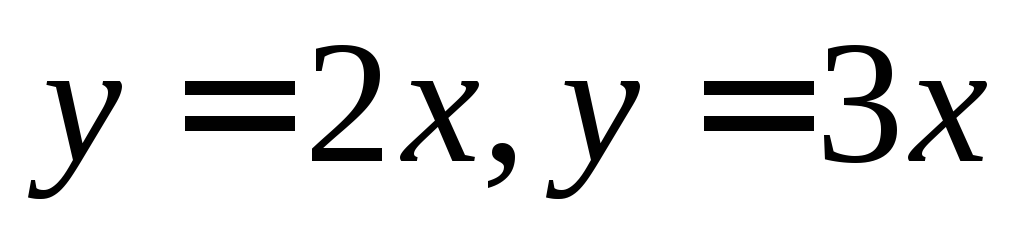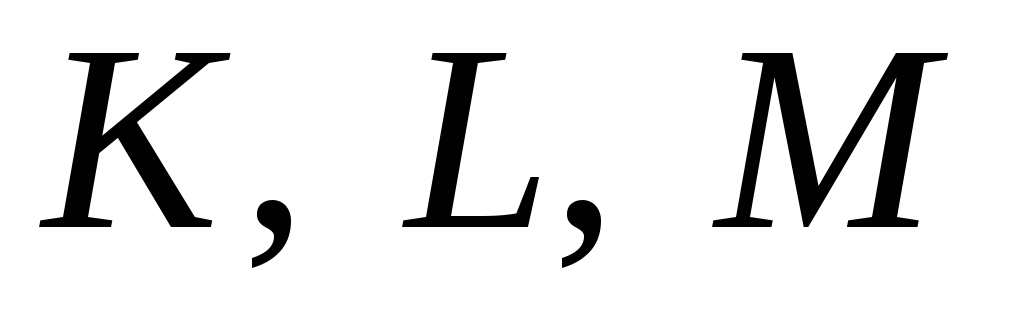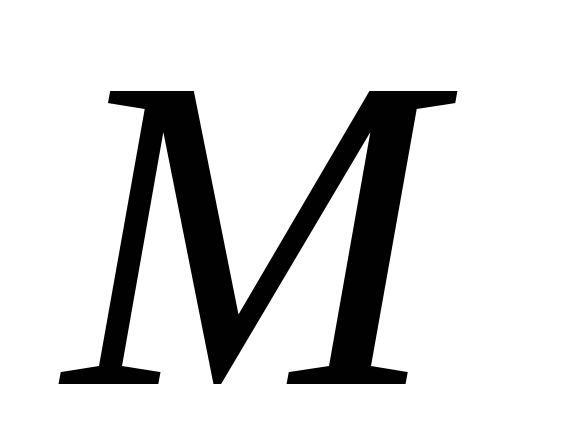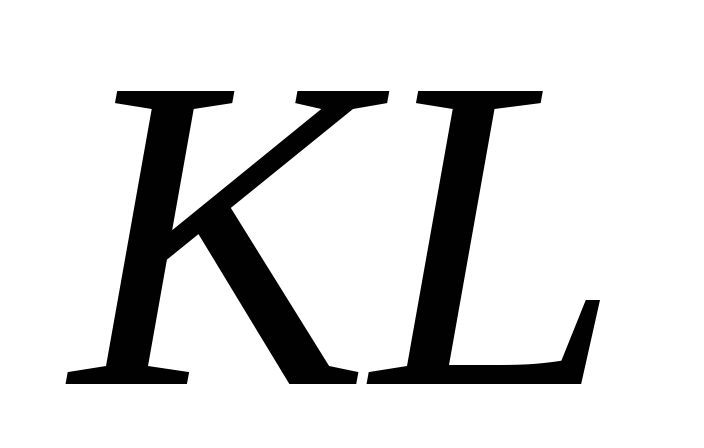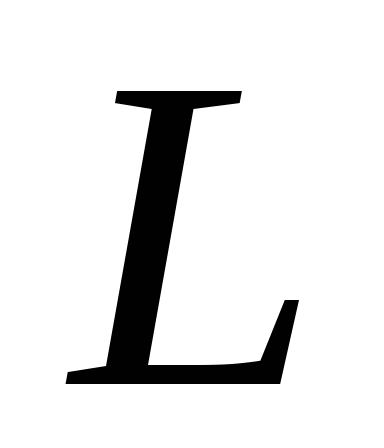3. Дано точки на прямій (точка– поза відрізком). Побудувати точку, гармонічно спряжену з точкоювідносно точокі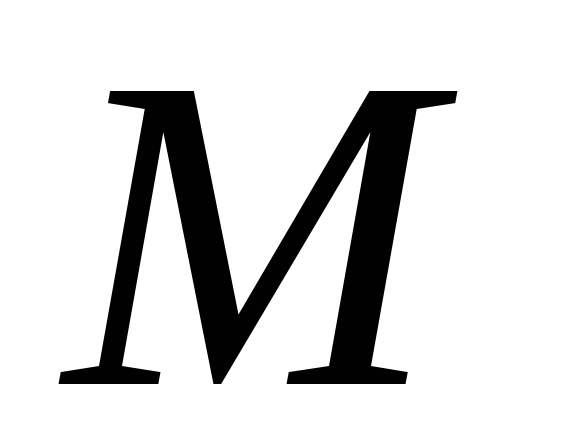. Задачу розв’язати трьома способами: використовуючи властивості бісектрис внутрішнього і зовнішнього кутів трикутника, подібність трикутників та гармонічну властивість повного чотиривершинника.

4. На площині дані дві паралельні прям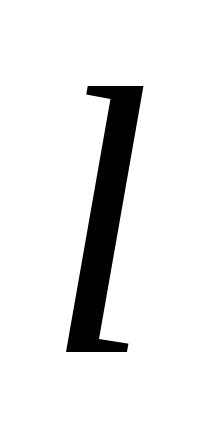і і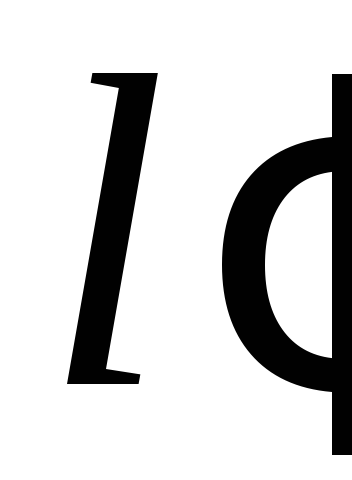та відрізок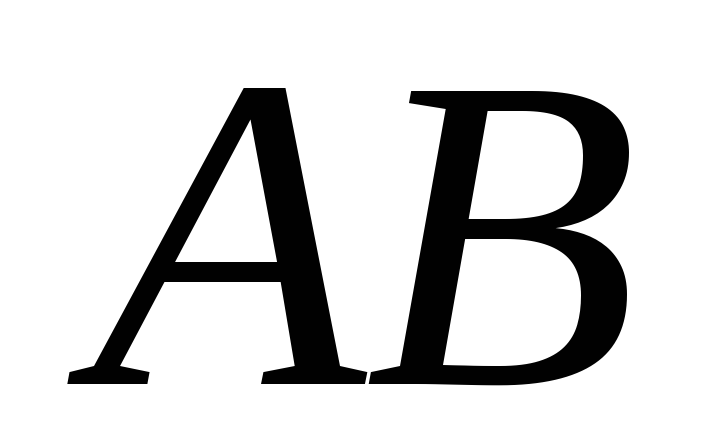на прямій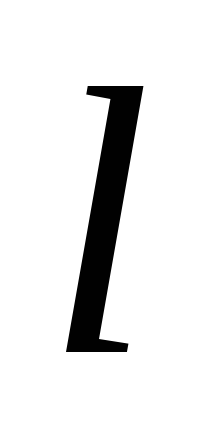. Використовуючи тільки односторонню лінійку, поділити відрізок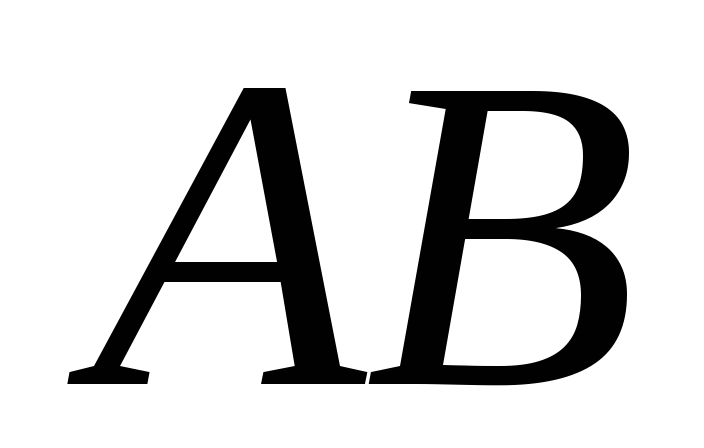навпіл.

5. Криву другого порядку задано чотирма точками 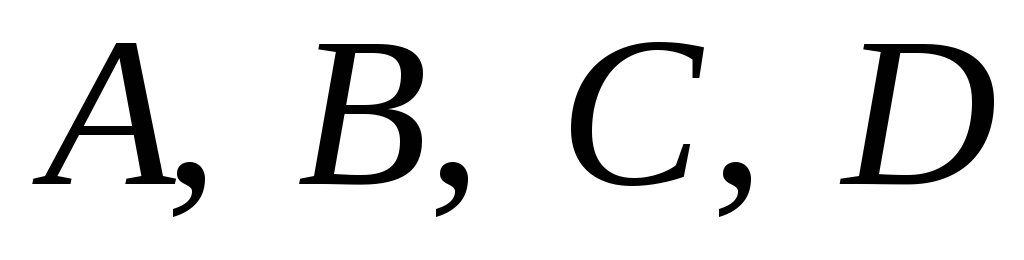і дотичною в точці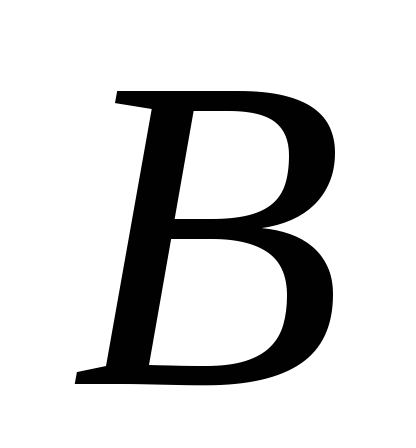. Побудувати яку-небудь п’яту точку цієї кривої.

6. Застосувати теорему Бріаншона до чотиристоронника, описаного навколо кривої другого порядку, приймаючи дві його протилежні сторони за подвійні.

7. Дано (накреслено) криву другого порядку і пряму 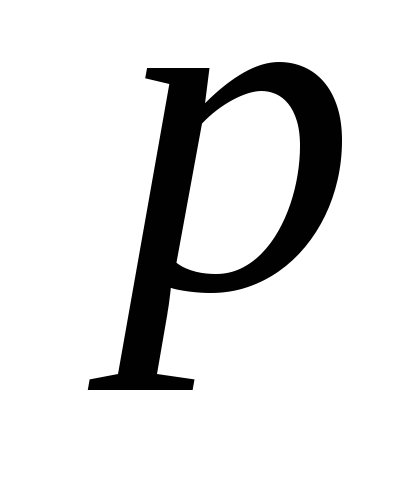, яка не має спільних точок з даноюкривою. Побудувати полюс 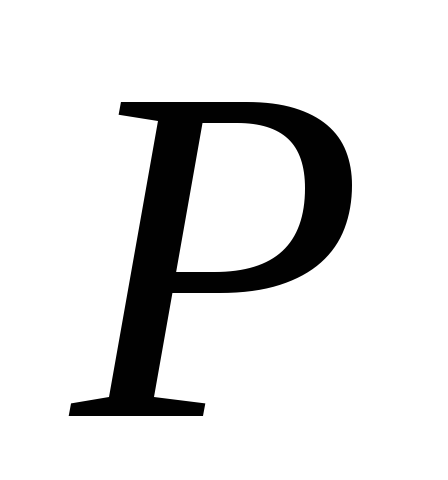прямої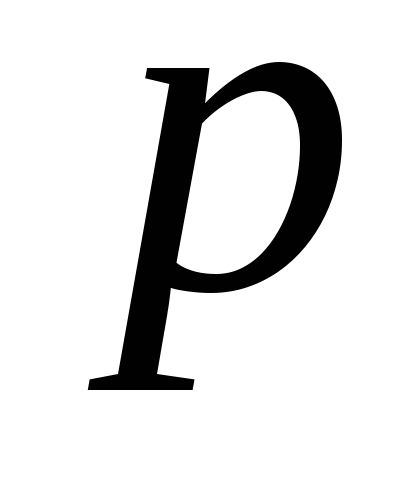відносно даної кривої.

Варіант 3

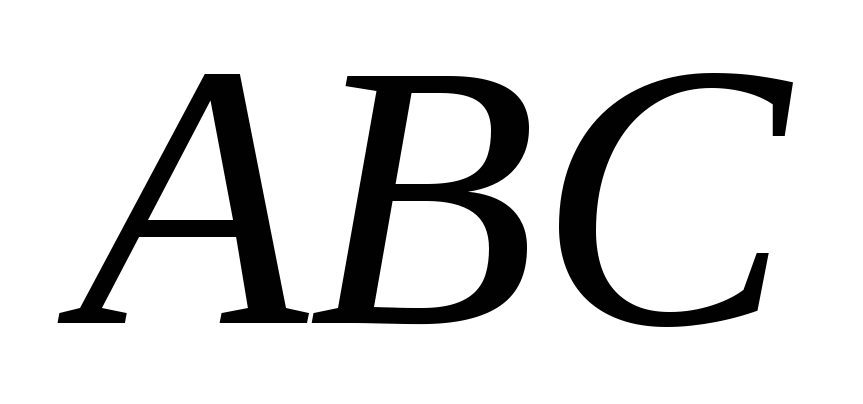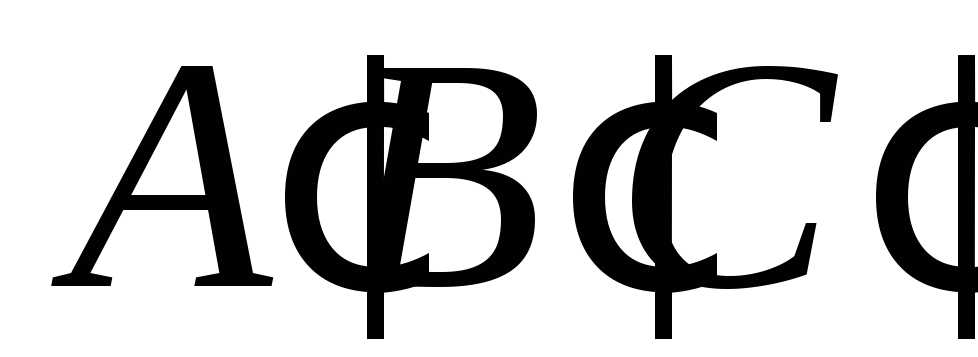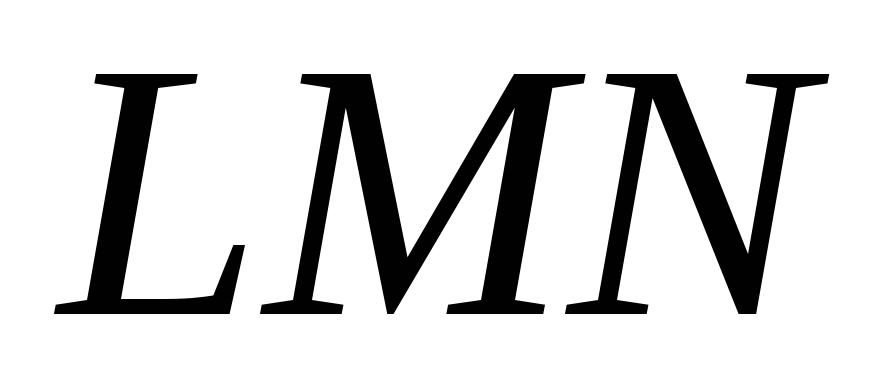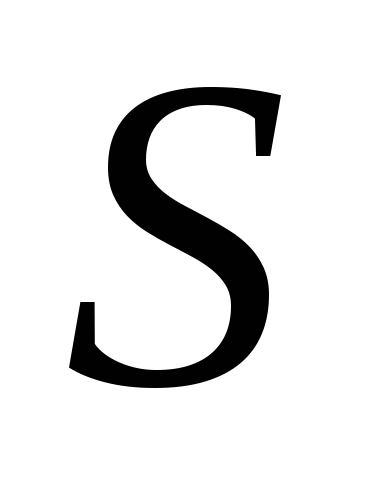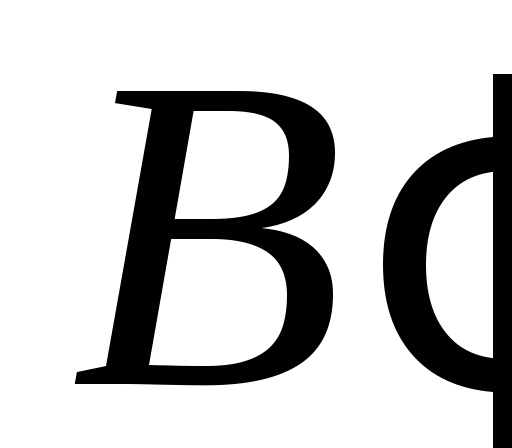1. Дано конфігурацію Дезарга: тривершинники і , пряму Дезарга і точку Дезарга . Прийнявши точку за точку Дезарга, знайти для цього випадку відповідні тривершинники і пряму Дезарга.

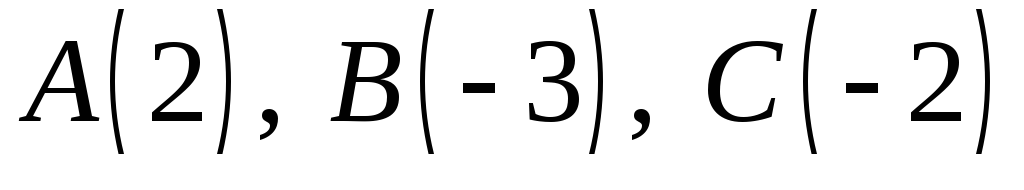2. Дано три точки декартовими координатами на прямій. Знайти четверту гармонічнуточку, спряжену з точкою .

3. Дано три прямі 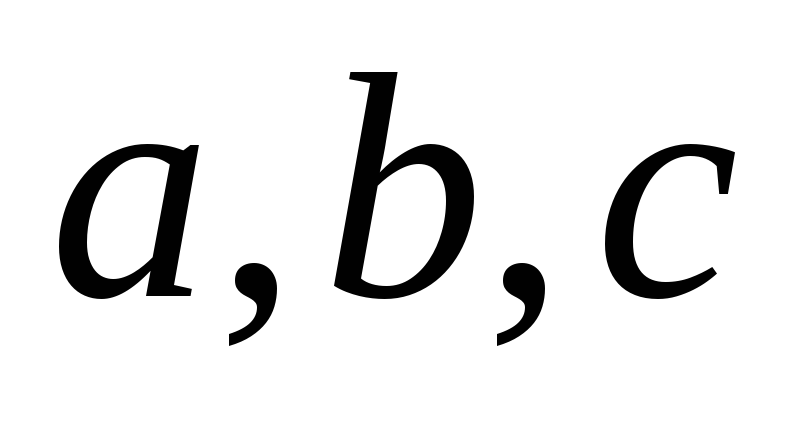одного пучка з невласним центром. Побудувати четверту пряму, гармонічно спряжену з прямою.

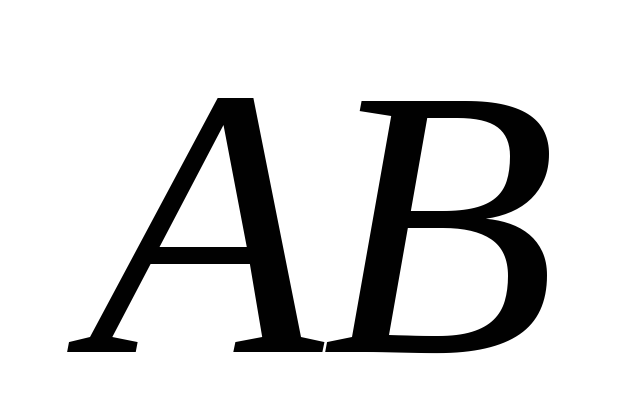4. На прямій дано відрізокі його середину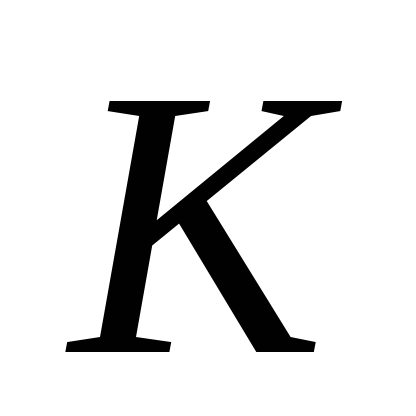. Використовуючи тільки односторонню лінійку, через дану точкупровести пряму, паралельну прямій.

5. Дано конфігурацію Паскаля-Паппа: 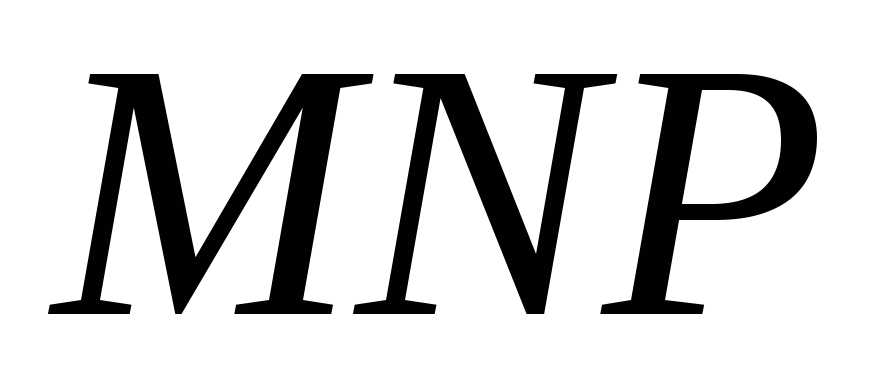– пряма Паскаля,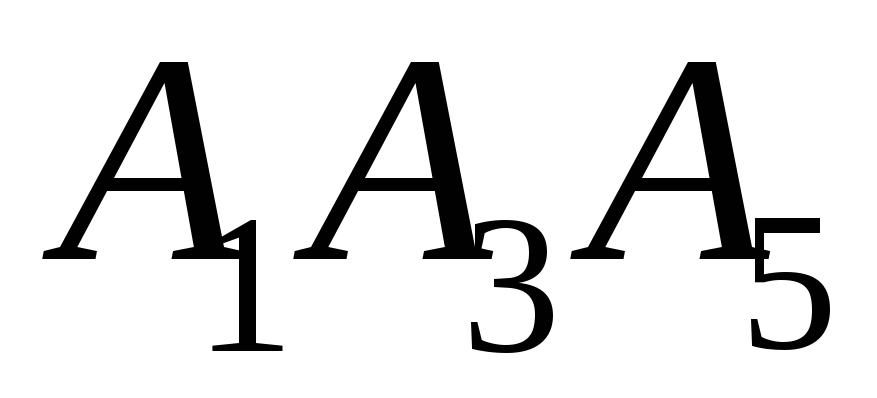та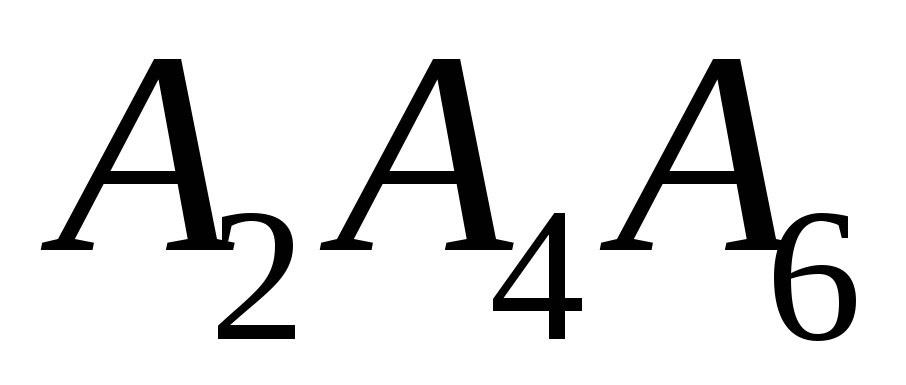– прямолінійні ряди, на які розпалась крива другого порядку. Прийнявши прямуза пряму Паскаля, знайти відповідні для цього випадку прямолінійні ряди.

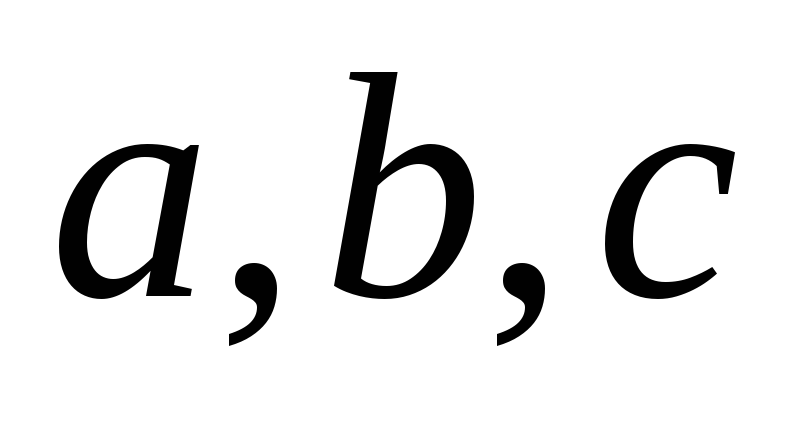6. Дано три дотичні до кривої другого порядку і точки дотику дотичних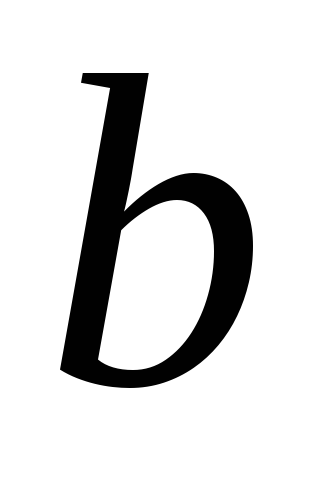і. Побудувати ще яку-небудь дотичну до цієї кривої.

7. Дано (накреслено) криву другого порядку і точку 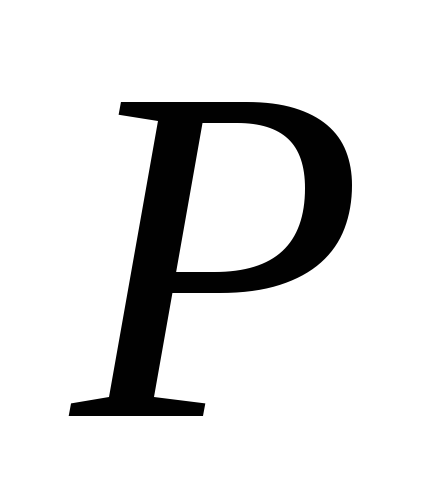поза кривою. Побудувати різними способами дотичні до даної кривої з точки.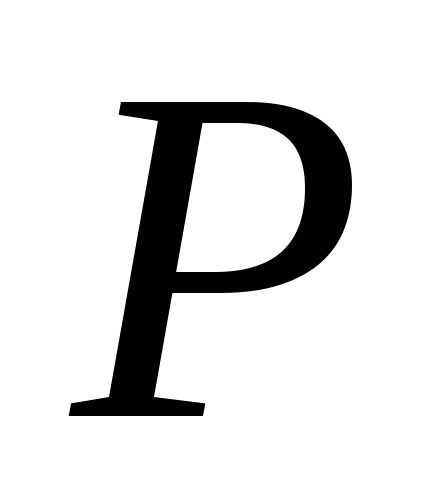

Варіант 4

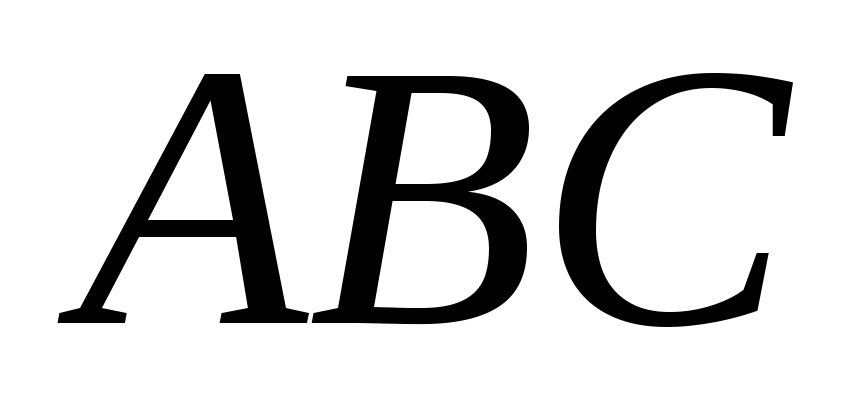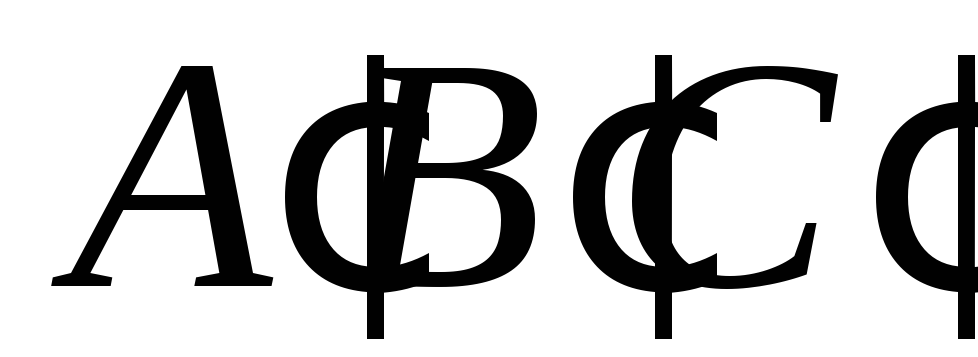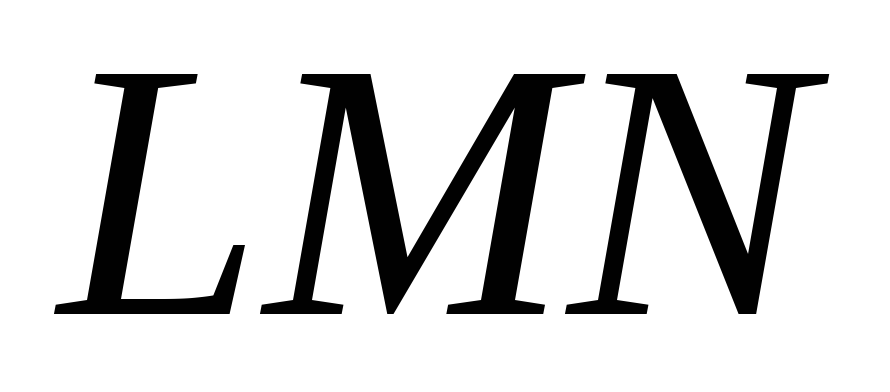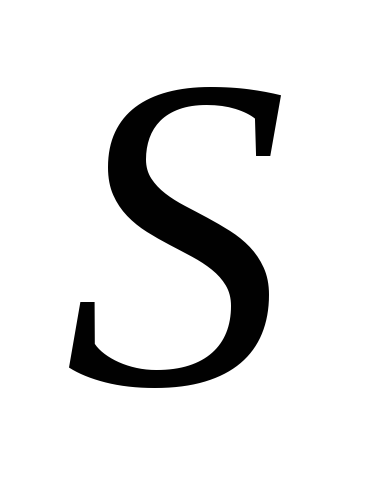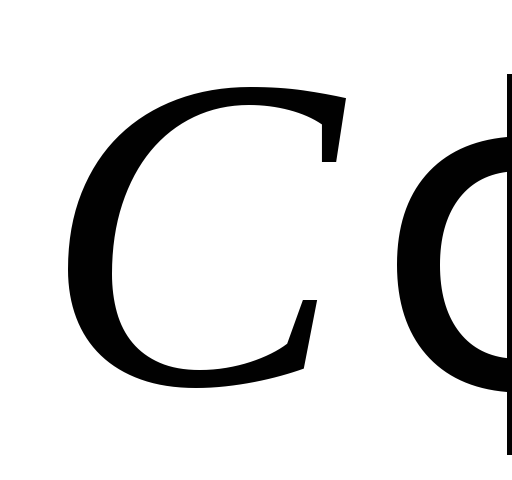1. Дано конфігурацію Дезарга: тривершинники і , пряму Дезарга і точку Дезарга . Прийнявши точку за точку Дезарга, знайти для цього випадку відповідні тривершинники і пряму Дезарга.

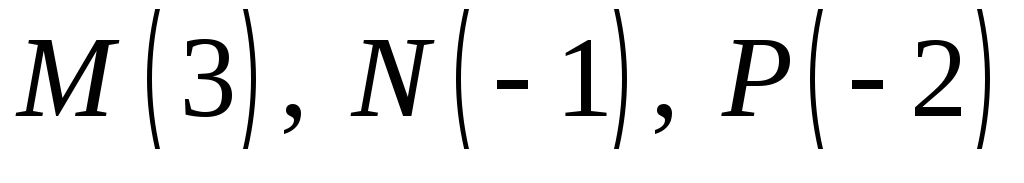2. Дано три точки декартовими координатами на прямій. Знайти четверту гармонічну точку, прийнявши за спряжену точку.

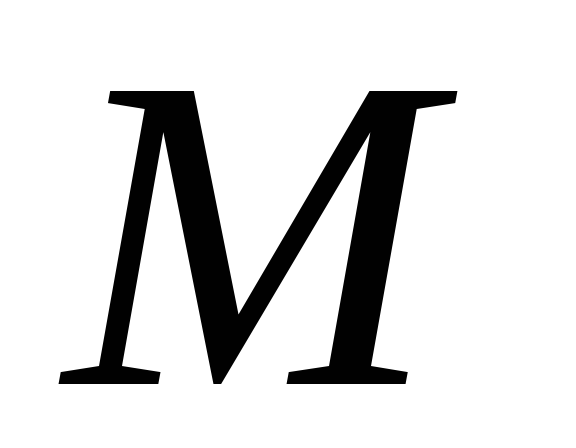3. Дано три прямі 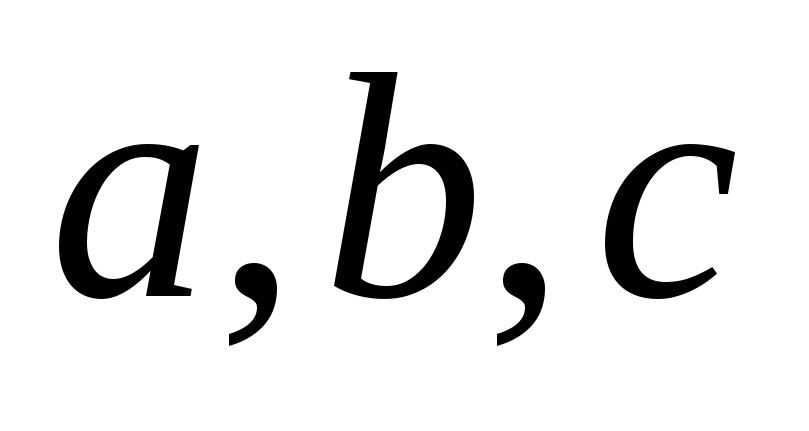одного пучка з власним центром. Побудувати четверту пряму, гармонічно спряжену з прямою.

4. Дано дві паралельні прям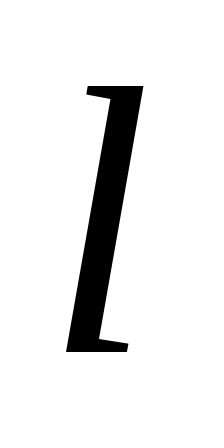і і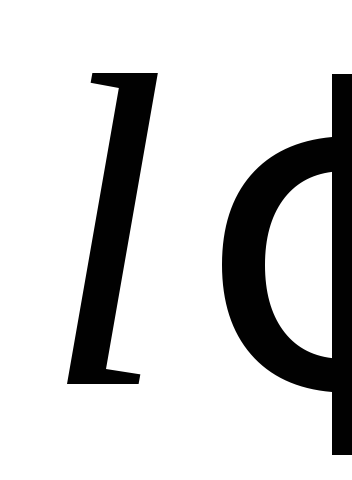та точку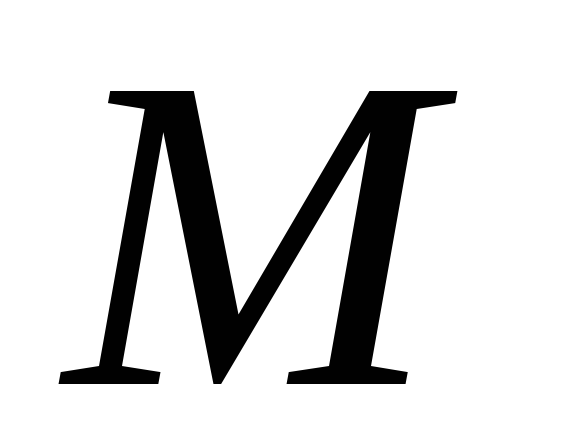, яка не належить цим прямим. Використовуючи тільки односторонню лінійку, провести через точку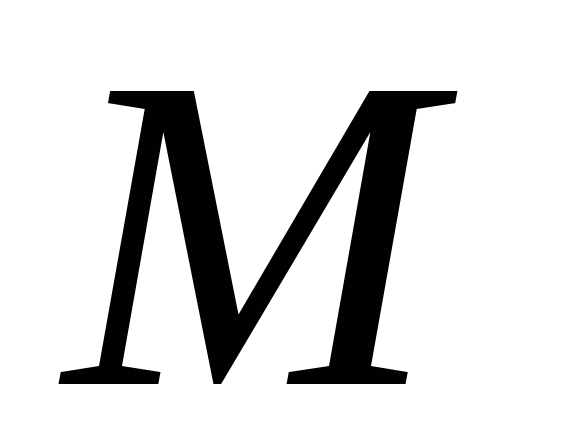пряму, паралельну даним прямим.

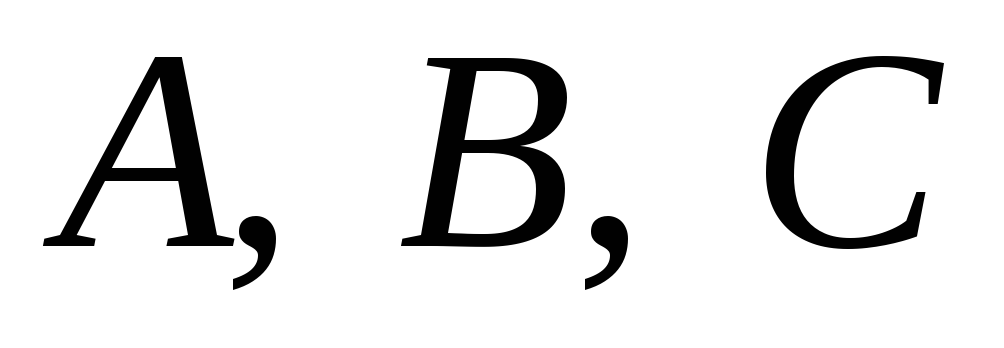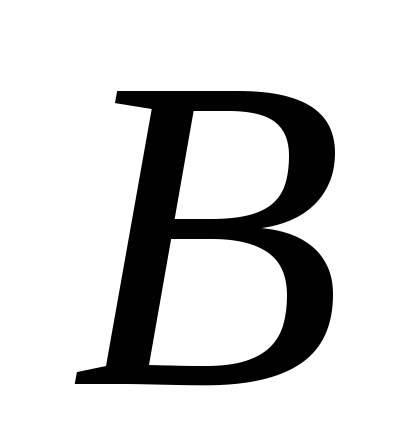5. Дано три точки кривої другого порядку і дотичні в точкахі. Побудувати дотичну до кривої в точці.

6. Дано п’ять дотичних 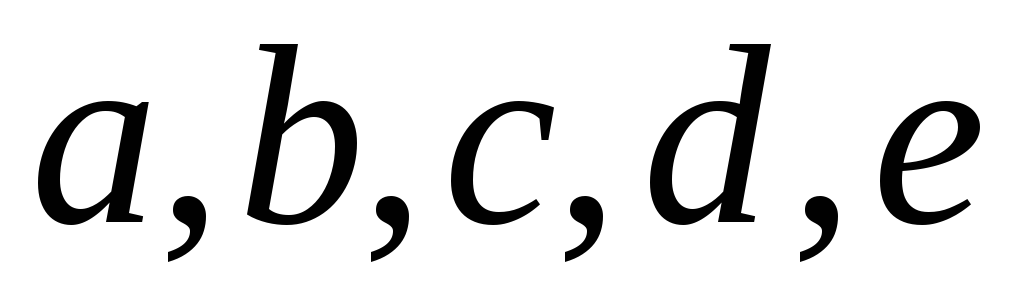до кривої другого порядку. Побудувати точку дотику прямої.

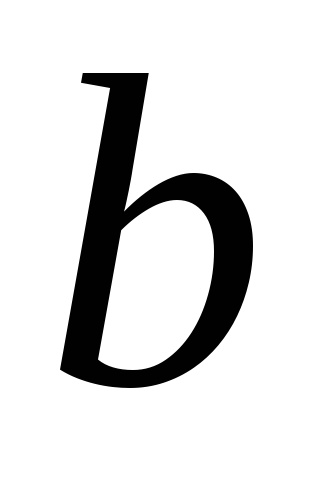7. Дано (накреслено) криву другого порядку і точку 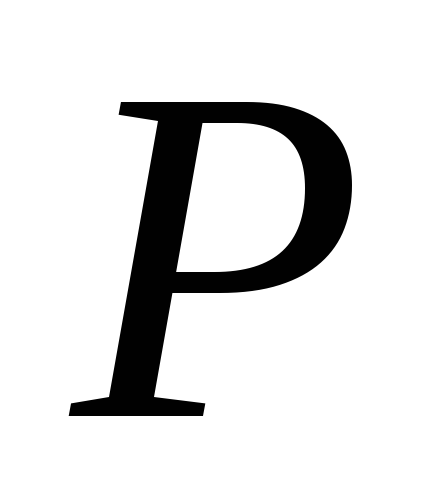поза кривою. Побудувати поляру точки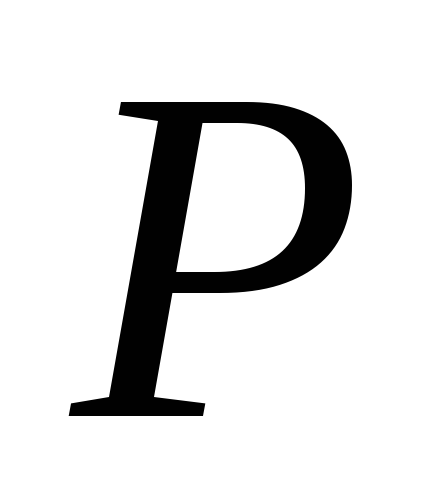відносно даної кривої.