
- •Змістовий модуль 2 «Методи зображення просторових фігур на площині» Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 4
- •Варіант 5
- •Варіант 6
- •Варіант 7
- •Варіант 8
- •Варіант 9
- •Варіант 10
- •Змістовий модуль 3 «Елементи проективної геометрії» Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 4
- •Варіант 5
- •Варіант 6
- •Варіант 7
- •Варіант 8
- •Варіант 9
- •Варіант 10
Варіант 8
Побудувати зображення кола, описаного навколо квадрата.
Побудувати зображення циліндра, вписаного в правильну трикутну піраміду, якщо висота циліндра дорівнює половині висоти піраміди.
Побудувати переріз п’ятикутної призми площиною
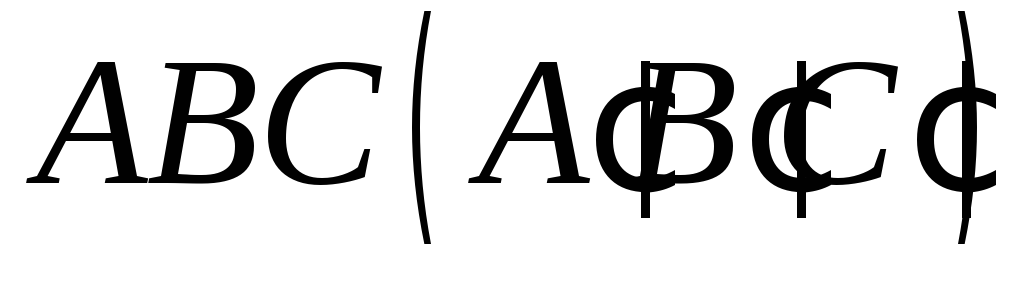 ,
якщо точка
,
якщо точка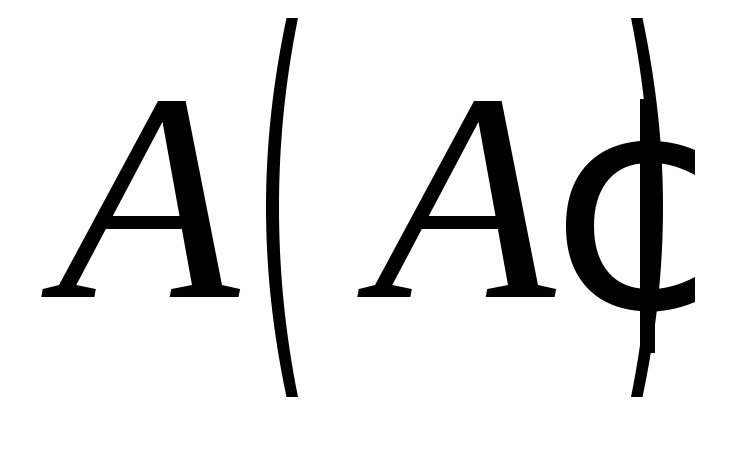 знаходиться в площині нижньої основи
(поза контуром основи), точка
знаходиться в площині нижньої основи
(поза контуром основи), точка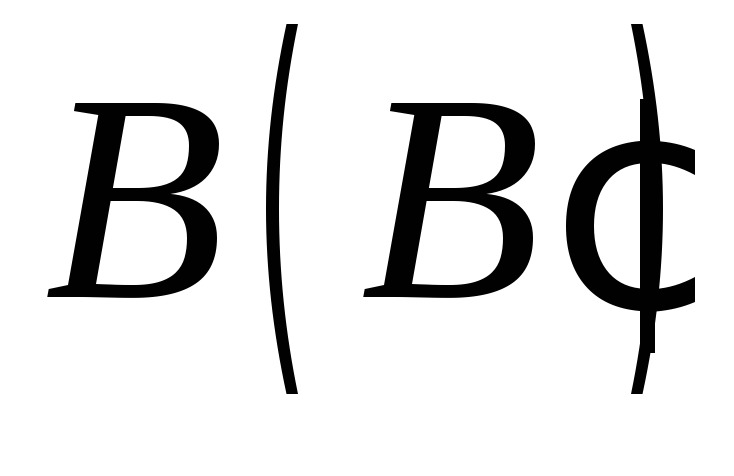 – на бічній грані, точка
– на бічній грані, точка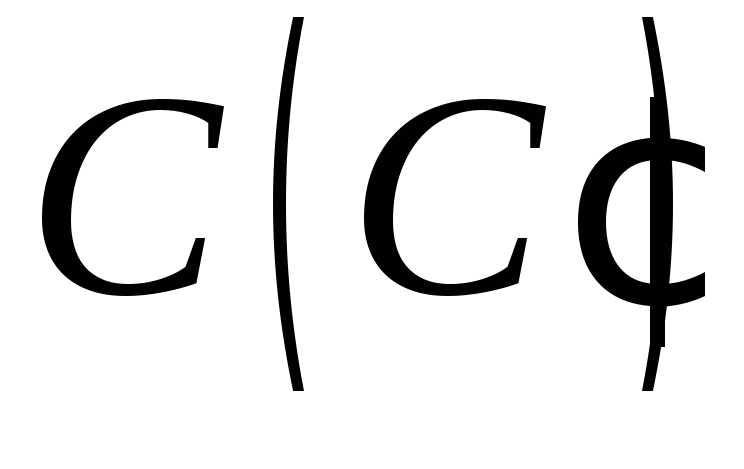 – на бічному ребрі суміжної бічної
грані (методом слідів).
– на бічному ребрі суміжної бічної
грані (методом слідів).Побудувати переріз чотирикутної піраміди площиною
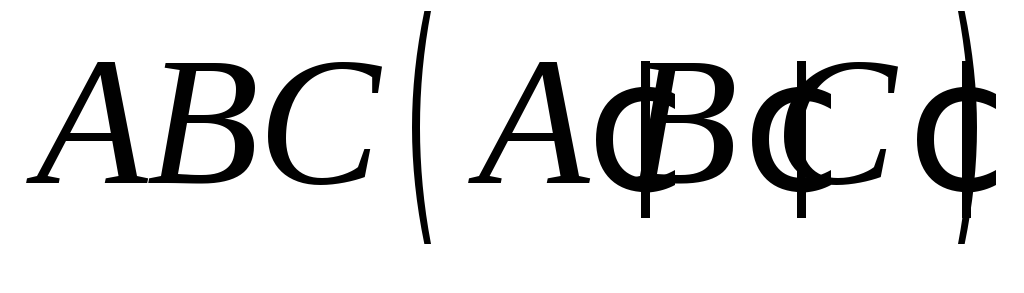 ,
якщо точка
,
якщо точка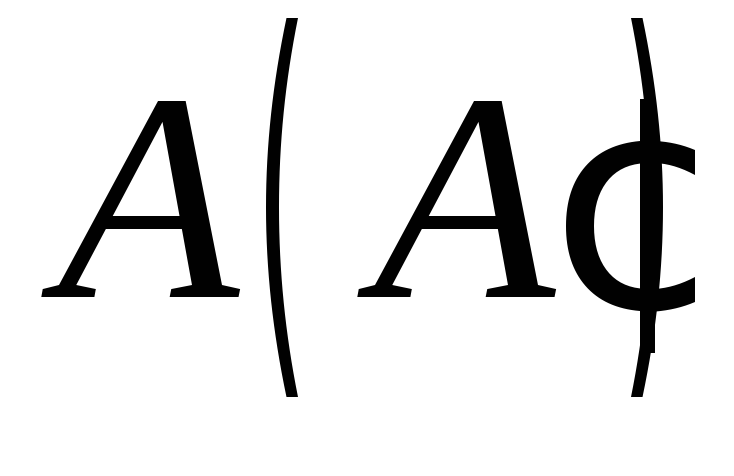 знаходиться на ребрі основи, точка
знаходиться на ребрі основи, точка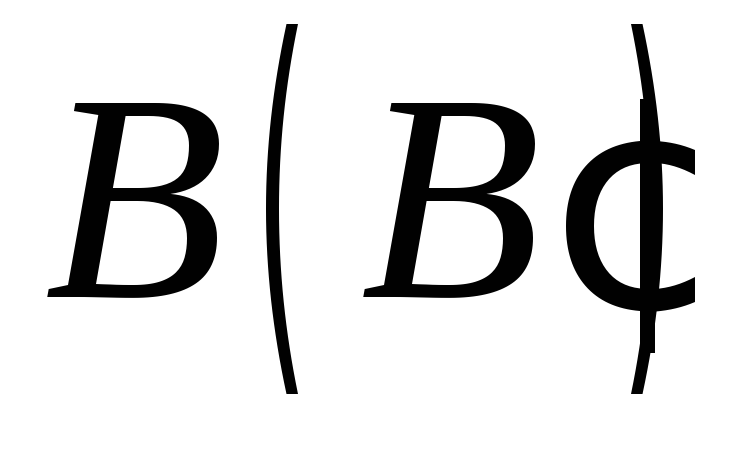 – поза пірамідою, а точка
– поза пірамідою, а точка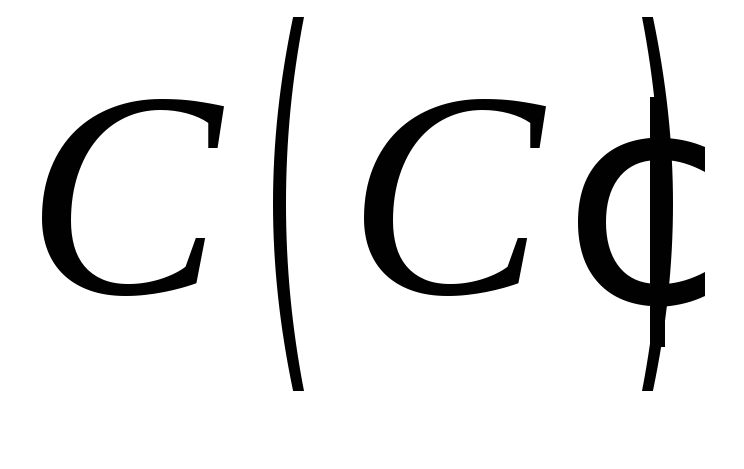 – всередині піраміди (методом внутрішнього
проектування).
– всередині піраміди (методом внутрішнього
проектування).На бічній грані чотирикутної призми дано відрізок
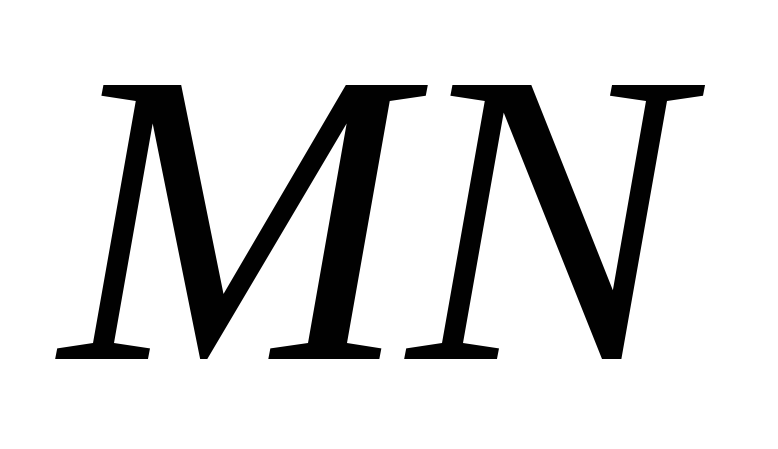 . Знайти точки зустрічі прямої
. Знайти точки зустрічі прямої з площинами інших граней призми.
з площинами інших граней призми.Побудувати переріз куба
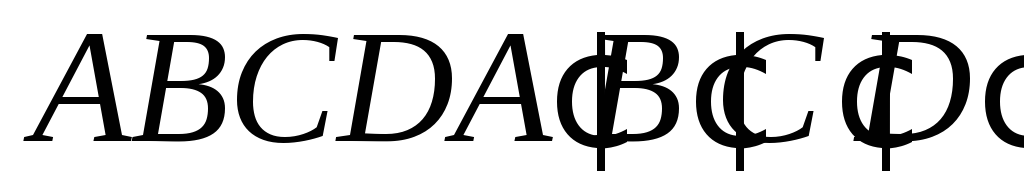 площиною, яка проходить через середини
реберC′D′,
AВ
і A′D′.
площиною, яка проходить через середини
реберC′D′,
AВ
і A′D′.Дано зображення рівнобедреного трикутника
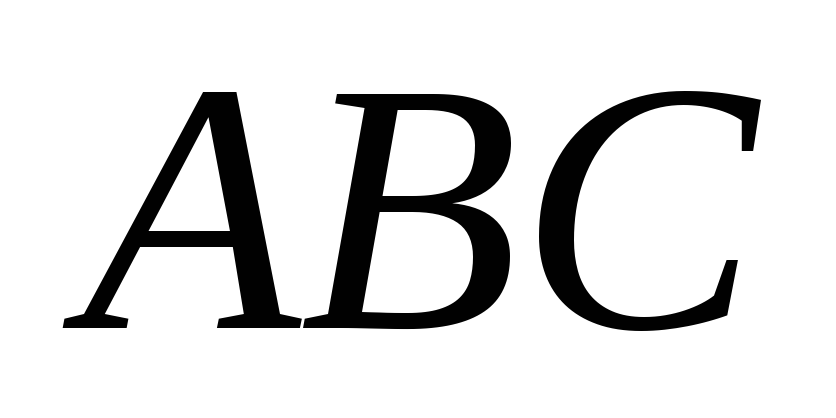 ,
в якому
,
в якому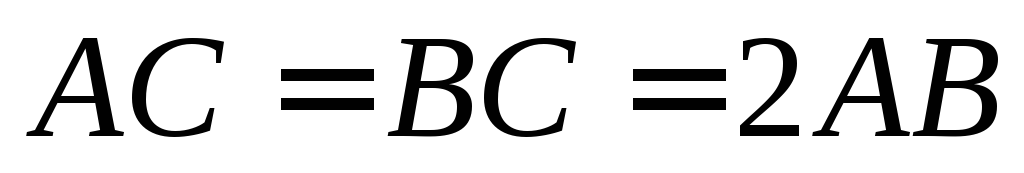 .
Побудувати зображення ортоцентра
трикутника
.
Побудувати зображення ортоцентра
трикутника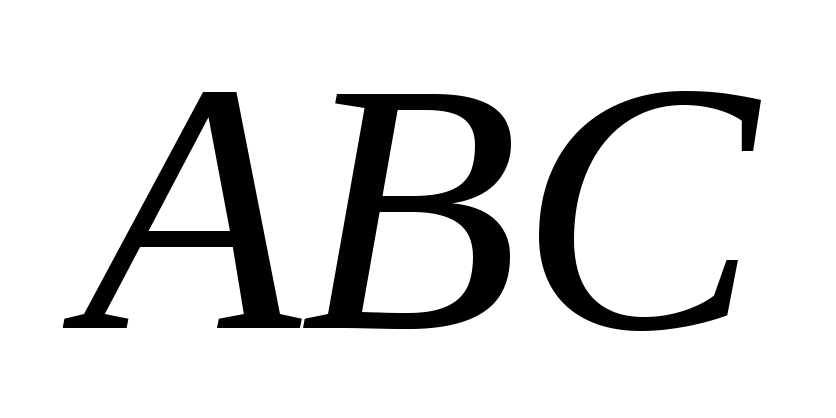 .
.
Варіант 9
Побудувати зображення рівнобедреного прямокутного трикутника, вписаного в коло.
Побудувати зображення правильної чотирикутної призми, описаної навколо циліндра.
Побудувати переріз п’ятикутної призми площиною
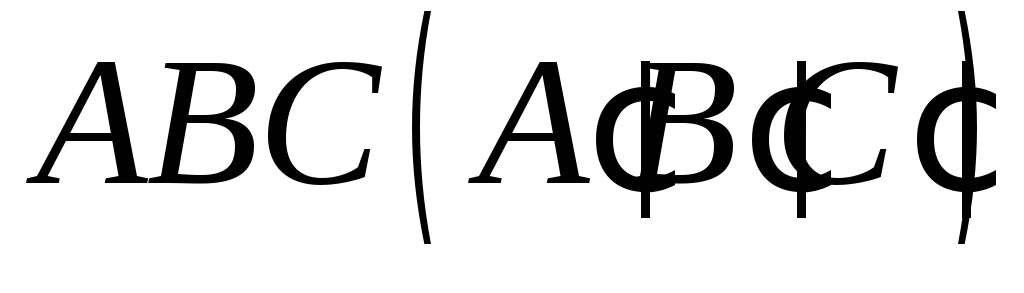 ,
якщо точка
,
якщо точка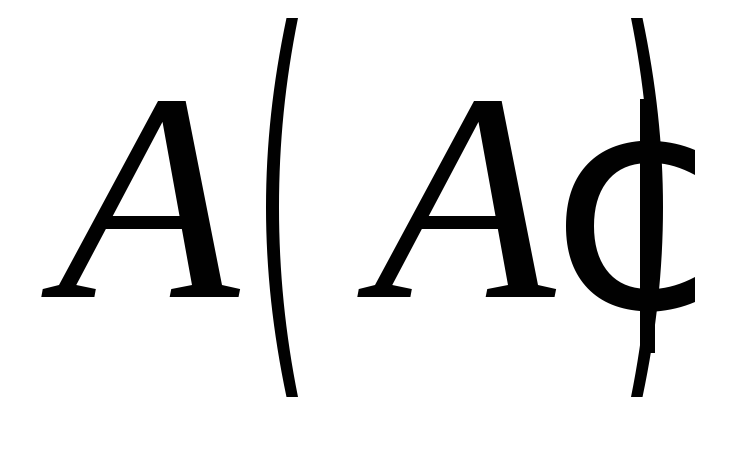 знаходиться на стороні верхньої основи,
точки
знаходиться на стороні верхньої основи,
точки і
і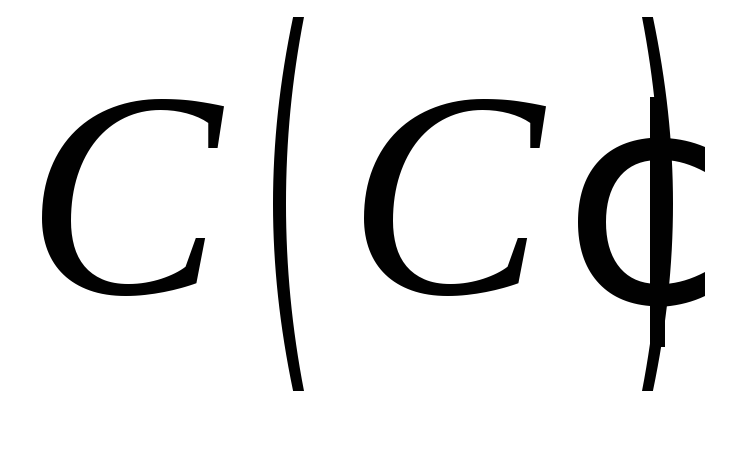 – на суміжних бічних гранях (методом
слідів).
– на суміжних бічних гранях (методом
слідів).Побудувати переріз чотирикутної піраміди площиною
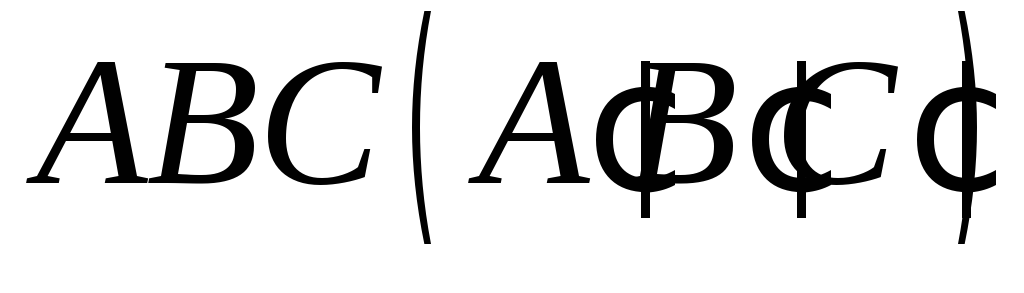 ,
якщо точки
,
якщо точки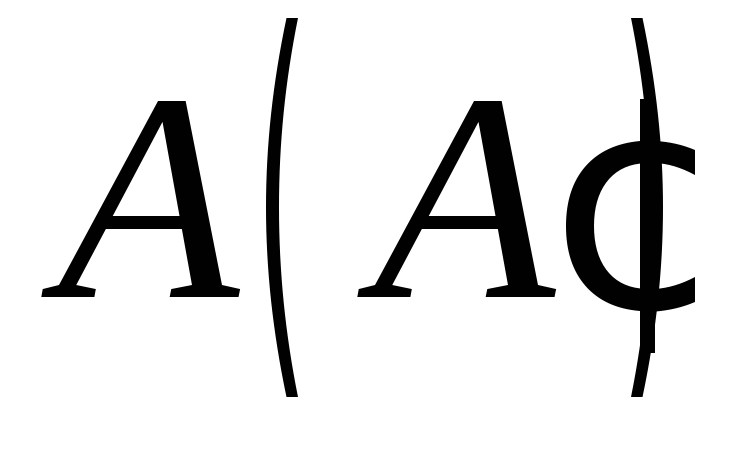 і
і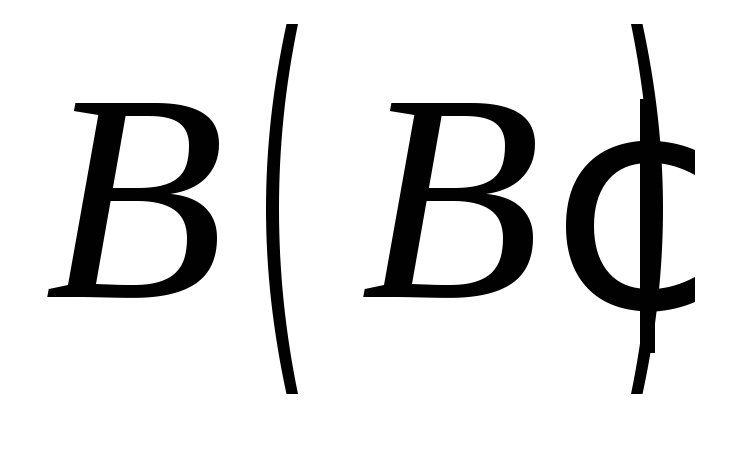 знаходяться на протилежних бічних
ребрах, а точка
знаходяться на протилежних бічних
ребрах, а точка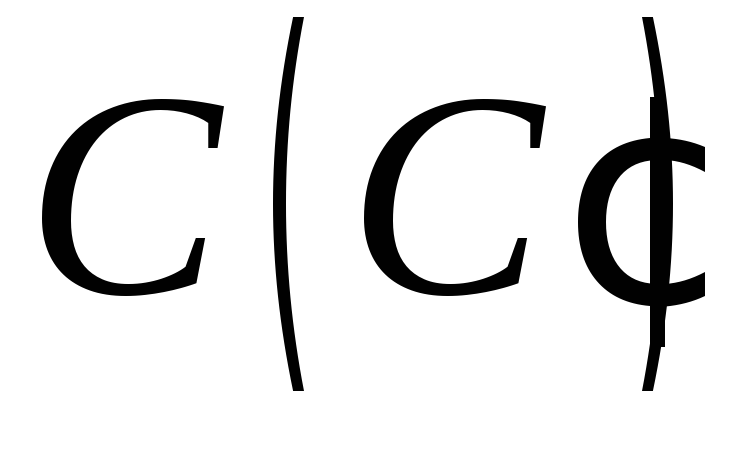 – всередині піраміди (методом
внутрішнього проектування.).
– всередині піраміди (методом
внутрішнього проектування.).На бічній грані п’ятикутної піраміди дано відрізок
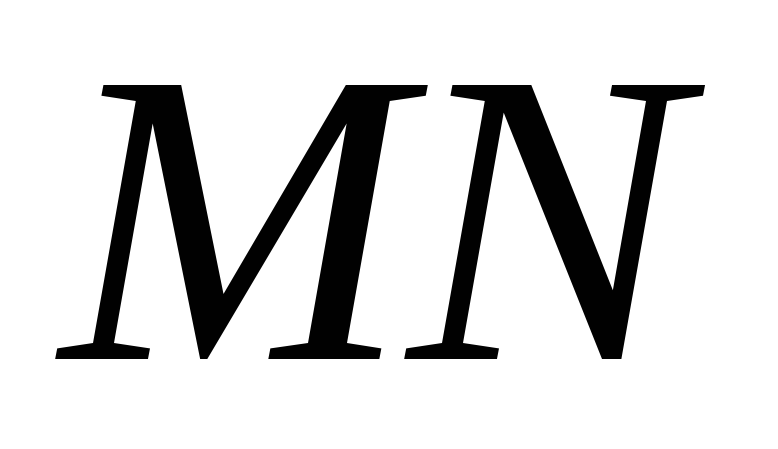 . Знайти точки зустрічі прямої
. Знайти точки зустрічі прямої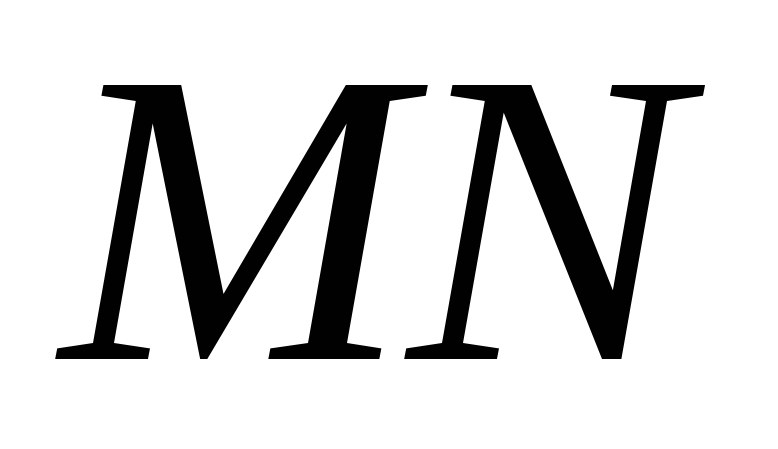 з площинами інших граней піраміди.
з площинами інших граней піраміди.Побудувати переріз куба
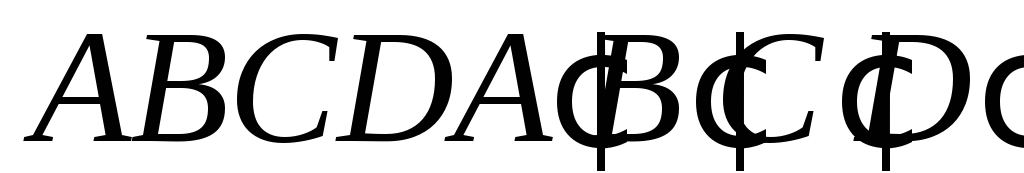 площиною, яка проходить через вершинунижньої основиD′тасередини ребер А′B′іСD.
площиною, яка проходить через вершинунижньої основиD′тасередини ребер А′B′іСD.Дано зображення правильного тетраедра
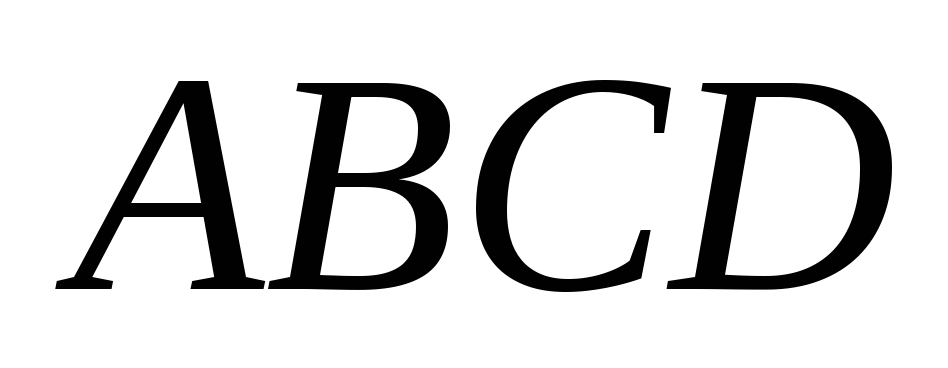 .
Побудувати спільний перпендикуляр
його протилежних ребер
.
Побудувати спільний перпендикуляр
його протилежних ребер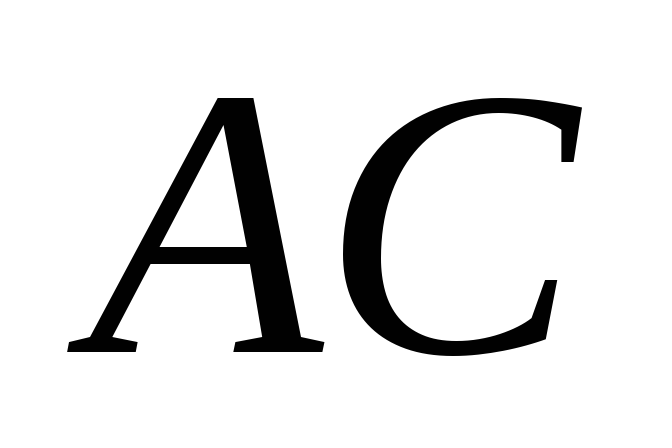 і
і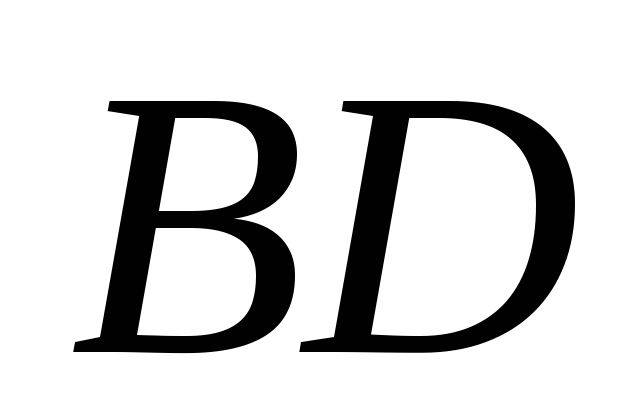 .
.
Варіант 10
Побудувати зображення рівнобедреного прямокутного трикутника, описаного навколо кола.
Побудувати зображення правильної чотирикутної призми, вписаної в циліндр.
Побудувати переріз п’ятикутної призми площиною
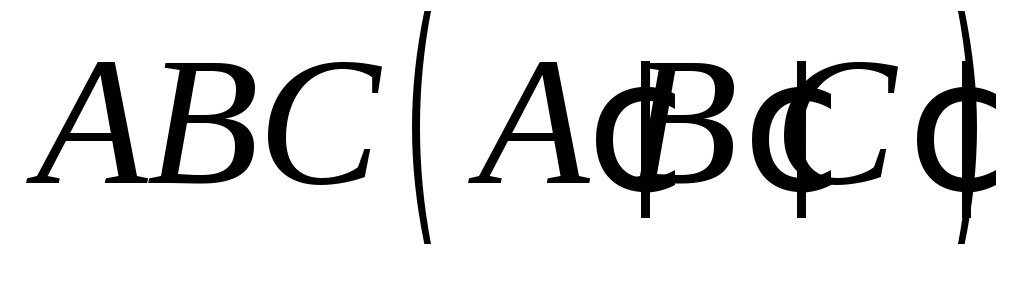 ,
якщо точка
,
якщо точка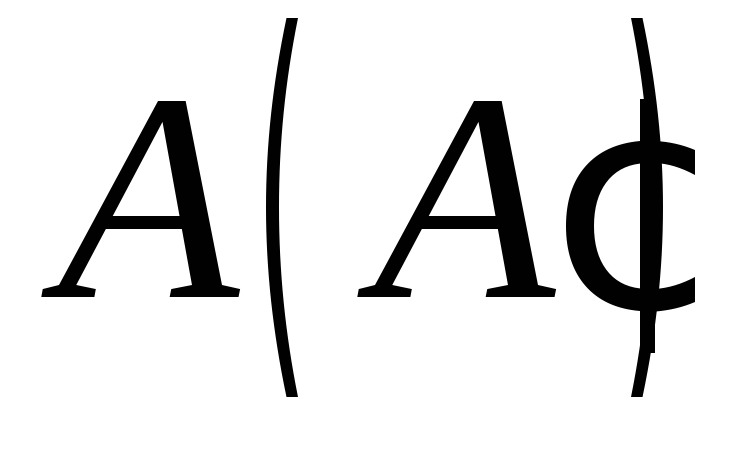 знаходиться в площині верхньої основи,
точка
знаходиться в площині верхньої основи,
точка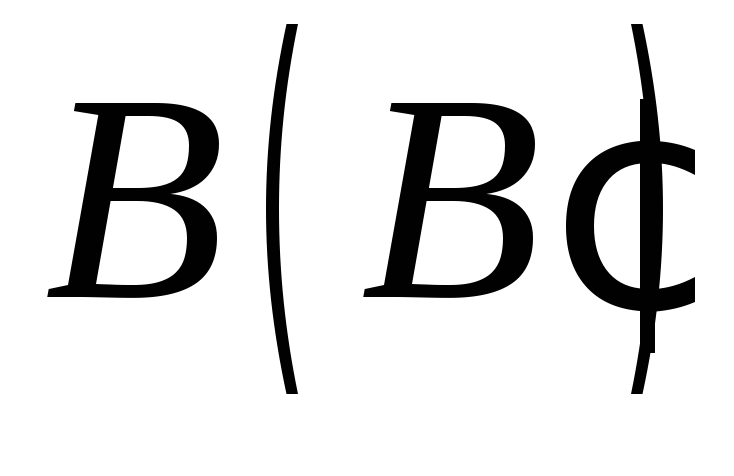 – на бічній грані, точка
– на бічній грані, точка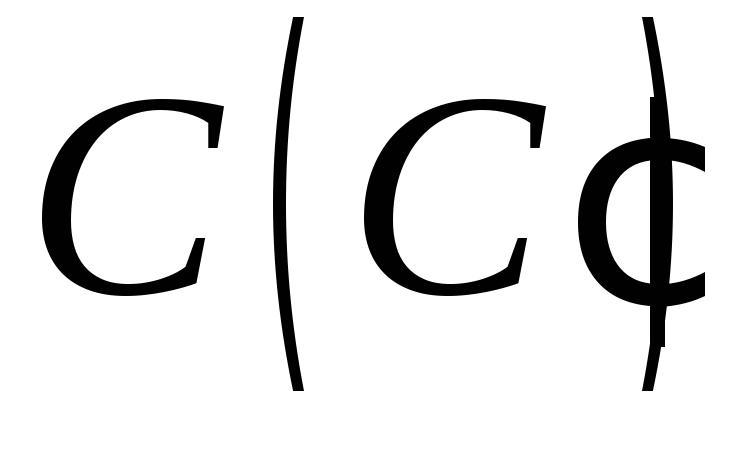 – на бічному ребрі суміжної бічної
грані (методом слідів).
– на бічному ребрі суміжної бічної
грані (методом слідів).Побудувати переріз чотирикутної піраміди площиною
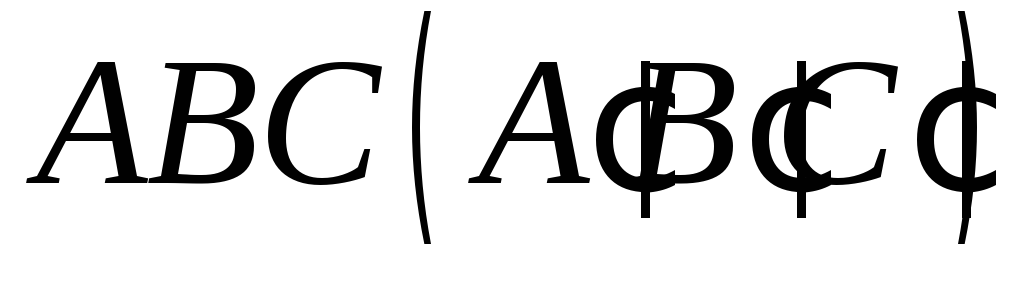 ,
якщо точка
,
якщо точка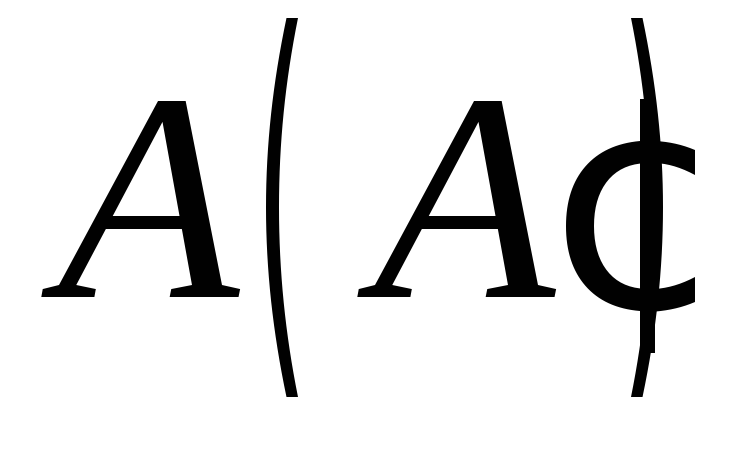 знаходиться на стороні нижньої основи,
точка
знаходиться на стороні нижньої основи,
точка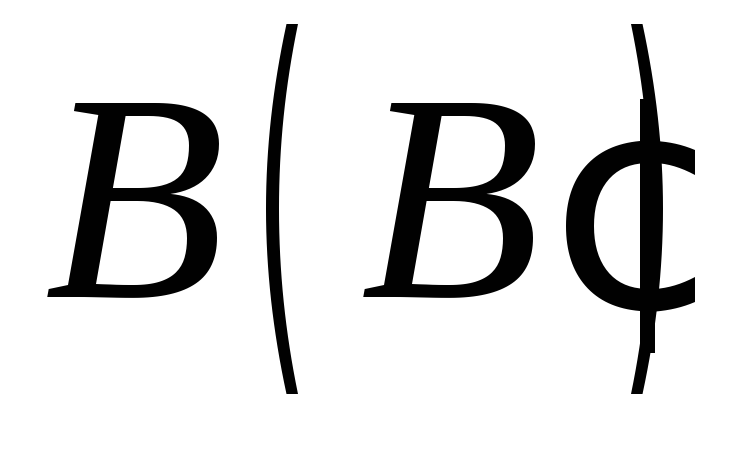 на бічній грані, а точка
на бічній грані, а точка – всередині піраміди (методом внутрішнього
проектування).
– всередині піраміди (методом внутрішнього
проектування).В площині основи п’ятикутної піраміди дано точку
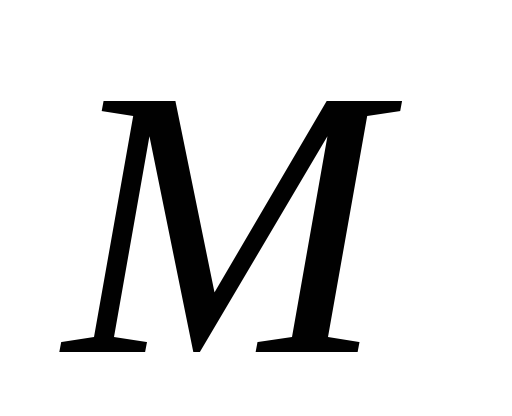 ,
а поза пірамідою – точку
,
а поза пірамідою – точку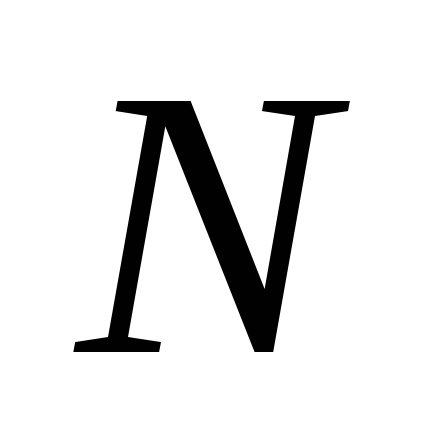 .
Побудувати точки перетину прямої
.
Побудувати точки перетину прямої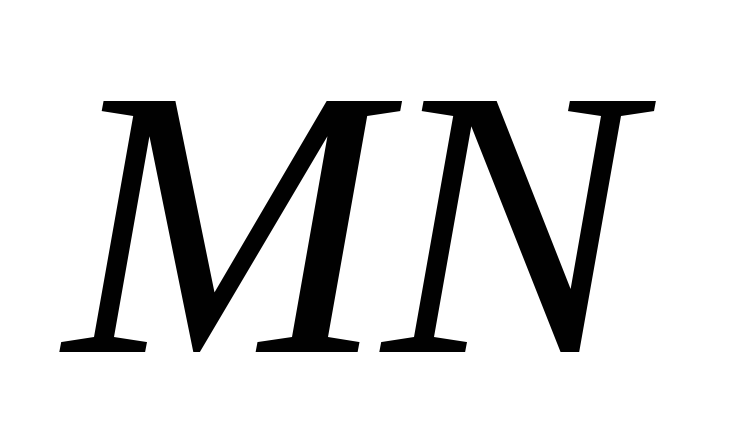 з площинами всіх граней піраміди.
з площинами всіх граней піраміди.Побудувати переріз куба
 площиною, заданою трьома точками
на ребрах АВ, CC′
і А′D′ .
площиною, заданою трьома точками
на ребрах АВ, CC′
і А′D′ .На діагоналі
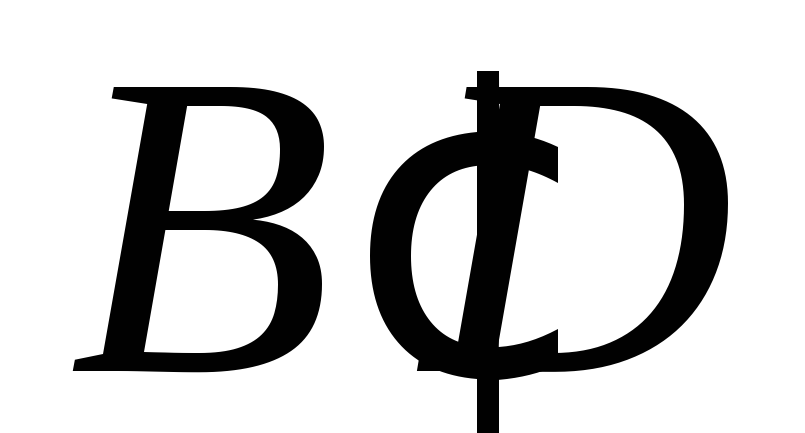 куба
куба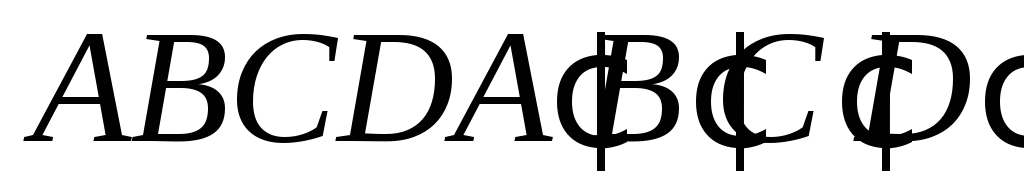 взято точку
взято точку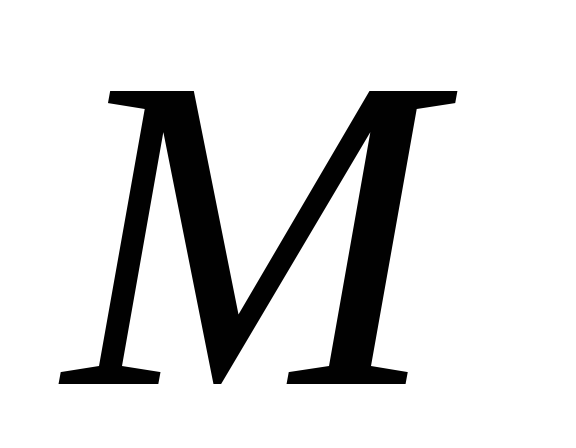 .
Побудувати зображення перпендикуляра,
який проведено з точки
.
Побудувати зображення перпендикуляра,
який проведено з точки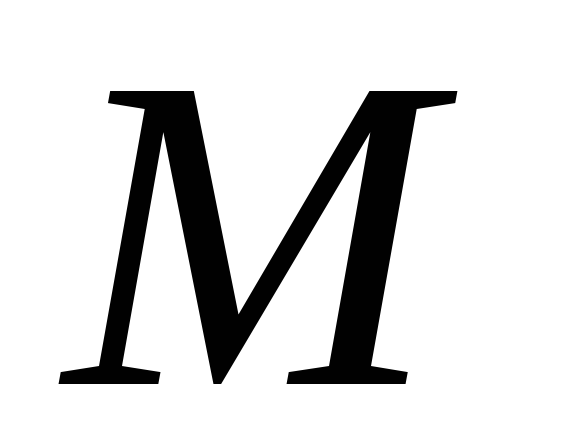 до площини
до площини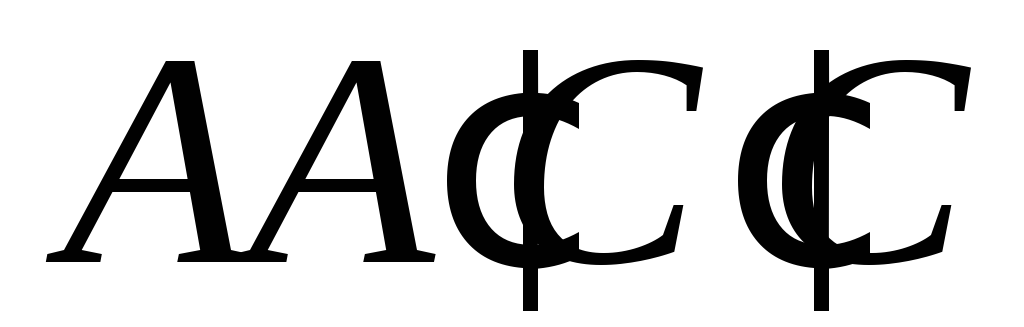 .
.
ІНДИВІДУАЛЬНЕ ЗАВДАННЯ 3
Змістовий модуль 3 «Елементи проективної геометрії» Варіант 1
Дано конфігурацію Дезарга: тривершинники
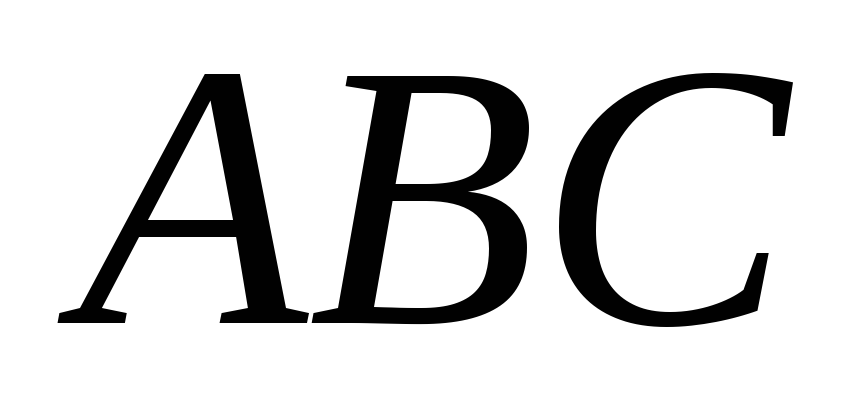 і
і
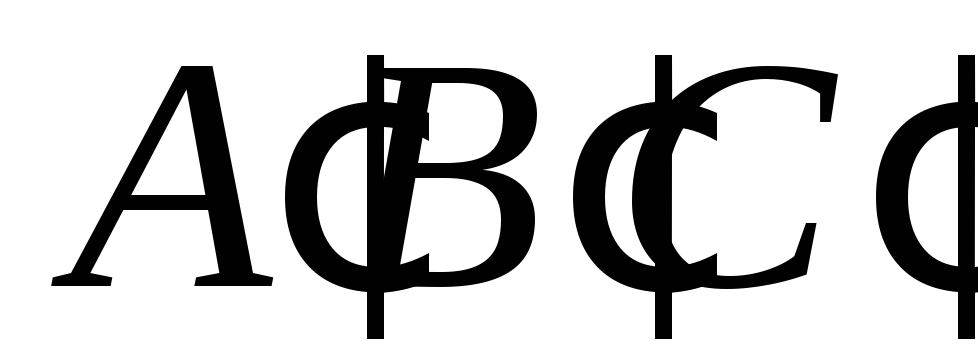 ,
пряму Дезарга
,
пряму Дезарга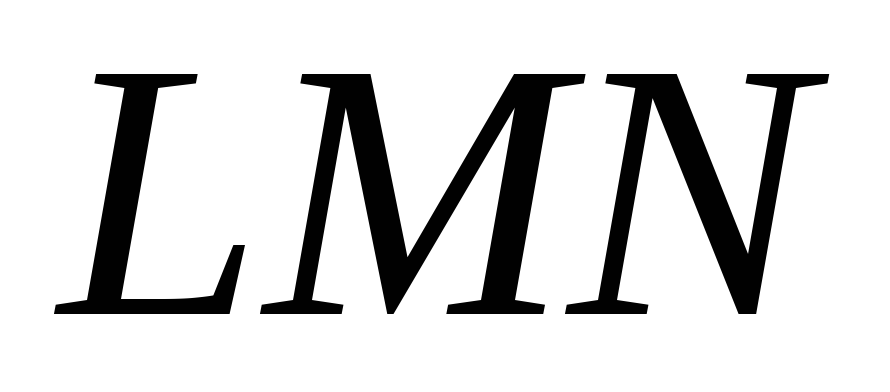 і точку Дезарга
і точку Дезарга
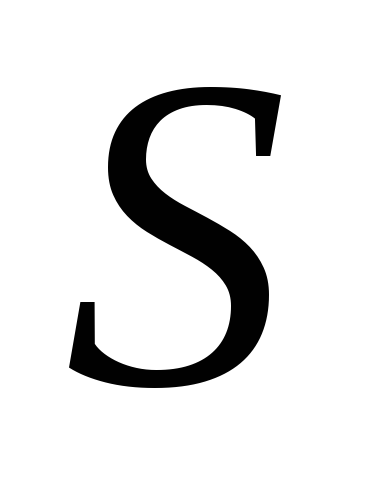 .
Прийнявши точку
.
Прийнявши точку
 за точку Дезарга, знайти для цього
випадку відповідні тривершинники і
пряму Дезарга.
за точку Дезарга, знайти для цього
випадку відповідні тривершинники і
пряму Дезарга.Точки
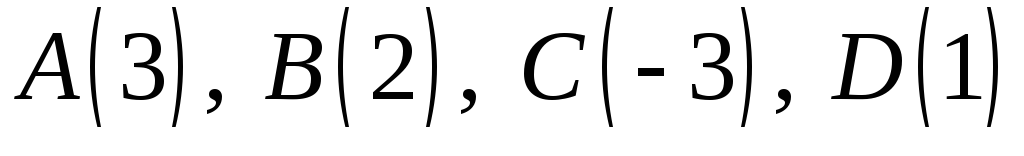 задано декартовими координатами на
прямій. Знайти значення всіх складних
відношень, які утворюються цими точками.
задано декартовими координатами на
прямій. Знайти значення всіх складних
відношень, які утворюються цими точками.Дано три прямі
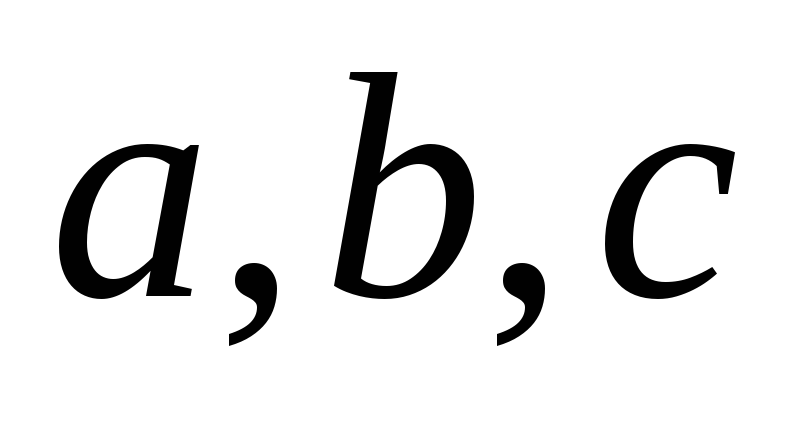 пучка
пучка із власним центром. Побудувати
четверту пряму
із власним центром. Побудувати
четверту пряму
 ,
гармонічно спряжену з прямою
,
гармонічно спряжену з прямою .
.На площині дано дві паралельні прямі
 і
і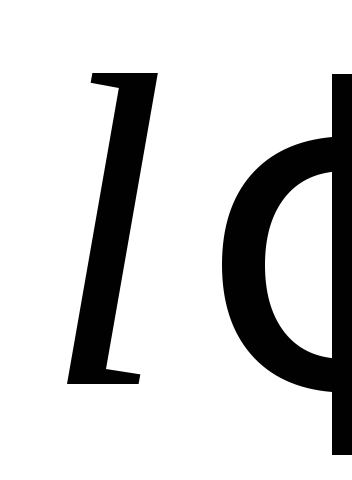 та відрізок
та відрізок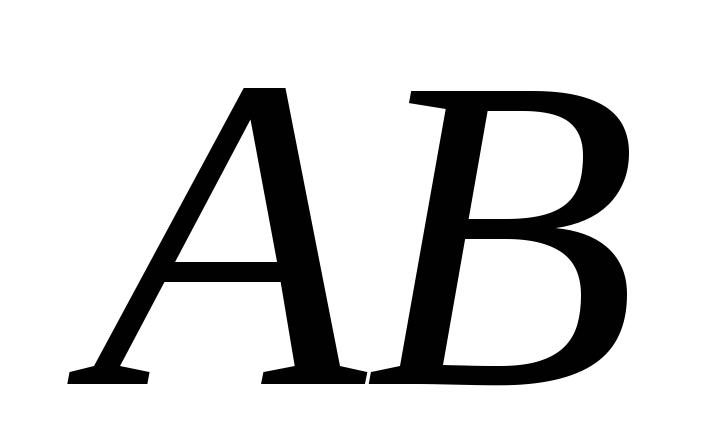 на прямій
на прямій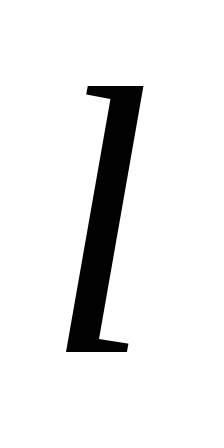 .
Використовуючи тільки односторонню
лінійку, подвоїти відрізок
.
Використовуючи тільки односторонню
лінійку, подвоїти відрізок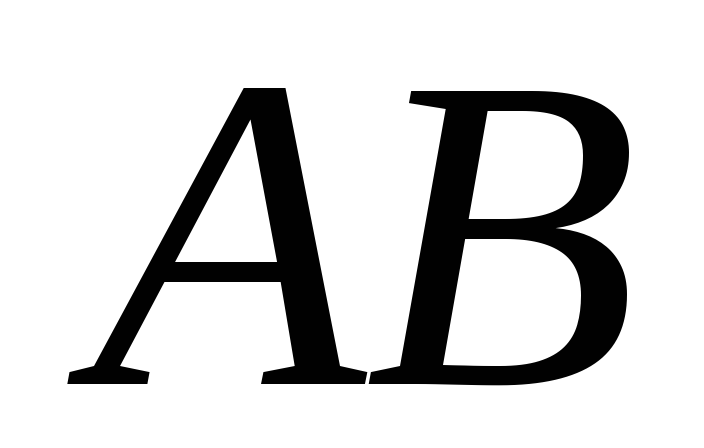 .
.Криву другого порядку задано п’ятьма точками
 .
За допомогою однієї лінійки побудувати
дотичну до кривої в точці
.
За допомогою однієї лінійки побудувати
дотичну до кривої в точці .
.Зробити рисунок до теореми Бріаншона для випадку, коли точка Бріаншона є невласною.
Дано (накреслено) криву другого порядку і точку
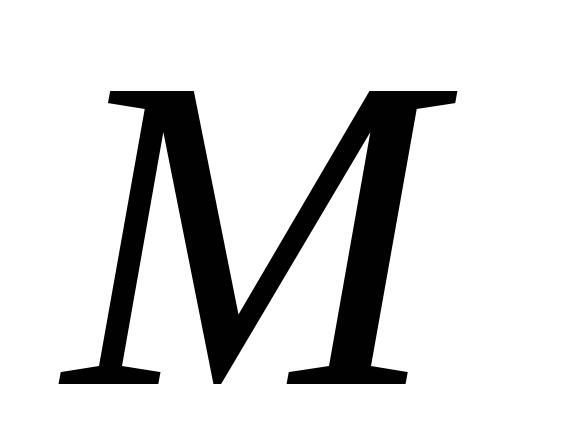 всередині кривої. Побудувати поляру
точки
всередині кривої. Побудувати поляру
точки відносно даної кривої.
відносно даної кривої.
