
- •Змістовий модуль 2 «Методи зображення просторових фігур на площині» Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 4
- •Варіант 5
- •Варіант 6
- •Варіант 7
- •Варіант 8
- •Варіант 9
- •Варіант 10
- •Змістовий модуль 3 «Елементи проективної геометрії» Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 4
- •Варіант 5
- •Варіант 6
- •Варіант 7
- •Варіант 8
- •Варіант 9
- •Варіант 10
ІНДИВІДУАЛЬНЕ ЗАВДАННЯ 2
Змістовий модуль 2 «Методи зображення просторових фігур на площині» Варіант 1
Побудувати зображення кола, описаного навколо правильного трикутника.
Побудувати зображення прямокутного паралелепіпеда, описаного навколо циліндра.
Побудувати переріз чотирикутної призми площиною
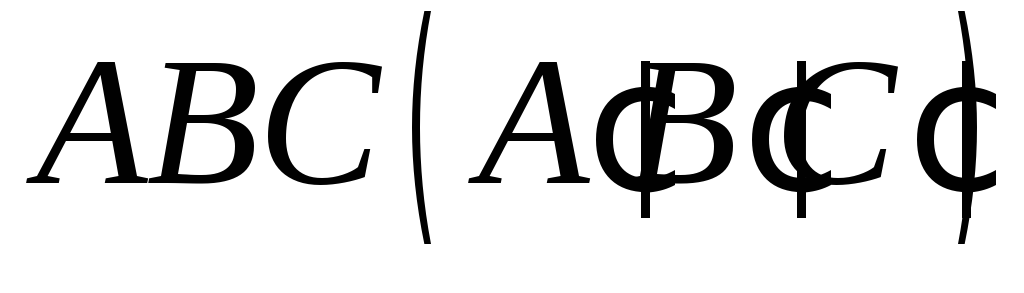 ,
якщо точка
,
якщо точка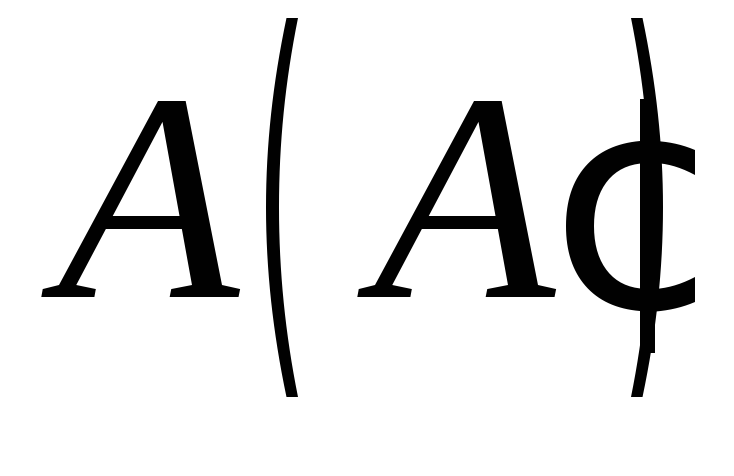 – вершина нижньої основи, точка
– вершина нижньої основи, точка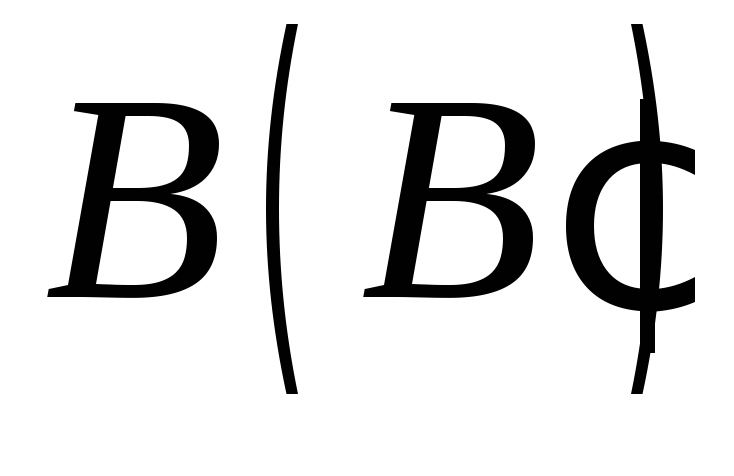 знаходиться на бічному ребрі, а точка
знаходиться на бічному ребрі, а точка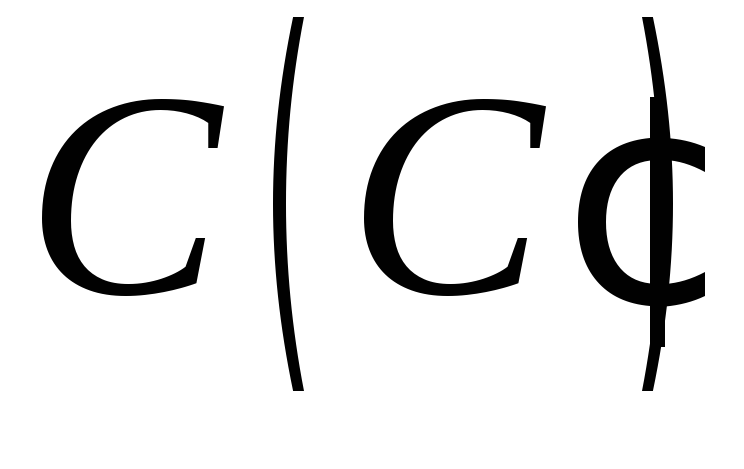 – всередині призми (методом внутрішнього
проектування).
– всередині призми (методом внутрішнього
проектування).Побудувати переріз п’ятикутної піраміди площиною
 ,
якщо точка
,
якщо точка знаходиться на стороні основи, а точки
знаходиться на стороні основи, а точки і
і – у суміжних бічних гранях (методом
слідів).
– у суміжних бічних гранях (методом
слідів).Дано зображення чотирикутної призми і прямої, яка перетинає дві суміжні грані призми. Знайти точки зустрічі цієї прямої з площинами всіх граней призми.
Побудувати переріз куба
 площиною, яка проходить через вершину
верхньої основи А і середини ребер BС
іC′D′.
площиною, яка проходить через вершину
верхньої основи А і середини ребер BС
іC′D′.Дано зображення правильної трикутної піраміди
 ,
бічні ребра якої втричі більші сторін
основи. Побудувати переріз піраміди
площиною, яка проходить через ребро
,
бічні ребра якої втричі більші сторін
основи. Побудувати переріз піраміди
площиною, яка проходить через ребро перпендикулярно до ребра
перпендикулярно до ребра .
.
Варіант 2
Побудувати зображення квадрата, вписаного в коло.
Побудувати зображення піраміди з ромбічною основою, описаної навколо конуса.
Побудувати переріз чотирикутної призми площиною
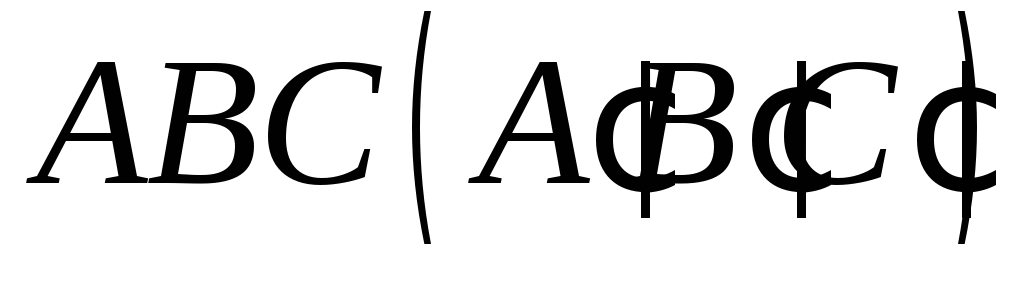 ,
якщо точки
,
якщо точки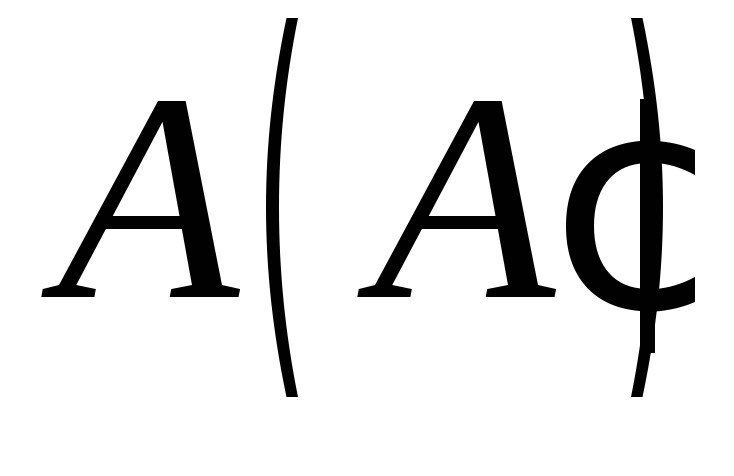 і
і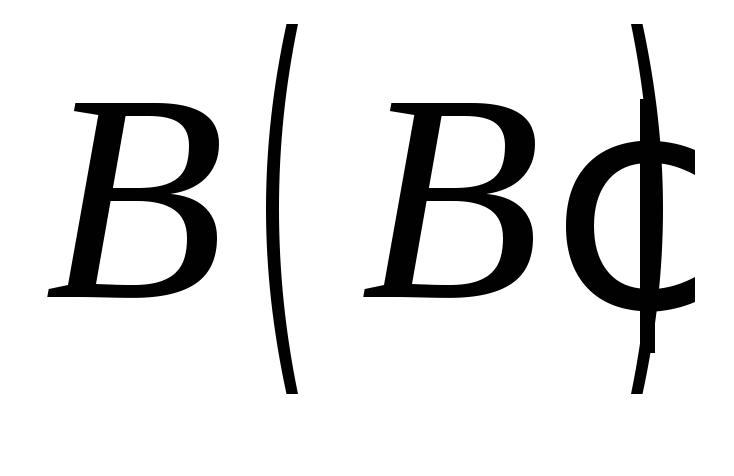 знаходяться на протилежних бічних
гранях, а точка
знаходяться на протилежних бічних
гранях, а точка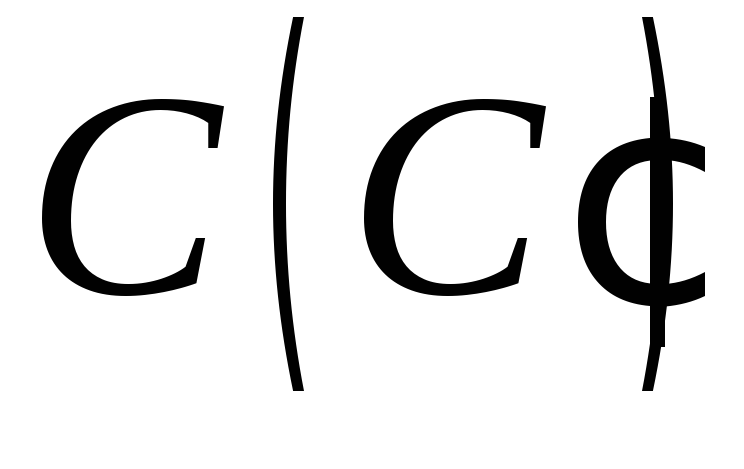 – поза призмою (методом слідів).
– поза призмою (методом слідів).Побудувати переріз п’ятикутної піраміди площиною
 ,
якщо точки
,
якщо точки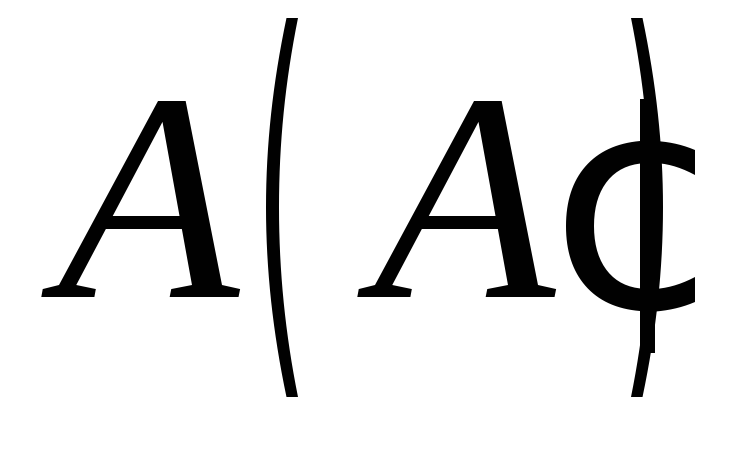 і
і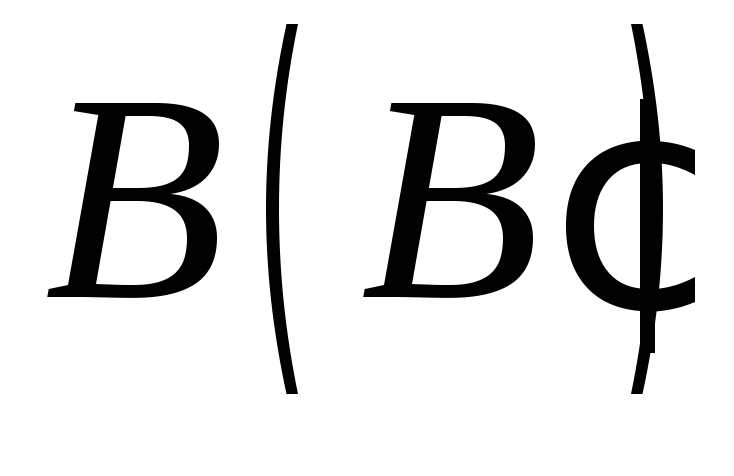 знаходяться на суміжних бічних ребрах,
а точка
знаходяться на суміжних бічних ребрах,
а точка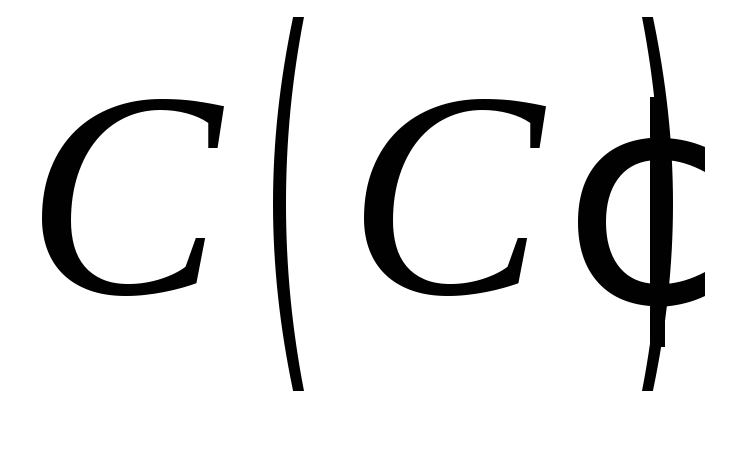 – всередині піраміди (методом
внутрішнього проектування).
– всередині піраміди (методом
внутрішнього проектування).Дано зображення чотирикутної призми та прямої, яка перетинає дві протилежні грані призми. Знайти точки перетину цієї прямої з площинами всіх граней призми.
Побудувати переріз куба
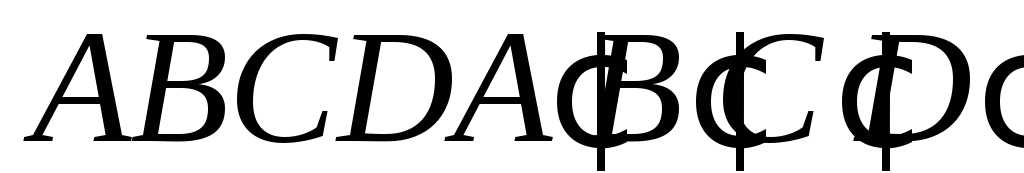 площиною, заданою трьома точками
на ребрах AA′, А′B′
іBC.
площиною, заданою трьома точками
на ребрах AA′, А′B′
іBC.Дано зображення правильного трикутника і другого трикутника, вершини якого розміщені довільно на сторонах першого. Побудувати зображення бісектриси і висоти одного з внутрішніх кутів другого трикутника.
Варіант 3
Побудувати зображення прямокутного трикутника, в якому один катет трикутника дорівнює половині іншого і з вершини прямого кута проведено медіану, бісектрису і висоту. Вказівка: обчислити відношення, в якому висота прямокутного трикутника ділить гіпотенузу.
Побудувати зображення описаної навколо конуса піраміди, основою якої є трапеція.
Побудувати переріз чотирикутної призми площиною
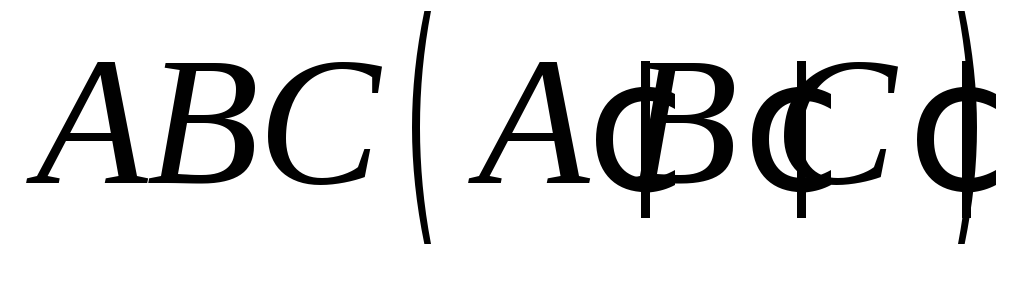 ,
якщо точка
,
якщо точка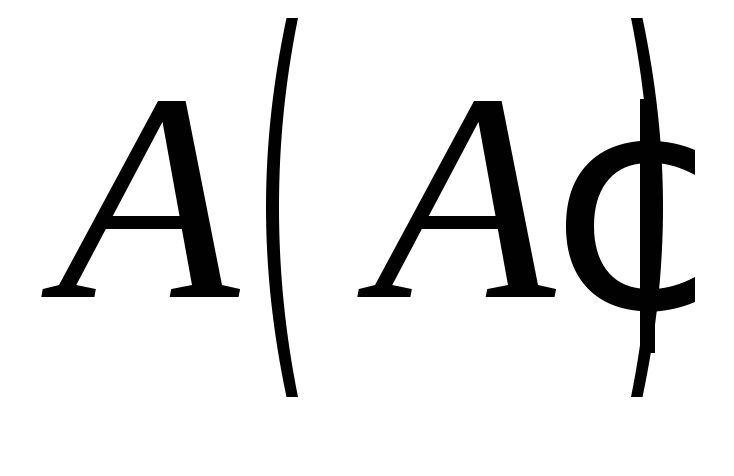 знаходиться на стороні верхньої основи,
точка
знаходиться на стороні верхньої основи,
точка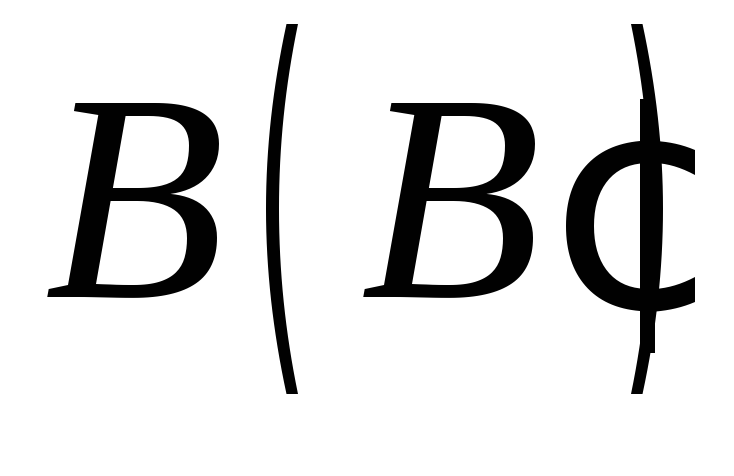 – на бічному ребрі, а точка
– на бічному ребрі, а точка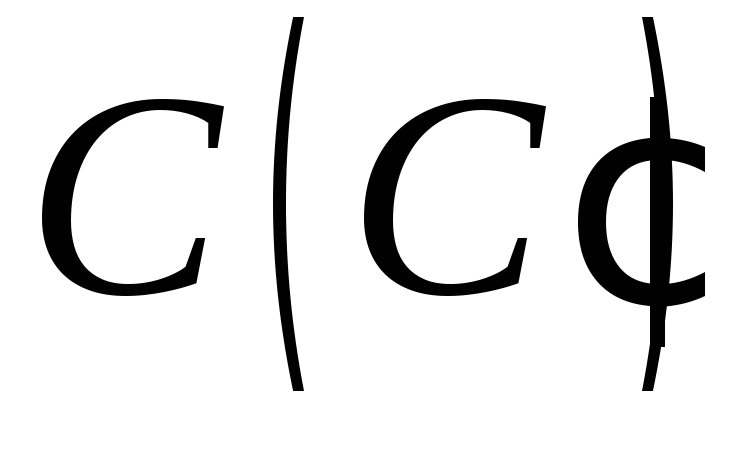 – всередині призми (методом внутрішнього
проектування).
– всередині призми (методом внутрішнього
проектування).Побудувати переріз п’ятикутної піраміди площиною
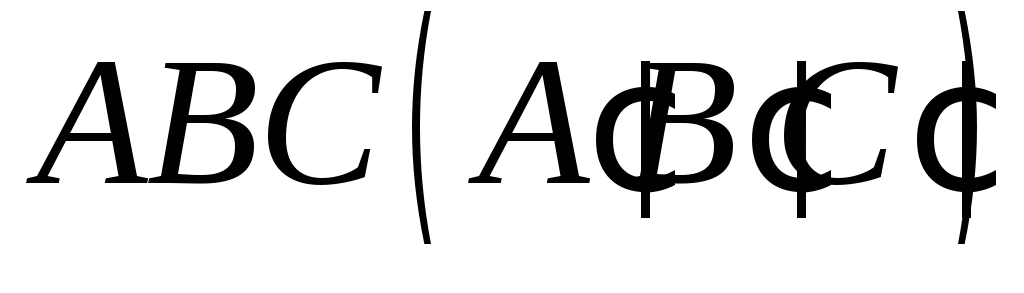 ,
якщо точки
,
якщо точки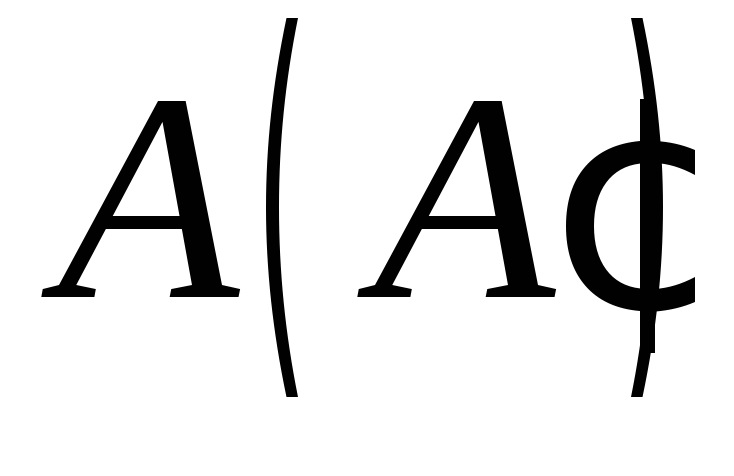 і
і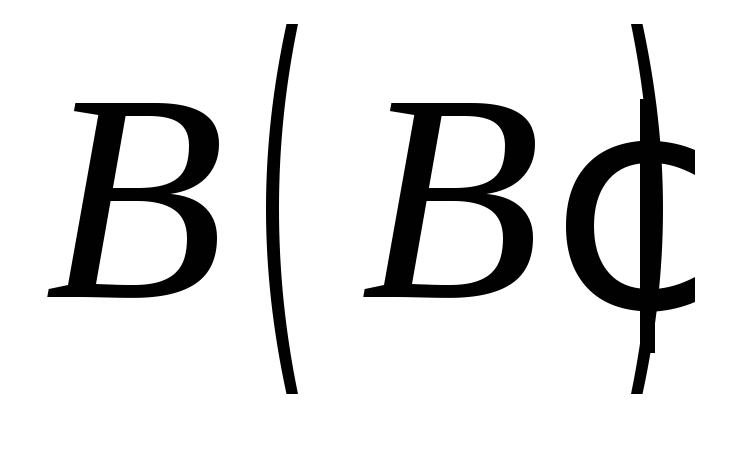 знаходяться на несуміжних бічних
ребрах, а точка
знаходяться на несуміжних бічних
ребрах, а точка – поза пірамідою (методом слідів).
– поза пірамідою (методом слідів).Дано чотирикутнику піраміду та пряму, яка перетинає дві протилежні бічні грані піраміди. Знайти точки перетину цієї прямої з площинами всіх граней піраміди.
Побудувати переріз куба
 площиною, яка проходить через середини
ребер ВС,C′D′
і CC′.
площиною, яка проходить через середини
ребер ВС,C′D′
і CC′.Дано зображення куба
 .
З точки
.
З точки грані
грані провести перпендикуляр до діагональної
площини
провести перпендикуляр до діагональної
площини .
.
