Точкова оцінка математичного сподівання

Нехай х₁, х₂, х₃, ..., х_n – вибірка отримана в результаті п незалежних випробувань над випадковою величиною Х – деякою ознакою генеральної сукупності, яка має математичне сподівання М(Х)=а.

За точкову оцінку математичного сподівання а =М(Х) беруть вибіркове середнє .

Легко довести, що є незміщеною для М(Х)=а, тобто М()=а.

Якщо додатково припустити, що випадкова величина Х має скінчену дисперсію , тоді можна стверджувати, що оцінкає змістовною. Якщо обчислити дисперсію вибіркової середньої, то отримаємо

.

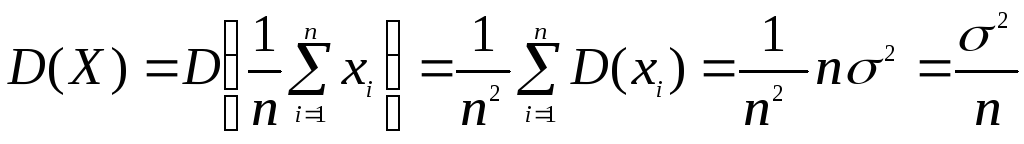Оскільки , то це означає, що оцінкає змістовною для параметраа.

Твердження. Якщо випадкова величина Х нормально розподілена з параметрами М(Х)=а і , то оцінкамає у класі всіх незміщених оцінок математичного сподівання а мінімальну дисперсію, яка дорівнює. Томує ефективною оцінкою параметра а.

Точкова оцінка дисперсії. Виправлена дисперсія

За точкову оцінку дисперсії беруть вибіркову дисперсію , яка є зміщеною оцінкою параметра . Цей факт випливає з рівності , яку неважко встановити за допомогою безпосередніх обчислень. Тому вибіркову дисперсію доцільно виправити таким чином, щоб вона стала незміщеною оцінкою. Для цього достатньопомножити на дріб.

Виправлену вибіркову дисперсію позначають .

Тоді виправленим середньоквадратичним відхиленням вибірки буде

Дріб називають поправкою Бесселя. Для малихп поправка Бесселя значно відрізняється від одиниці. Для п50 практично немає різниці між і.

Можна показати, що оцінки іє змістовними і не є ефективними.

У випадку, коли математичне сподівання а відоме і випадкова величина Х нормально розподілена, то незміщеною, змістовною та ефективною оцінкою дисперсії є оцінка

Точкові оцінки параметрів розподілу є випадковими величинами, їх можна вважати первинними результатами обробки вибірки тому, що невідомо, з якою точністю кожна з них оцінює відповідну числову характеристику генеральної сукупності.

Однак, при малому об’ємі вибірки точкові оцінки можуть мати значні розходження із значенням параметра, що оцінюється. Це призводить до грубих помилок.

Більш точними є інтервальні оцінки.

Означення. Інтервальною називають оцінку, яка визначається двома числами – кінцями інтервалу.

Інтервальні оцінки дозволяють встановити точність та надійність оцінок.

Нехай за даними вибірки знайдена статистична оцінка невідомого параметра, який бдемо вважати сталим числом. Очевидно, щотим точніше визначає параметр, чим менша за абсолютною величиною різниця.

Означення. Число δ, для якого виконується нерівність <δ, називають точністю оцінки.

Означення. Надійністю оцінки по називають ймовірністьγ, з якою виконується нерівність< δ або

γ=Р(<δ) (20)

Найчастіше число γ задається наперед і, залежно від обставин дорівнює 0,95 або 0,99, або 0,999.

Замінимо нерівність на рівносильну.

Звідси формулу (20) можна переписати у такому вигляді

.

Означення. Інтервалом довір’я або довірчим інтервалом називають інтервал , який із заданою надійністюпокриває невідомий параметр.

Зауваження. Кінці довірчого інтервалу є випадковими величинами.