6.1.2. Неперервні випадкові величини. Щільність розподілу.

Як уже згадувалось в розділі 6.1, під неперервною випадковою величиною слід розуміти випадкову величину, яка може приймати будь-яке числове значення з деякого скінченого або нескінченного інтервалу (а;в).

Головна різниця в задачах обчислення ймовірностей для дискретних і неперервних випадків полягає в тому, що в дискретному випадку шукається ймовірність типу Х=с (випадкова величина прийме конкретне значення), а у випадку неперервної величини ймовірність такого типу дорівнює нулю, тому для її повної характеристики водять поняття інтегральної та диференціальної функції розподілу, а цікавими для нас є ймовірності подій типу аХв (випадкова величина прийме значення з деякого проміжку). При цьому:

р(аХв)= р(аХв)= р(аХв)= р(аХв)

Означення. Інтегральною функцією розподілу випадкової величини Х називають функцію F(X), яка визначає ймовірність того, що випадкова величина Х прийме значення менші х ( х R), тобто

F(X) = P(X < x) (16)

Властивості інтегральної функції розподілу

1. 0≤ F(X) ≤1.

2. Функція розподілу є неспадною: якщо х₁<х₂, то F(х₁) < F(х₂).

3. Ймовірність попадання випадкової величини Х в інтервал (а;в) <.

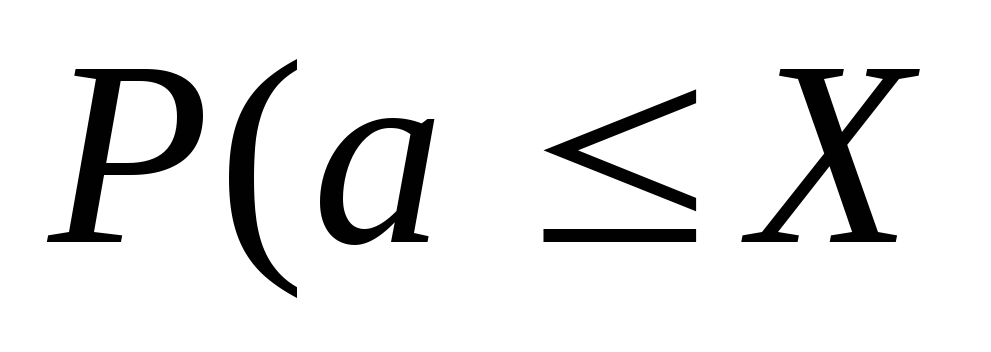4. Функція розподілу неперервна зліва: .

5. або <.

6. ; .

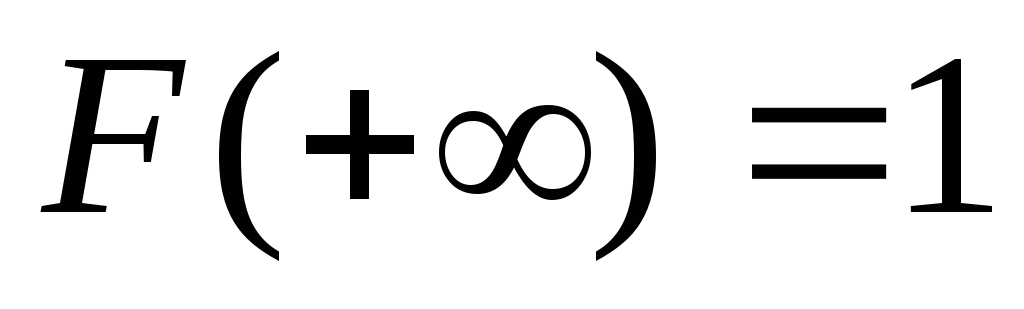Має місце факт: ймовірність події аХв рівна площі фігури, обмеженої прямими у=0, х=а, х=в і графіком функції . Тобто справедлива рівність

р(аХв)=, для будь-якиха і в, ав.

Ця рівність виконується і для загального випадку, якщо невід’ємна.

Таким чином, функція дозволяє обчислити ймовірності, пов’язані з випадковою величиною Х, тобто задає закон розподілу НВВ Х, а функціюназиваютьдиференціальною функцією розподілу або щільністю ймовірностей.

Якщо F(x) диференційована і похідна її обмежена, то випадкова величина Х, має щільність розподілу ймовірностей .

Графік функції називають кривою розподілу неперервної випадкової величини. Він може мати вигляд, зображений на рис. 4.

Властивості диференціальної функції розподілу

1. для всіх .

2. .

3. , при ха та хв.

Теорема

Ймовірність того, що НВВ Х прийме значення з інтервалу (а;b), можна знайти за формулою

.

Задача 4. Нехай НВВ Х задана щільністю ймовірностей розподілу

.

Знайти ймовірність того, що Х прийме значення на відрізку [0;1].

Розв’язання. .

Відповідь: 0,25.

Основні закони розподілу неперервних величин

Основні закони розподілу неперервних величин розрізняють за виглядом їх диференціальних функцій розподілу, тобто щільності ймовірностей .

1. Рівномірний розподіл

Величина Х розподілена рівномірно на проміжку (а;b), якщо усі її можливі значення належать цьому проміжку, а щільність її ймовірностей у цьому проміжку постійна, тобто

.

Якщо Х розподілена рівномірно на проміжку (а;b), то ймовірність належності Х будь-якому інтервалу (х₁;х₂)(а;b) пропорційна довжині цього інтервалу:

(х₁<Х<х₂)=, (a<Х<b)=1.

Цьому закону розподілу підлягають похибки округлення різноманітних розрахунків.

Графік щільності рівномірного розподілу має вигляд рис. 5.

2. Показниковий розподіл

Випадкову величину Х називають розподілену за показниковим законом розподілу, якщо щільність її ймовірностей має вигляд

, де >0.

Показниковому розподілу задовольняють: час телефонної розмови, час безвідмовної роботи годинника.

Графік щільності показникового розподілу має вигляд рис. 6.

3. Нормальний розподіл

Випадкову величину Х називають розподіленою нормально, якщо щільність її ймовірностей має вигляд

, де а і – параметри розподілу.

Графік щільності нормального розподілу називають кривою Гауса і зображають рис. 7.

1) точки та– точки перегину.

2) max в точці,.

Для неперервних випадкових величин також можна розглядати числові характеристики. Вони обчислюються за допомогою щільності розподілу.