Добавил:

Sergo Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Государственный университет управления

Предмет:

Высшая математика

Файл:

Учебник 1 курс 2 семестр.pdf

Скачиваний:

Добавлен:

16.12.2013

Размер:

1.39 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

				−	5	sin x
y				−	8	sin x
y		=							.
		=	1				1		.
z			1	cos x		−	1
	2		8	cos x		−	2	sin x
			8				2

Вопросы и упражнения для самостоятельной работы

1.От какого количества независимых параметров зависит общее решение системы линейных дифференциальных уравнений с постоянными коэффициентами, содержащей 4 уравнения?

2.Как связаны общие решения неоднородной и соответствующей однородной систем линейных дифференциальных уравнений? Приведите примеры.

3.Решить системы методом подстановки:

а)	y′= z +1,	б)	y′ = y + z,
а)		б)
	z′= y +1,		z′ = 3z −2 y.

4.Решитьоднородные системы методомматричного представления

а)	y′ = y −3z,	б)	y′ = 2 y + z,
а)		б)
	z′ = 3y + z,		z′ = 4z − y,

в)

г)

д)

x′ = 4 y −2z −3x,
	( λ =1;2; −1)
y′ = z + x,

z′ = 6x −6 y +5z,
x′ = x − y − z,
	( λ =1;1 ± 2i )
y′ = x + y,

z′ = 3x + z,
x′ = 3x −2 y − z,
	−3z, ( λ = 2; 2; −5 )
y′ = 3x −4 y

z′ = 2x −4 y.

5.Дайте определение собственных и присоединенных векторов системы. В каких случаях применяют метод присоединенных векторов?

6*. Решитьоднороднуюсистемуметодомприсоединенныхвекторов

x′ = 2x + y,y′ = 2 y + 4z,

z′ = x − z.

7.Решить неоднородные системы, используя матричное представление

а)

′

= 3y + 2z + 4e

б)

y′ = z −5cos x,

z′ = y + 2z.

z′ = 2 y + z.

′ = 2 y + z + 2e

в)

′

4 x

= y + 2z −3e

§ 7. Дифференциальные уравнения в частных производных. Основные понятия

Дифференциальным уравнением в частных производных называется дифференциальное уравне-

ние, в котором неизвестная функция является функцией нескольких переменных (двух и более). Общим решением дифференциального уравнения в частных производных называется все множе-

ство его решений (или такая запись ответа, которая включает в себя каждое частное решение).

= ex − y .

Важным отличием уравнений с частными производными от обыкновенных дифференциальных уравнений является зависимость общего решения не от произвольных констант C1,C2 ,...,Cn , а от не-

которого семейства произвольных функций ϕ1,ϕ2 ,K,ϕn , причем их количество n совпадает с по-

рядком дифференциального уравнения в частных производных, т.е. совпадает с максимальным порядком частных производных, входящих в уравнение.

П ри ме р ы

1.Найти общее решение уравнения в частных производных первого порядка

∂z(x, y) = 2x + y2 .

∂x

Ре ш е н и е . Проинтегрируем данное уравнение по x , считая переменную y произвольно

фиксированной:		dx = ∫(2x + y2 )dx
∫	∂z(x, y)		z(x, y) = x2 + y2 x +C( y) .

	∂x

Обратим внимание на то, что постоянная интегрирования C не зависит от переменной интегрирования x , но зависит от оставшейся переменной y , по которой интегрирование не проводилось. Пере-

обозначим C( y) = ϕ( y) и запишем ответ:

z(x, y) = x2 + y2 x + ϕ( y) .

Здесь записано общее решение, зависящее от произвольной функции ϕ( y) . Любые частные решения данного уравнения можно получить путем конкретного выбора функции ϕ( y) , например, функция z(x, y) = x2 + y2 x + 2 − e5 y +sin y является частным решением, т.к. соответствует выбору

ϕ( y) = 2 − e5 y +sin y .

2. Найти какое-либо частное решение уравнения в частных производных второго порядка

∂2 z(x, y)

∂x∂y

Ре ш е н и е . Найдем общее решение данного уравнения. Проинтегрируем его сначала по x :

∫

∂2 z(x, y)

dx = ∫(ex

− y)dx , откуда

∂z(x, y)

= ex − yx +C1( y) . Затем еще раз проинтегрируем, но уже

∂x∂y

∂y

по y : ∫

∂z(x, y)

dy = ∫(ex − yx +C1( y))dy , следовательно,

∂y

z(x, y) = yex −

xy2

+ ∫C1( y)dy +C2 (x) .

Для удобства введем следующие переобозначения:

∫C1( y)dy = ϕ1( y) , а C2 (x) = ϕ2 (x) , тогда

общее решение уравнения записывается в виде

z(x, y) = yex −

xy2

+ ϕ ( y) +ϕ

(x) ,

где ϕ1( y) и ϕ2 (x)

– две произвольные функции. (Заметим, что количество произвольных функций

совпадает с порядком уравнения.) Выберем из полученного общего решения произвольное частное решение: ϕ1( y) = y, ϕ2 (x) = 0 , откуда

z(x, y) = yex − xy22 + y .

∑Замена переменных.

Дифференциальные уравнения в частных производных можно пытаться решить путем введения новых переменных или замены неизвестной функции.

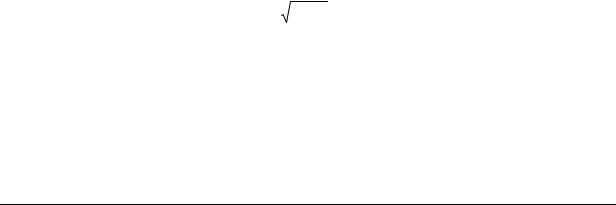
3.Решить дифференциальное уравнение в частных производных первого порядка zx + zy = 2 ,

u = x + y

с помощью замены переменных v = x − y .

Ре ш е н и е . Выразим частные производные zx и zy, входящие в уравнение, через частные про-

изводные по новым переменным zu	и zv :	zx = zuux + zvvx	zx = zu + zv	. Здесь мы воспользова-
изводные по новым переменным zu	и zv :			. Здесь мы воспользова-
		zy = zuuy + zvvy	zy = zu − zv

лись правилом вычисления производной сложной функции нескольких переменных. После подстановки в исходное уравнение получим новое уравнение zu =1 , которое легко интегрируется:

z(u,v) = u + ϕ(v) или, в старых переменных, z(x,y) = x + y + ϕ(x – y) , где ϕ(x – y) – произвольная функция от x – y.

Вопросы и упражнения для самостоятельной работы

1.В чем принципиальное отличие структуры общего решения для обыкновенных дифференциальных уравнений и уравнений в частных производных? Ответ поясните примерами.

2.Почему константа интегрирования C , возникающая при решении уравнений в частных производных, "на самом деле" не является постоянной величиной?

7*.

Найти общее решение уравнения zy = x		1 + y2 и указать несколько частных решений.
Найти общее решение уравнения zx – 2z = yx.
Спомощьюподходящейзаменыпеременныхрешитьуравнение
а) zx + zy = sin(x + y),	б) zx + zy = sin(x − y).
	u = xy,		решить уравнение	xzx − yzy = x2 y − xy2 .
Используя замену переменных
	v = x + y,

Найти общее решение уравнения zyy –2zy + z = x.

§ 8. Линейные уравнения в частных производных первого порядка

Дифференциальное уравнение в частных производных вида

∂z

+ a

∂z

+K+ a

∂z

= f ,

(1)

2 ∂x

n ∂x

1 ∂x

где ak = ak (x1, x2 ,K, xn ; z)

– заданные функции ( k =

f = f (x1, x2 ,K, xn ; z) – заданная правая

1, n

часть (неоднородность), а z = z(x1, x2 ,K, xn ) – неизвестная функция, называемая линейным неодно-

родным или квазилинейным уравнением первого порядка в частных производных.

Решение уравнений в частных производных вида (1) сводится к нахождению первых интегралов некоторой системы обыкновенных дифференциальных уравнений, называемой характеристической системой.

Первым интегралом системы обыкновенных дифференциальных уравнений называется такая величина ϕ, зависящая от переменной и неизвестных функций, которая не изменяется на решении,

т.е. если вместо функций подставить решение системы, то данная величина будет константой. Поясним это определение простейшим примером. Пусть решение некоторого уравнения имеет

вид y(x) = x +C , где C – произвольная постоянная. Тогда величина ϕ = y − x = C сохраняется на решении, следовательно, является первым интегралом.

Метод характеристик

	Для решения линейного уравнения в частных производных первого порядка необходимо:
	1. Составить				характеристическую систему обыкновенных дифференциальных уравнений
dx1	= dx2		=K= dxn		= dz ;
a	a	2	a	n	f
1

2. Найти n независимых первых интегралов:

ϕ1(x1,...xn ; z) = C1, ϕ2 (x1,...xn ; z) = C2 ,

ϕn (x1,...xn ; z) = Cn .

3. Записать общее решение в неявном виде F(ϕ1, ϕ2 ,..., ϕn ) = 0 , где F – произвольная функция.

З а м е ч а н и е . Если функция z присутствует только в одном из первых интегралов (например, в последнем), то решение можно записать в виде

ϕn (x1,..., xn ; z) = F(ϕ1, ϕ2 ,.., ϕn −1 ) ,

если при этом удается выразить z , то общее решение можно записать в явном виде.

П ри ме р ы

1. Найти общее решение линейного уравнения первого порядка в частных производных zx + zy = 2 (пример 3 §7).

Ре ш е н и е . Составим характеристическую

систему

дифференциальных

уравнений

dx = dy

согласно пункту 1. Запишем эту систему в эквивалентном виде

dz . Переменные

dy =

в обоих уравнениях разделены, и после интегрирования каждого получаем:

= y +C

. Следова-

2 y = z +C2

тельно, независимые первые интегралы принимают вид:

− y = C

. Общее решение z(x, y)

можно

2 y − z = C2

записать, используя неявное представление, следующим образом:

F(x − y, 2 y − z) = 0 , где F

– про-

извольная функция. Однако вид полученных первых интегралов позволяет записать решение явно, а

именно: искомая функция		z входит только в последний из первых интегралов, следовательно, по-
лучаем	(см. замечание)	2 y − z = F(x − y)	или	z(x, y) = 2 y − F(x − y) .	Переобозначим
F(x − y) = −ϕ(x − y) и получим окончательный ответ:
		z(x, y) = 2 y +ϕ(x − y) ,
где ϕ(x − y) – произвольная функция.
В	предыдущем параграфе мы получили,			на первый взгляд,	другой ответ:

z(x, y) = x + y +ϕ(x − y) . Мы предлагаем вам самостоятельно убедиться в том, что ответы полностью

совпадают (различие состоит лишь в форме записи).
2. Найти общее решение линейного уравнения первого порядка					в частных производных
(x + 2 y) zx − y zy = 0 и указать какие-либо его частные решения.
Ре ш е н и е . Характеристическая система имеет вид
	dx	=	dy	= dz .
	x + 2 y	=	− y	= dz .
	x + 2 y		− y	0
Формальное деление на ноль приводит к dz = 0 . Запишем первое уравнение:						dx	=	dy	или в
						x + 2 y	=		или в
						x + 2 y		− y
приведенном виде − ydx = (x + 2 y)dy , следовательно,				xdy + ydx + 2 ydy = 0	d (xy) + d ( y2 ) = 0 , и

после интегрирования получаем один из первых интегралов xy + y2 = C1 . Рассмотрим второе уравнение в системе dz = 0 , откуда z = C2 – еще один первый интеграл. Общее решение записываем в яв-

ном виде z(x, y) = ϕ(xy + y2 ) . Частные решения получим произвольным выбором функции ϕ: для ϕ(u) = cosu получим частное решение

z(x, y) = cos(xy + y2 ) ,

для ϕ(u) = ln u −3 u получим соответственно

z(x, y) = ln(xy + y2 ) −3 xy + y2 .

3.Найти общее решение уравнения

∂z

+ yz

∂z

= xy .

∂x

∂y

Ре ш е н и е . Записываем вспомогательную систему:

= dy = dz

. Первое уравнение приво-

дит к следующим преобразованиям:

= dy

∫ dx

= ∫

x = C1 y ϕ1

= C1 является

одним из первых интегралов.

dy = dz

или dy = dz

Следующее уравнение:

. Мы видим, что в это уравнение входит "лишняя"

переменная x . Выразим ее через найденный первый интеграл x =C y

dy =

C ydy = zdz ,

C1 y

после интегрирования и сокращений получаем

C y2 = z2 +C

. Для того,

чтобы окончательно выпи-

сать еще один первый интеграл ϕ

= C

, необходимо обратно заменить C на выражение C =

. В

итоге имеем: ϕ2 = xy − z2 = C2 . Функция z

входит только в ϕ2 ,

следовательно, запишем общее ре-

шение в явном виде: xy − z

= F

z = ±

xy − F

. Окончательный ответ принято макси-

мально упрощать с помощью переобозначений произвольных функций, т.е.

z = ±

xy +ϕ

4*. Найти общее решение уравнения

(x + z)zx +( y + z)zy = x + y .

Ре ш е н и е . Выпишем вспомогательную систему:

. Особенность данной

x + z

y + z

x + y

системы дифференциальных уравнений заключается в том, что ни одно из ее уравнений не удается проинтегрировать сразу, т.к. переменные оказываются не разделены. Если бы нам был известен один первый интеграл ϕ1(x, y; z) = C1 , то можно было бы выразить одну переменную через другие и под-

ставить в уравнение системы (пример 3), однако мы не знаем ни одного первого интеграла.

В этом случае необходимо тождественно преобразовать систему к интегрируемому виду, ис-

пользуя следующее свойство

обыкновенных

дробей: если

a1 = a2

=K= an

, то для любых

k1, k2 ,..., kn выполняется

= a2

=K= an

k1a1 + k2a2 +... + knan

(докажите).

k b + k

+... + k

1 1

2 2

n n

В нашем случае можно сделать следующее. Пусть сначала все ki

=1 , тогда получим

1dx +1dy +1dz

x + z

y + z

x + y

1(x + z) +1( y + z) +1(x + y)

или после упрощений

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
16.12.201348.13 Кб27vyshka_var_2008.doc
#
16.12.201365.54 Кб73Билет по высшей математике.doc
#
16.12.2013498.16 Кб26Билет по вышке 2 семестр 2005-2006.jpg
#
16.12.2013385.09 Кб53Билеты по высшей математике ГУУ.jpg
#
16.12.201327.14 Кб144Высшая математика. Экзаменационный билет за 2-й се.doc
#
16.12.20131.39 Mб91Учебник 1 курс 2 семестр.pdf