
- •1. Фізичні основи класичної механіки Основні формули Елементи кінематики
- •Елементи динаміки
- •Приклади розв’язання задач.
- •Тема № 2. Молекулярна фізика та термодинаміка. Основні формули
- •Окремі випадки розподілу Гіббса:
- •Приклади розв’язання задач Приклад 1. Знайти густину кисню при нормальних умовах.
- •Тема №3 електростатика. Електричний струм. Основні формули
- •Приклади розв’язання задач.
- •Тема № 4 електромагнетизм Основні формули
- •Коливання та хвилі Основні формули
- •Приклади розв’язання задач
- •Тема №5
- •Основні формули
- •Фотометрія
- •Геометрична оптика
- •Хвильова оптика
- •Елементи релятивістської динаміки
- •Квантова теорія випромінювання. Фотони.
- •Приклади розв’язання задач
Приклади розв’язання задач
Приклад 1. Знайти індукцію магнітного поля у точці, яка розташована на відстані R=5см від тонкого нескінченного провідника, через який тече струм I=2A.
Розв’язання
С користаємось
законом Біо-Савара-Лапласа, щоб отримати
формулу для розрахунку магнітної
індукції в точці М. Виділимо на провіднику
елемент dl, який розташований на відстані
l від точки О і на відстані r від точки
М. Це елемент утворює в точці М індукцією
користаємось
законом Біо-Савара-Лапласа, щоб отримати
формулу для розрахунку магнітної
індукції в точці М. Виділимо на провіднику
елемент dl, який розташований на відстані
l від точки О і на відстані r від точки
М. Це елемент утворює в точці М індукцією
![]() ,
яка згідно з (4.2) напрямлена перпендикулярно
до площини рисунка за рисунок і
,
яка згідно з (4.2) напрямлена перпендикулярно
до площини рисунка за рисунок і
Рис. 4.2. згідно з (4.3) має величину
dB=![]() dl
(1)
dl
(1)
Повна індукція
![]() (2)
(2)
Поділимо провідник на дві рівні частини (при цьому інтеграл треба подвоїти) і виразимо змінні l і r через кут α. З рисунка випливає
![]()
![]()
![]()
![]() .
.
Підставимо dl і r в (2):
 (3)
(3)
Перевіримо одиницю вимірювання
![]()
Виразимо величини в одиницях Сі і підставимо в (3):
![]()
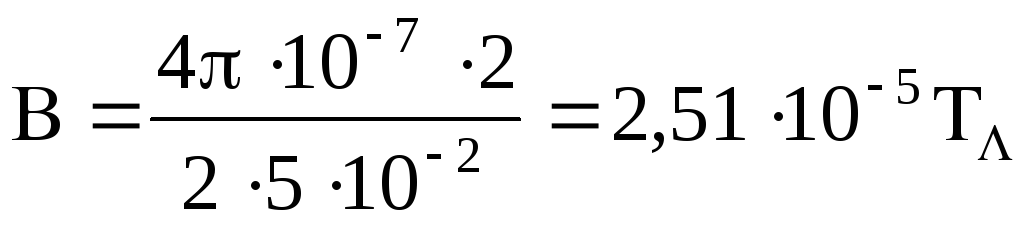 =0,25мкТл
=0,25мкТл
Відповідь: В=0,25мкТл.
Приклад 2. Два прямолінійних нескінченних провідника розташовані паралельно на відстані
l
=10см один від одного. По провідникам
протікають однакові струми
![]() у протилежних напрямках. Знайти індукцію
магнітного поля у точці, яка віддалена
від кожного провідника на відстань
у протилежних напрямках. Знайти індукцію
магнітного поля у точці, яка віддалена
від кожного провідника на відстань![]() .
.
![]()
 Розв’язання.
Розв’язання.
Нехай
провідники розташовані
перпендикулярно до площини рисунку.
Точка М і провідники утворюють
рівносторонній трикутник зі стороною
10 см. Тому
![]() .
Згідно з формулою (3)
з
приклада
.
Згідно з формулою (3)
з
приклада
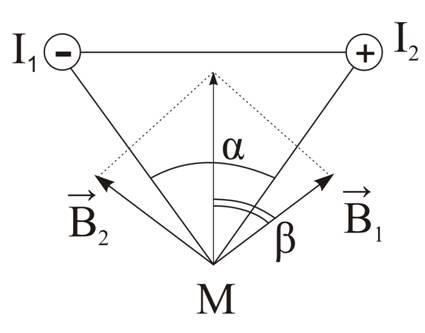
1 індукції В1 і В2, які утворюють струми
І1 і І2, можна визначити за формулою
Рис.
4.3.
![]() .
.
За
принципом суперпозиції
![]() .
.
Напрямки
![]() ,
,![]() і
і![]() показані на рис. 4.3. З рисунку випливає,
то кут β теж дорівнює 600.
Це означає, що вектори
показані на рис. 4.3. З рисунку випливає,
то кут β теж дорівнює 600.
Це означає, що вектори
![]() ,
,![]() і
і![]() теж утворюють рівносторонній трикутник,
тому
теж утворюють рівносторонній трикутник,
тому
B = B1 =B2.
Підставимо числові данні, вважаючи, що μ =1.

Відповідь: В = 12,6 мкТл.
Приклад
3.
Знайти індукцію магнітного поля
усередині соленоїда довжиною l=
25см, який має N=500
витків. Сила струму, який протікає через
соленоїд,
![]() .
Діаметр соленоїда вважати набагато
меншим за його довжину. Осередь –
повітря.
.
Діаметр соленоїда вважати набагато
меншим за його довжину. Осередь –
повітря.
Розв’язання.
 За
допомогою теореми про циркуляцію
напруженості магнітного поля знайдемо
формулу для розрахунку напруженості.
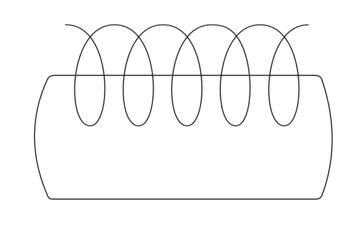
Магнітне поле існує тільки у серед
соленоїда. Виберемо замкнутий контур
так, щоб його частина проходила через
внутрішній простір соленоїда. Цей контур
охоплює Ν витків. Тоді за формулою (4.4)
За
допомогою теореми про циркуляцію
напруженості магнітного поля знайдемо
формулу для розрахунку напруженості.
Магнітне поле існує тільки у серед
соленоїда. Виберемо замкнутий контур
так, щоб його частина проходила через
внутрішній простір соленоїда. Цей контур
охоплює Ν витків. Тоді за формулою (4.4)
Рис.
4.4.
![]() ,
,
звідки
![]() ,
і згідно з (4.1)
,
і згідно з (4.1)![]() .
.
Перевіримо одиницю вимірювання
![]() .
.
Підставимо числові дані
 .
.
Відповідь:
![]() .
.
Приклад
4.
Два провідника розташовані паралельно
у повітрі на відстані =50см один від
одного. Через провідники у однаковому
напрямку проходять струми
![]() .
Визначити силу взаємодії, яка припадає
на одиницю довжини кожного провідника.
Притягуватися чи відштовхуватися будуть
провідники?
.
Визначити силу взаємодії, яка припадає
на одиницю довжини кожного провідника.
Притягуватися чи відштовхуватися будуть
провідники?
Розв’язання.
 Будемо
вважати, що провідник зі струмом
Будемо
вважати, що провідник зі струмом
![]() знаходиться
у магнітному полі, яке створює струм
знаходиться
у магнітному полі, яке створює струм![]() .
Індукція цього поля (приклад 1):
.
Індукція цього поля (приклад 1):
![]() .
.
Тоді
на елемент dl
струму
![]() діє сила (4.6)
діє сила (4.6)
![]() ,
,
Рис.
4.5. або
![]() .
.
У нашому випадку α = 900, μ = 1, тому на одиницю довжини припадає сила
![]()
Перевіримо одиницю вимірювання.
![]() .
.
Підставимо числові значення

 .
.
Н
F
Відповідь: F = 1,26 Н/м ; притягуються.
Рис. 4.6.
Приклад 5. Протон, який пройшов прискорюючи різницю потенціалів U = 500 B, влетів у однорідне магнітне поле перпендикулярно лініям магнітної індукції. Визначити радіус траєкторії протона. Індукція магнітного поля В=0,5 Тл.
Розв’язання.
На
протон діє сила Лоренца (4.10). Оскільки
кут між швидкістю
![]() і індукцією
і індукцією![]() дорівнює 900
дорівнює 900
![]() ,
то сила Лоренца є доцентровою і змушує
протон рухатись по колу. Згідно з другим
законом Ньютона
,
то сила Лоренца є доцентровою і змушує
протон рухатись по колу. Згідно з другим
законом Ньютона
![]() ,
,
або
![]() ,
,
звідки
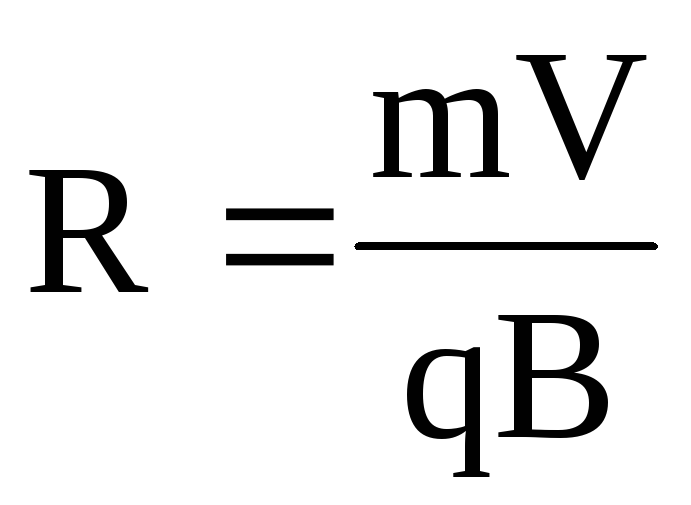 ,
(1)
,
(1)
де
![]() кг
– маса
протона, q=1,6∙
кг
– маса
протона, q=1,6∙![]() Кл
– заряд протона.
Кл
– заряд протона.
Швидкість
v
знайдемо, скориставшись зв`язком між
роботою електричного поля по переміщенню
протона зі зміною його кінетичної
енергії
![]() .
.
Вважаючи початкову швидкість протона рівною нулю, маємо
![]() ,
звідки
,
звідки
 (2)
(2)
Підставимо (2) у (1) і отримаємо
 .
(3)
.
(3)
Перевіримо одиницю вимірювання

Підставимо в (3) числові дані

Відповідь:
![]() .
.
Приклад
6.
Повна енергія гармонічних коливань
матеріальної точки
![]() ;
максимальна сила, яка діє на точкуFmax=2мН.
Записати рівняння цих коливань, якщо
період
;
максимальна сила, яка діє на точкуFmax=2мН.
Записати рівняння цих коливань, якщо
період
![]() Початкову фазу вважати
φ0=
0.
Початкову фазу вважати
φ0=
0.
Розв’язання.
Рівняння гармонічного коливання має вигляд (4.23)
![]() (1)
(1)
Треба
знайти циклічну частоту
![]() і
амплітуду А.
і
амплітуду А.
Згідно
з (4.27)
![]() (2)
(2)
Відомо, що величина максимальної сили
![]()
де
amax
–
максимальне прискорення точки. З формули
(4.26) випливає, що величина максимального
прискорення точки
![]() ,
тоді
,
тоді
![]() (3)
(3)
Повна енергія точки (4.32)
![]() .
(4)
.
(4)
Розв`язуючи сумісно (3) і (4), знайдемо А.
![]() .
.
Переконаємось, що А має одиницю вимірювання м
![]() .
.
Знаходимо числове значення амплітуди.

Запишемо рівняння (1) з урахуванням того, що φ0 = 0;
![]() .
.
Відповідь:
![]() .
.
Приклад 7. Записати рівняння результуючого коливання, яке отримано складанням двох однаково напрямлених коливань
![]() і
і
![]() .
.
Розв’язання.
В результаті додавання цих коливань утворюється гармонічне коливання тієї ж частота з амплітудою (4.33).
![]() .
.
Оскільки j2-j2=p/2 і cosp/2=0,
![]() м
м
Початкова фаза результуючого коливання визначається з рівняння (4.34)
 ;
;
![]()
отже
![]()
Відповідь:
![]()
Приклад 8. Знайти логарифмічний декремент згасання δ для математичного маятника довжиною l=1м, якщо за час Dt = 1хв амплітуда його коливань зменшується у два рази.
Розв’язання.
За
визначенням
![]() .
Тому треба знайти коефіцієнт згасанняb
і період коливань Т. Запишемо амплітуду
згасаючих коливань згідно з (4.35) для
двох моментів часу t1
і t2:
.
Тому треба знайти коефіцієнт згасанняb
і період коливань Т. Запишемо амплітуду
згасаючих коливань згідно з (4.35) для
двох моментів часу t1
і t2:
![]() і
і
![]()
поділимо
А1
на А2:
![]() .
.
За
умовами задачі А1/А2=2
і t2-t1=Dt,
тому
![]() .
.
Логарифмуємо
цей вираз:
![]() .
.
Звідки

Період коливань знайдемо за формулою (4.29)
 .
.
Таким
чином
![]()
Відповідь: δ = 2,32×10-2.
Приклад 9. До електричної мережі напругою U=220В і частотою u=50 Гц підключено котушку опором R=100 Ом, яка споживає потужність Р=200 Вт. Знайти струм І, який протікає через котушку, а також її індуктивність L, якщо зсув фаз між напругою і струмом j=60°.
Розв’язання.
В умовах задачі йдеться про ефективні значення струму і напруги. Оскільки потужність змінного струму (4.46)
P
= Iеф
Ueф
cos
![]() .
.

Повний опір ділянки кола (4.44) з урахуванням того, що С=0.
![]() (1)
(1)
З іншого боку (4.43) повний опір
![]() (2)
(2)
Порівняємо
(1) і (2):
![]() =
=![]()
Розв’яжемо це рівняння відносно L:
 .
.
Оскільки
w=2pν,
 .
.
Перевіримо одиницю вимірювання:
![]()
Підставимо числові значення:

Відповідь: І=1,82 А, L=22 мГн.
Приклад 10. Рівняння незгасаючих коливань має вигляд у=5cos100pt і поширюється зі швидкістю V=300 м/с.
Знайти зміщення у від положення рівноваги точки, яка віддалена від джерела коливань на відстань х=3м у момент часу t=0,02 с після початку коливань, а також довжину хвилі l.
Розв’язання.
Згідно з (4.37)
![]() ,
,
тому зміщення
![]()
Довжина хвилі згідно з (4.38) l=vT.
Оскільки w = 100p, то Т = 2p/w = 0,02 с. Тоді l = 300 × 0,02 = 6 м. Відповідь: у = -5см, l = 6 м.
