Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесский национальный политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ЦИКЛЫ.doc

Скачиваний:

Добавлен:

10.02.2016

Размер:

1.29 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 66

Метод левых прямоугольников

Квадратурная формула:

, где.

Погрешность метода:

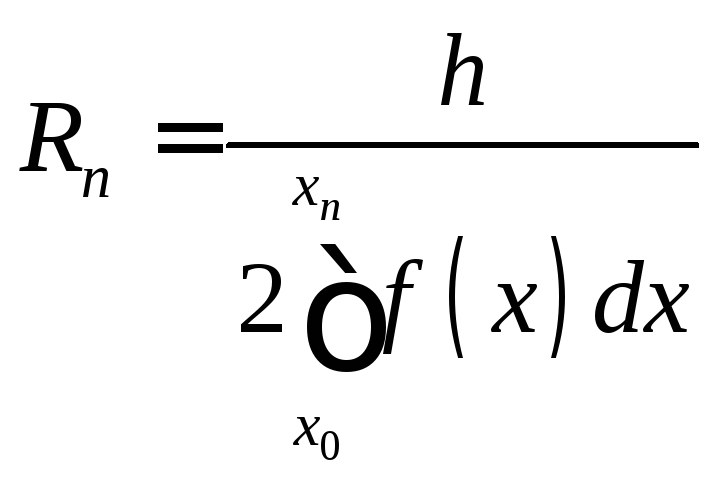, где.

Оценка точности вычислений в программе:

Метод левых прямоугольников точен для многочленов 1-го порядка.

Оценка точности вычислений для метода левых прямоугольников выполняется следующим образом.

Пусть ,.

Так как , имееми, так как, получаем.

Поскольку и, имеем соотношение, откуда, следовательно,.

Значит, .

Следовательно, как только выполнится условие , это будет означать, что, значит,является приближенным значением дляс точностью.

Метод трапеций

Квадратурная формула:

, где.

Погрешность метода:

, где.

, где,

Оценка точности вычислений в программе:

Метод трапеций точен для многочленов 1-го порядка.

Оценка точности вычислений для метода трапеций выполняется следующим образом.

Пусть — точное значение интеграла,— приближенное значение интеграла, полученное при разбиении отрезка интегрирования наравных частей,— приближенное значение интеграла при удвоенном числе точек разбиения,и— соответствующие погрешности,и— соответствующие шаги разбиения. Тогда, учитывая, что,, имееми, так как, получаем:.

Поскольку ,, имеем соотношение, откуда, следовательно,.

Значит, , или.

Следовательно, как только выполнится условие , это будет означить, что, то есть абсолютная погрешностьменьше(требуемой точности вычислений) и, значит,является приближенным значением дляс заданной степенью точности.

Метод Симпсона

Квадратурная формула:

, где.

Погрешность метода:

, где,,

, где.

Оценка точности вычислений в программе:

Метод Симпсона точен для многочленов до 3-го порядка включительно.

Примеры (на языке Pascal)

Пример 1. Найти сумму вводимых с клавиатуры положительных чисел. Сигналом к вычислению результата является ввод нуля, символизирующего конец последовательности.

Листинг 1.

var a,s: real;

BEGIN

s:=0;

read(a);

while a<>0 do

begin

if a>0 then s:=s+a;

read(a);

end;

writeln('Сумма = ',s);

END.

Пример 2. В бак нужно налить с помощью мерных сосудов различного объема столько жидкости, чтобы бак не переполнился, но был наполнен как можно полнее. Значения емкости бака, емкости сосуда, количества вылитых в бак мерных сосудов вводятся с клавиатуры. Если объем жидкости превышает объем бака, выдать соответствующее сообщение.

Листинг 2.

var v,v1,v2,k: integer;

BEGIN

write('Введите объем бака -> ');

readln(v);

v2:=0;

repeat

write('Введите объем мерного сосуда -> ');

readln(v1);

write('Введите кол-вовыливаемых сосудов -> ');

readln(k);

v2:=v2+v1*k;

writeln('Объем жидкости в баке = ',v2);

until v2>v;

if v2=v then

writeln('Бак наполнен!')

else writeln('Бак переполнен!');

END.

Пример 3. Найти сумму всех целых чисел, больших –50 и меньших 200, которые кратны 5 и 8 и заканчиваются на 5 или 0.

Листинг 3.

var i,s: integer;

BEGIN

s:=0;

for i:= –49 to 199 do

if (i mod 5 = 0) and (i mod 8 = 0)

and ((i mod 10 = 5) or (i mod 10 = 0)) then s:=s+i;

writeln('Сумма чисел, подходящих по условию= ',s);

END.

Пример 4. Дано натуральное число. Определить количество единиц в записи данного числа в двоичной системе счисления. Например, в двоичной записи числа 13 имеется 3 единицы (1101).

Листинг 4.

var n,x,k: integer;

BEGIN

repeat

write('Введите натуральное число -> ');

readln(n);

until n>0;

x:=1; k:=0;

while x<>0 do

begin

if n and x <> 0 then k:=k+1;

x:=x shl 1

end;

writeln('Количество двоичных единиц: ',k);

END.

Пример 5. Даны два натуральных числа. Определить их наибольший общий делитель.

Листинг 5.

var n,m,x: integer;

BEGIN

repeat

write('Введите натуральные числа m и n -> ');

readln(m,n);

until (n>0) and (m>0);

while n>0 do

begin

x:=m mod n;

m:=n;

n:=x

end;

writeln('НОД = ',m);

END.

Пример 6. Даны натуральные числаmиn. Определить их наименьшее общее кратное.

Листинг 6.

var i,n,m,k,nod,nok: integer;

BEGIN

write('Введите натуральное число n -> ');

readln(n);

write('Введите натуральное число m -> ');

readln(m);

if n>m then k:=m else k:=n;

nod:=1;

for i:=2 to k do

if (n mod i = 0) and (m mod i = 0) then

nod:=i;

nok:=nod*(n div nod)*(m div nod);

writeln('НОК чисел ',n,' и ',m,' = ',nok)

END.

Пример 7. Дано целое неотрицательное число. Определить количество нулей в его десятичной записи. Например, дляn= 103062 ответ 2.

Листинг 7.

var z: integer;

n: longint;

BEGIN

write('Введите целое неотрицательное число -> ');

readln(n);

if n=0 then z:=1 else

begin

z:=0;

while n>0 do

begin

if n mod 10 = 0 then z:=z+1;

n:=n div 10

end

end;

writeln('Количество нулей = ',z);

END.

Пример 8. Дано натуральное число. Заменить все цифры 7 в данном числе цифрами 8 и удалить из записи числа все единицы. Например, для 175718 новое число равно 8588.

Листинг 8.

var s,d: integer;

n,x: longint;

BEGIN

write('Введите натуральное число -> ');

readln(n);

x:=0; s:=1;

while n>0 do

begin

d:=n mod 10;

if d<>1 then

begin

if d=7 then d:=8;

x:=x+d*s;

s:=s*10

end;

n:=n div 10;

end;

if x=0 then writeln('Все цифры удалены')

else writeln('Новое число -> ',x);

END.

Пример 9. Дано натуральное число. Определить, образуют ли цифры числа симметричную последовательность, то есть читаются они одинаково слева направо и справа налево. Примером симметричной последовательности является число 012210.

Листинг 9.

var m,n,x: integer;

BEGIN

repeat

write('Введите натуральное число -> ');

readln(n);

until n>0;

m:=n; x:=0;

while n>0 do

begin

x:=x*10+n mod 10;

n:=n div 10

end;

if x=m then writeln('Палиндром')

else writeln('Не палиндром');

END.

Пример 10. Вывести на экран числа Фибоначчи от 1 доn. Каждое число последовательности из чисел Фибоначчи, начиная с третьего, получается сложением двух предыдущих чисел. Например: 1, 1, 2, 3, 5, 8, 13, 21 …

Листинг 10.

var a,b,c,i,n: integer;

BEGIN

write('Введите число N -> ');

readln(n);

a:=1; b:=1;

write(a,' ',b);

i:=3;

repeat

c:=a+b;

write(' ',c);

a:=b;

b:=c;

i:=i+1

until i>n

END.

Пример 11. Дано натуральное числоn. Определить, является лиnчислом Фибоначчи, то есть является ли оно элементом последовательности: 1, 1, 2, 3, 5, 8, 13, 21, 34, … .

Листинг 11.

var n,a,b,c: integer;

BEGIN

repeat

write('Введите натуральное число -> ');

readln(n);

until n>0;

a:=1; b:=1; c:=1;

while c<n do

begin

c:=a+b;

a:=b;

b:=c

end;

if c=n then writeln('Число Фибоначчи')

else writeln('Не число Фибоначчи');

END.

Пример 12. На интервале [2;n] найти натуральное число с максимальной сумой делителей.

Листинг 12.

var n,i,sum_max,sum,k,ch: integer;

BEGIN

write('Введите число n -> ');

readln(n);

sum_max:=1; ch:=1;

for i:=2 to n do

begin

sum:=0;

for k:=1 to i div 2 + 1 do

if i mod k = 0 then sum:=sum+k;

sum:=sum+i;

if sum>sum_max then

begin

sum_max:=sum;

ch:=i

end;

writeln('Максимальную сумму делителей ',sum_max,

' имеет число ',ch)

END.

Пример 13. Вычислить .

Листинг 13.

var n,s,i: integer;

BEGIN

write('Введите значение n -> ');

readln(n);

s:=0;

for i:=1 to n do s:=s+i;

writeln('Сумма = ',s);

END.

Пример 1 Вычислить функцию.

Листинг 1

var n,i,j,k: integer;

f: real;

BEGIN

write('Введите значение n -> ');

readln(n);

f:=1;

for i:=1 to n do

begin

k:=1;

for j:=1 to i do k:=k*j;

f:=f+1/k;

end;

writeln('Значение функции = ',f:7:5);

END.

Пример 15. Вычислить.

Листинг 15.

var n,i: integer;

s: real;

BEGIN

write('Введите натуральное число N -> ');

readln(n);

s:=0;

for i:=n downto 1 do

s:=sqrt(2+s);

writeln('Сумма = ',s)

END.

Пример 16.Дано натуральное числоn. Вычислить.

Листинг 16.

{$N+}

var s: extended;

i,n: byte;

BEGIN

write('Введите количество корней n -> ');

readln(n);

s:=0;

for i:=n downto 1 do

s:=sqrt(2*i+s);

writeln(s);

END.

Пример 17. Вычислить значение дроби, еслиaиnзаданы:.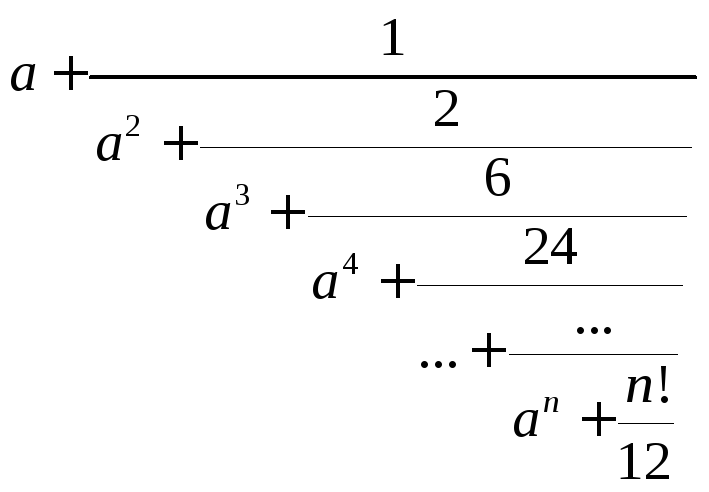

Листинг 17.

var a,n,i: integer;

p1,p2,y: real;

BEGIN

write('Введите a и n -> ');

readln(a,n);

p1:=1; p2:=1;

for i:=1 to n do

begin

p1:=p1*i;

p2:=p2*a

end;

y:=p2+(p1/12);

for i:=n downto 2 do

begin

p1:=p1/i;

p2:=p2/a;

y:=p2+p1/y;

end;

writeln(y:8:6)

END.

Пример 18. Вычислить значение дроби при заданном значенииx:.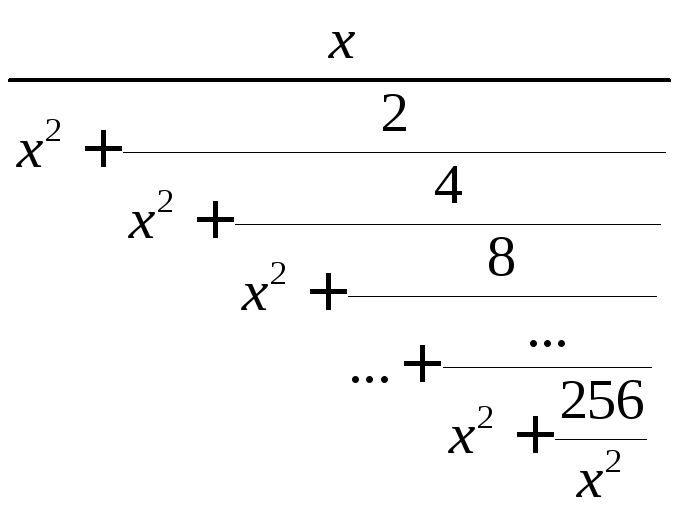

Листинг 18.

var x: integer;

y: real;

i,k: integer;

BEGIN

write('Введите число x -> ');

readln(x);

y:=(x*x)+256/(x*x);

k:=256 div 2;

for i:= k downto 2 do

begin

y:=sqr(x)+i/y;

k:=k div 2;

end;

y:=x/y;

writeln(y:6:4);

END.

Пример 19. Вычислить значение дроби при заданном значенииn:.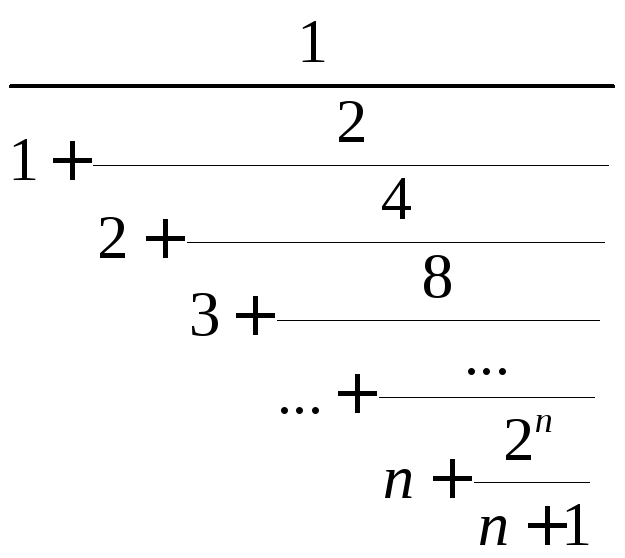

Листинг 19.

var n,i: integer;

p,y: real;

BEGIN

write('Введите число n -> ');

readln(n);

p:=1;

for i:=1 to n do

p:=p*2;

y:=n+p/(n+1);

for i:=n downto 2 do

begin

p:=p/2;

y:=(i–1)+p/y

end;

y:=1/y;

writeln(y:8:6);

END.

Пример 20. Дано вещественное число. С заданной точностьювычислить сумму членов бесконечного ряда:.

Листинг 20.

label 1;

var y,x,p1,a,s,eps: real;

p2,k,l: integer;

BEGIN

write('Введите x -> ');

readln(x);

write('Введите точность -> ');

readln(eps);

s:=0; p1:=x*x*x; p2:=1; k:=1;

y:=x*x*x*x; l:=–1;

1: p1:=p1*y; p2:=p2*(2*k+1)*2*k;

a:=l*p1/(p2*(4*k+3));

if abs(a)<eps then writeln('Сумма = ',s:8:6)

else

begin

s:=s+a; l:=–l;

k:=k+1;

goto 1

end;

END.

Пример 21. Составить программу для вычисления значения членов бесконечного рядадо члена рядас использованием циклаrepeat.

Листинг 21.

var y,x,eps: real;

n: integer;

BEGIN

write('Введите x и точность вычисления -> ');

readln(x,eps);

n:=1; y:=1;

repeat

y:=y*x/n;

writeln(y:8:6);

n:=n+1;

until abs(y) < eps

END.

Пример 22.Составить программу для вычисления суммы членов бесконечного рядас точностью до члена ряда, меньшего.

Листинг 22.

var y,z,x,eps: real;

c,f,n: integer;

BEGIN

write('Введите зн-ние х и точность вычисления -> ');

readln(x,eps);

y:=1; z:=1; n:=1; f:=1;

repeat

f:=f*2*n;

if odd(n) then c:=–1 else c:=1;

y:=exp(2*n*ln(x))/f;

z:=z+c*y;

n:=n+1

until abs(y) > eps;

write(z:8:6)

END.

Пример 23.Вычислить сумму членов бесконечного ряда. Вычисления прекратить, как только значение очередного члена ряда станет по модулю меньше заданной заранее погрешности.

При вычислении в подобных алгоритмах целесообразно воспользоваться рекуррентным соотношением (рекурсия будет рассмотрена дальше), позволяющим очередное значение члена ряда h_Nопределять из предыдущегоh_N_–1путем его умножения на некоторое приращение. Приращениенесложно получить, разделивh_Nнаh_N_–1. Эти значения равныи, следовательно. Учитывая, что,и, каждый последующий член рассматриваемого ряда может быть получен простым перемножением значения предыдущего члена ряда на найденное приращение с использованием операции присваивания. Как видим, эта операция избавила нас от необходимости вычисления факториалаN! иN-й степени числаx, что существенно уменьшило количество производимых операций и повысило точность вычислений.

Листинг 23.

var h,s,x,eps: real;

n: integer;

BEGIN

write('Введите значение x = ');

readln(x);

write('Введите точность вычисления -> ');

readln(eps);

h:=x; s:=x; n:=1;

while abs(h) >=eps do

begin

n:=n+1;

h:=(–x/n)*h;

s:=s+h

end;

writeln(s:8:6);

END.

Пример 2Среди чисел 1 <n< 100 найти все пары чисел, для которых их сумма равна их произведению.

Листинг 2

var k,a,b: integer;

BEGIN

k:=0;

for a:=1 to 100 do

for b:=1 to 100 do

begin

if a+b=a*b then

begin

k:=k+1;

writeln('Числа ',a,' ',b)

end

end;

if k=0 then writeln('Таких чисел нет')

else writeln('k = ',k);

END.

Пример 25.Определить, сколько изnзаданных точек принадлежит графику функцииy= |x|.

Листинг 25.

var k,i,n: integer;

x,y: real;

BEGIN

write('Введите количество точек N -> ');

readln(n);

k:=0;

for i:=1 to n do

begin

write('Введите к-ты ',i,'-ой точки (x,y) -> ');

readln(x,y);

if y=abs(x) then k:=k+1

end;

if k=0 then writeln ('Таких точек нет!')

else writeln('k = ',k)

END.

Пример 26. Подсчитать сумму всех нечетных чисел от 101 до 301.

Листинг 26.

var s,i: integer;

BEGIN

s:=0;

i:=101;

while i<=301 do

begin

s:=s+i;

i:=i+2

end;

writeln('Сумма кубов неч.чисел от 101 до 301 = ',s)

END.

Пример 27. Приитабулировать функцию. Значениеxизменяется от 1 до 5 с шагом 0,5.

Листинг 27.

const a=1.5; b=–3;

var r,x,s,y: real;

BEGIN

x:=1;

while x<=5 do

begin

r:=(2*a–x);

s:=b+2*x;

if (r=0) or (s<0)

then writeln ('При х = ',x,' решений нет!')

else

begin

y:=5*sqr(sin(2*sqr(x)*x))/r+12.5*sqrt(s);

writeln('При х = ',x,' y = ',y);

end;

x:=x+0.5

end

END.

Пример 28. Приитабулировать функцию. Для переменнойпоследовательно ввести значения 1, 2, 4, 7, 11, 17.

Листинг 28.

const a=2.7; b=0.4;

var p,x,q,y: real;

i: integer;

BEGIN

for i:=1 to 6 do

begin

write('Введите значение x -> ');

readln(x);

p:=6–3*a*sin(x);

q:=1+0.5*cos(b*x);

if (p<0) or (q=0)

then writeln ('Решения нет!')

else

begin

y:=12*a*x–3*b*sqr(p)/q;

writeln('При х = ',x,' y = ',y)

end

END.

Пример 29. Дано натуральное числоn. Разложить его на простые множители.

Листинг 29.

var i,n,f,j: integer;

BEGIN

write('Введите натуральное число n -> ');

readln(n);

write(n,'= 1');

f:=0; j:=n;

for i:=2 to n div 2 do

begin

if j mod i = 0 then

begin

f:=1;

while j mod i = 0 do

begin

write(' * ',i);

j:=j div i

end

end;

if f=0 then writeln(' * ',n) else writeln

END.

Пример 30. Вводится последовательность изnцелых чисел. Найти сумму всех отрицательных чисел.

Листинг 30.

var i,n,x,s: integer;

BEGIN

write('Введите длину последовательности -> ');

readln(n);

s:=0;

for i:=1 to n do

begin

write('Введите ',i,' число x -> ');

readln(x);

if x<0 then s:=s+x;

end;

if s = 0 then

writeln('Отрицательных чисел нет!')

elsewriteln('Сумма отрицательных чисел = ',s);

END.

Пример 31. На выставке собак, где были представлены разные породы, отбор животных производился по возрасту и высоте холки. Определить, сколько было боксеров 2–3-летнего возраста с высотой холки не менее 55 см.

Листинг 31.

var por: string;

n,i,k: integer;

a,l: real;

BEGIN

write('Введите длину последовательности -> ');

readln(n);

k:=0;

for i:=1 to n do

begin

write('Порода, возраст, высотахолки -> ');

readln(por,a,l);

if (por='боксер') and (a<=3) and (a>=2)

and (l>=55) then k:=k+1;

end;

if k = 0 then writeln('Таких собак нет!')

else

writeln('Боксеров 2–3 лет с высотой холки не ниже

55 см ',k);

END.

Пример 32. Вычислить сумму и произведение 10 членов арифметической прогрессии 2, 5, 8, 11, … .

Для определения значения очередного члена прогрессии будем использовать формулу x=a+d (n– 1), гдеa— член арифметической прогрессии,d — ее разность, аn — длина прогрессии.

Листинг 32.

const a=2; d=3;

var n,i,k,x,s,p: integer;

BEGIN

p:=1;

write('Введите число членов арифм.прогр.-> ');

readln(k);

for n:=1 to k do

begin

x:=a+d*(n–1);

s:=s+x;

p:=p*x;

end;

write('При k = ',k,' s = ',s,' p = ',p);

END.

Пример 33.Написать программу определения номера члена геометрической прогрессии 2, 4, 8, 16, …, превышающего числоz.

Листинг 33.

var a,z,d,n,q: integer;

Ма x: real;

BEGIN

write ('Введите значение z:> ');

readln(z);

a:=2; q:=2;

repeat

x:=a*exp(n*ln(q));

writeln(x);

n:=n+1;

until x>z;

write('x = ',x,' n = ',n);

END.

Пример 3Математик и астроном Кеплер обратил внимание на то, что с увеличением номеров элементов числового ряда Фибоначчи отношение предыдущего элемента к последующему приближается к отношению золотого сечения (0,618). Написать программу проверки этого утверждения.

Листинг 3

var a,b,k,c: integer;

p,q,eps: real;

BEGIN

a:=1; b:=1; eps:=10E–6;

repeat

p:=q;

q:=a/b;

c:=b;

b:=a+b;

a:=c;

k:=k+1;

until abs(p–q)<eps;

write('a = ',a,' b = ',b,' p = ',p:8:6,

' q = ',q:8:6,' k = ',k)

END.

Пример 35. Написать программу, помогающую вкладчику узнать: сколько лет нужно ожидать суммыS, если начальный вклад равенVприPпроцентах прироста вклада за год.

Листинг 35.

var k: integer;

v,p,s,w,q: real;

BEGIN

writeln('Введите вклад, процент за год,

требуемую сумму через пробел');

read(v,p,s);

w:=v;

repeat

q:=v*p/100;

v:=v+q;

k:=k+1;

until v>s;

writeln('При вкладе ',w,' сумма ',s,' будет

накоплена за ',k,' лет');

END.

Пример 36. Существуют числа, обладающие следующими свойствами:

число делится на все свои цифры;
число, полученное из данного записью цифр в обратном порядке, тоже делится на все свои цифры.

Примером такого числа является 216. Составить программу нахождения всех трехзначных чисел, обладающих этими свойствами, при этом числа с одинаковыми первой и последней цифрами не рассматривать.

Листинг 36.

var k,l,c,a,b: integer;

BEGIN

for k:=1 to 9 do

for l:=1 to 9 do

for c:=1 to 9 do

if k<>c then begin

a:=k*100+l*10+c;

if a mod k = 0 and a mod l = 0

and a mod c = 0

then begin

b:=c*100+l*10+k;

if b mod k = 0 and b mod l = 0

and b mod c = 0

then writeln(a);

end;

end

END.

Пример 37. Дано натуральное числоn< 99. Получить все способы выплаты суммыnс помощью монет достоинством 1, 2, 10 и 20 копеек.

Листинг 37.

var n,i,j,l,k,k1,k2,k3,k4,s: integer;

BEGIN

write('Введите n -> ');

readln(n);

k1:=n; k2:=n div 2; k3:=n div 10; k4:=n div 20;

for i:=0 to k4 do

for j:=0 to k3 do

for k:=0 to k2 do

for l:=0 to k1 do

begin

s:=i*20+j*10+k*2+l;

if s=n then

begin

writeln('"1" - ',l);

writeln('"2" - ',k);

writeln('"10" - ',j);

writeln('"20" - ',i);

writeln

end

END.

Пример 38. Составить программу для нахождения значения функциипри изменении аргументаxв интервале от 0 доcс шагомh.

Листинг 38.

var a,b,c,om,fi,h,y,ymin,x: real;

k,i: integer;

BEGIN

write('Введите значения a,b,c,omega,fi и h -> ');

readln(a,b,c,om,fi,h);

ymin:=1E19;

k:=trunc(c/h)+1;

x:=0;

for i:=1 to k do

begin

y:=a*exp(–b*x)*sin(om*x+fi);

if y < ymin then ymin:=y;

x:=x+h

end;

write('y min = ',ymin:8:6);

END.

В этой же программе, но с инструкцией whileбудет отсутствовать описание переменныхkиi, а сам цикл примет вид:

while x<=c do

begin

y:=a*exp(–b*x)*sin(om*x+fi);

if y < ymin then ymin:=y;

x:=x+h

end;

Пример 39. Составить программу для нахождения экстремального значения функциипри изменении аргументаотдос шагом.

Листинг 39.

var a,b,c,h,x,xn,xk,y,ym: real;

i,n,k: integer;

BEGIN

write('Введите значения a,b,c,h,xn,xk -> ');

readln(a,b,c,h,xn,xk);

k:=trunc((xk–xn)/h)+1;

if c>0 then n:=1 else n:=–1;

ym:=n*1E19;

x:=xn;

for i:=1 to k do

begin

y:=abs(a)*exp(b*x+c*x*x);

if n*y<n*ym then ym:=y

else writeln(ym:8:6, y:8:6);

x:=x+h

end;

writeln(ym:8:6, y:8:6);

END.

Пример 40. Составить программу для вычисления наименьшего положительного корня уравненияс точностью до.

Листинг 40.

var x0,x1,x2,eps: real;

BEGIN

write('Введите значения x0 и eps -> ');

readln(x0,eps);

repeat

x1:=arctan(x0)+pi;

x0:=x1;

x2:=x1;

until abs(x2–x1)<eps;

write(x1,x2)

END.

Пример 41. Составить программу нахождения корня уравненияметодом деления пополам на отрезке от 0,4 до 1 с точностью.

Листинг 41.

label 1;

var a,b,dx,fa,fb,fx,x,eps: real;

BEGIN

write('Введите значение a,b и eps -> ');

readln(a,b,eps);

fa:=a+sqrt(a)+exp(1/3*ln(a))-2.5;

fb:=b+sqrt(b)+exp(1/3*ln(b))-2.5;

if fa*fb>0 then

begin

writeln('Корней нет!');

exit

end;

1: x:=(a+b)/2;

dx:=(b-a)/2;

if dx<=eps then

begin

writeln('x = ',x);

exit

end

else

fx:=x+sqrt(x)+exp(1/3*ln(x))-2.5;

if fx*fa>0 then

begin

a:=x;

goto 1

end

else if fx*fa<0 then

begin

b:=x;

goto 1

end;

END.

Пример 42. Методом итераций найти корень уравнения, расположенный на отрезке, с абсолютной погрешностью. Напечатать число итераций, необходимых для вычисления корня.

Заданное уравнение преобразуем к виду следующим образом:

;

Проверка условия сходимости метода итераций: . Очевидно, чтодля всех. Следовательно, рассматриваемый процесс итераций сходится.

Листинг 42.

var a,b,x1,x0,delta,eps: real;

n: integer;

BEGIN

write('Введите значения a, b, eps -> ');

readln(a,b,eps);

x0:=(a+b)/2; n:=0;

repeat

x1:=0.5*sin(x0*x0–1);

n:=n+1;

delta:=abs(x1–x0);

x0:=x1

until delta<eps;

writeln('Корень = ',x1:8:6);

writeln('Число итераций = ',n);

END.

Пример 43. Вычислить с заданной точностьюминимальное значение функциина интервале. Шаг изменения аргумента принять равным. Вывести вычисленное значение и значение аргумента, при котором оно достигается.

Листинг 43.

const eps=10e–5;

var a,b,x0,xmin,y,ymin,x,h: real;

BEGIN

write('Введите a, b -> ');

readln(a,b);

x0:=a; h:=0.15;

while h>=eps do

begin

ymin:=10e10; x:=x0;

repeat

y:=x*sqr(x–1)*sqr(x–2)*(x–2);

if y<ymin then

begin

ymin:=y;

xmin:=x

end;

x:=x+h

until y>ymin;

x0:=xmin–h;

h:=h/2

end;

writeln('xmin = ',xmin:8:6,' ymin = ',ymin:8:6)

END.

Пример 44. Дано вещественное положительное число. Вычислить с точностьюплощадь фигуры, заключенной между дугами двух кривых:[16].

Воспользуемся численными методами решения уравнений и интегрирования.

При составлении программы будем придерживаться следующего алгоритма.

Построим чертеж к задаче на экране монитора.
Для уточнения корней воспользуемся одним из методов приближенного нахождения корней уравнения, например методом проб (метод деления отрезка пополам). Вычислим корни уравнения 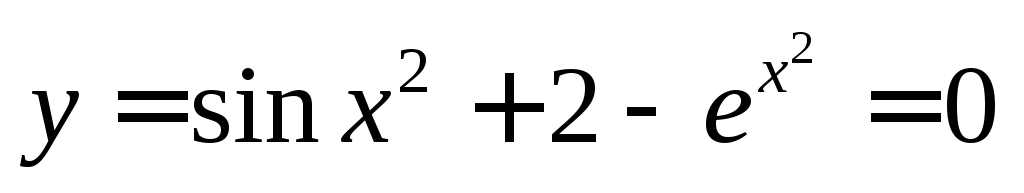с точностью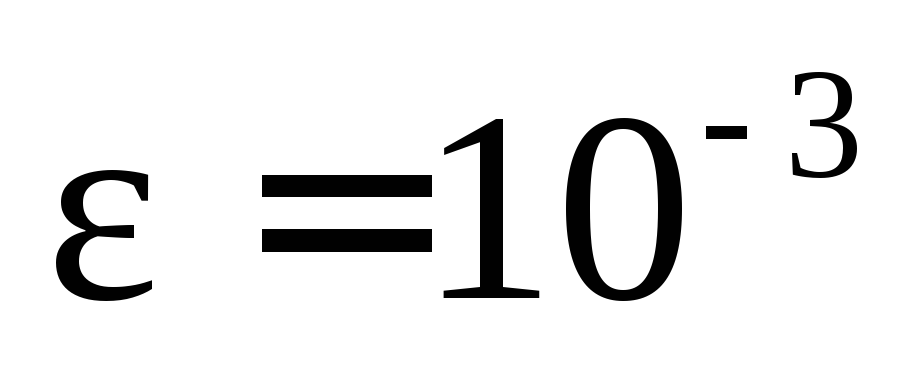. Используем подпрограмму уточнения корней.

ВНИМАНИЕ

В этой задаче были использованы подрограммы. Подробнее о них будет рассказано позже, в следующей теме.

Найдем площадь фигуры, заключенной между дугами двух кривых, как разность площадей криволинейных трапеций. Зная пределы интегрирования, воспользуемся методом Симпсона для приближенного вычисления интегралов.

Листинг 44.

uses graph;

var

grdriver, grmode, errcode, i, h: integer;

a,b,e,c,d,x,y,k: real;

i1,i2,h1,m,n,s: real;

function fn(t: real): real;

begin

fn:=sin(sqr(t))+2–exp(t*t);

end;

function kor(l: real; k: real): real;

var s: real;

begin

if fn(l)=0 then s:=1

else if fn(k)=0 then s:=k

else

begin

repeat

s:=(l+k)/2;

if fn(s)=0 then s:=(l+k)/2

else if fn(l)*fn(s)>0

then l:=s

else k:=s;

until abs(k–l)<e;

s:=(l+k)/2;

kor:=s;

end;

BEGIN

grdriver:=detect;

initgraph(grdriver,grmode,'');

errcode:=graphresult;

if errcode=grok then

begin

setcolor(5);

line(0,160,630,160);

line(140,0,140,350);

h:=40;

i:=20;

repeat

line(i,158,i,162);

i:=i+h

until i>630;

h:=40;

i:=40;

repeat

line(138,i,142,i);

i:=i+h

until i>=350;

x:=–2;

k:=0.01;

while x<=3 do

begin

putpixel(140+trunc(40*x),

160–trunc(40*(sin(sqr(x))+2)),5);

putpixel(140+trunc(40*x),

160–trunc(40*exp(x*x)),5);

x:=x+k

end;

readln;

closegraph;

end

else halt(1);

writeln('Укажите точность вычисления

пределов интегрирования');

readln(e);

repeat

writeln('Укажите концы первого отрезка');

read(c,d);

until fn(c)*fn(d)<=0;

a:=kor(c,d);

repeat

writeln('Укажите конца второго отрезка');

read(c,d);

until fn(c)*fn(d)<=0;

b:=kor(c,d);

writeln(a);

writeln(b);

writeln('Укажите точность вычисления интеграла');

readln(e);

writeln('Укажите число узлов интерполяции');

readln(n);

i1:=0;

repeat

n:=n*2;

h1:=(b–a)/n;

s:=fn(a)+fn(b);

x:=a+h1;

repeat

s:=s+4*fn(x)+2*fn(x+h1);

x:=x+2*h1

until x>=b;

i2:=h1/3*s;

m:=abs(i1–i2);

i1:=i2;

until M<=15*e;

writeln(Искомая площадь ',i2);

readln;

END.

Пример 45. Составить программу для вычисления значения определенного интегралас точностью.

Листинг 45.

label 1,2;

var a,b,hx,s1,s2,x,ya,yb,y,eps: real;

n: integer;

BEGIN

write('Введите n, a, b, eps -> ');

readln(n,a,b,eps);

ya:=exp(a–a*a)/a;

yb:=exp(b–b*b)/b;

s1:=0;

1: s2:=(ya+yb)/2;

x:=a;

hx:=(b–a)/n;

while x<=b do

begin

x:=x+hx;

y:=exp(x–x*x);

s2:=s2+y

end;

s2:=s2+hx;

if abs(s1–s2)<=eps

then

begin

writeln(s2);

goto 2

end

else

begin

s1:=s2;

n:=2*n;

goto 1

end;

2: END.

Пример 46. Вычислить методом трапеций значение интеграладля,,, разбивая отрезок интегрирования на 60 частей. Для контроля вычислить точное значение интеграла и оценить относительную погрешность метода.

Вычислить точное значение интеграла для .

Листинг 46.

var a,b,k,x,z,zt,dz,dx: real;

n,i: integer;

BEGIN

write('Введите a, b, n -> ');

readln(a,b,n);

k:=0.5;

z:=(sqr(sin(a))/(1+2*k*cos(a)+k*k)+

sqr(sin(b))/(1+2*k*cos(b)+k*k))/2;

dx:=(b–a)/n; x:=a;

for i:=1 to n-1 do

begin

x:=x+dx;

z:=z+sqr(sin(x))/(1+2*k*cos(x)+k*k)

end;

z:=z*dx;

zt:=pi/2;

dz:=abs(zt-z)*100;

writeln('Приближенное значение z = ',z:8:6);

writeln('Точное значение zt = ',zt:8:6);

writeln('Относительная погрешность ',dz:8:6)

END.

Пример 47. Вычислить методом трапеций значение интегралас точностьюдля,,. Для контроля вычислить точное значение интеграла и оценить абсолютную погрешность вычисления.