Лекция № 5 Невозмущённое движение искусственного спутника Земли.

1. Дифференциальные уравнения невозмущённого движения.

2. Элементы орбиты и законы Кеплера. Основные формулы невозмущённого движения.

3. Вычисление положения и скорости спутника по Кеплеровым элементам орбиты.

Траектория, по которой движется в полёте искусственный спутник Земли (космический аппарат (КА), небесное тело), называется отбитой. В зависимости от характера сил, действующих на спутник в полёте, траекторию делят на участки, где действуют гравитационные и инерционные силы, и участки, где дополнительно прикладывается вектор силы от бортовых двигателей. Первый вид движения называется свободным полётом, второй вид – активным движением, или маневрированием.

Если при определении траектории движения спутника подразумевают его движение под действием только силы притяжения Земли, с одним притягивающим центром в центре масс Земли, то такое движение называют невозмущённым или Кеплеровым.

Если при определении траекторного движения спутника учитывают возмущающие силы, такие как притяжение Луны и Солнца, давление светового излучения, неравномерность гравитационного поля Земли и другие, то такое движение называется возмущённым.

1. Дифференциальные уравнения невозмущённого движения.

Рассмотрим движение спутника с массойвокруг Земли. Землю будем считать точечной массой или шаром с массойсо сферически симметричным распределением плотности. В таком гравитационном поле отвесные линии являются прямыми, направленными к центру сферы. Массу спутникабудем считать ничтожно малой по сравнению с массой Земли. В дополнении к этим условиям, будем также считать, что на движение спутника не влияют никакие другие силы, кроме притяжения Земли. При таких условиях задача о движении спутника в небесной механике называется ограниченной задачей двух тел.

Начало инерциальной системы координат поместим в геоцентр. В этой системе положение спутника будем задавать его радиусом-вектором, скорость – вектором, а ускорение – вектором а:

Точками над символами обозначается дифференцирование по времени, то есть одна точка – производная первого порядка, две точки – производная второго порядка и т. д.

Центральное гравитационное поле Земли характеризуется потенциалом

Вызывающее в движении спутника ускорение, равное по абсолютной величине

где геоцентрическая гравитационная постоянная, арасстояние спутника от геоцентра. Вектор ускорения ,который, как и вектор силы ,направлен по радиусу-вектору к центру масс Земли, получаем путём умножения на единичный вектор ,то есть

Полученное дифференциальное уравнение описывает невозмущённое, или Кеплерово, движение. Это уравнение в координатной форме записывается в виде системы обыкновенных дифференциальных уравнений 2-го порядка:

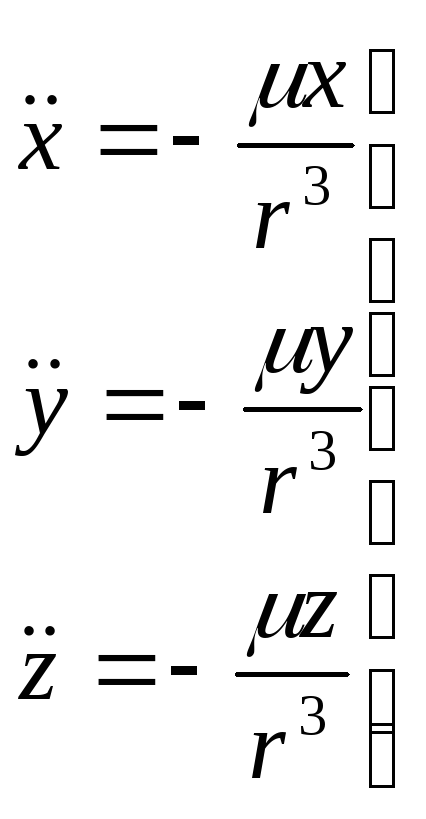
Данные уравнения должны иметь шесть независимых постоянных интегрирования, которые позволяли бы вычислять на любой момент положение и скорости спутника.

Первые интегралы определяющие закономерности невозмущённого движения.

1. Векторный интеграл площадей:

–

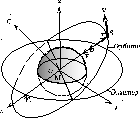
Орбита в пространстве

Орбита в плоскости орбиты

Постоянный вектор С является вектором кинетического момента спутника, направленным по нормали к плоскости отбиты, а его компонентыявляются проекциями кинетического момента на координатные оси. Вектор С задаёт ориентировку плоскости орбиты в пространстве. Орбитальное движение происходит в плоскости, проходящей через центр, а сама отбита является плоской кривой.

2. Интеграл энергии:

где постоянная энергии. Умножение уравнения надаёт:

откуда видно, что полная энергия равная сумме кинетической и потенциальной энергий остаётся постоянной.

3. Векторный интеграл Лапласа:

Постоянный вектор называется вектором Лапласа. Он находится в плоскости орбиты и направлен в ближайшую к центральному телу точку орбиты спутника, называемую перигеем. Противоположная ему, наиболее удалённая от геоцентра точка орбиты, называется апогеем, а соединяющая их линияназывается линией аспид. Линия, по которой пересекаются плоскости экватора и орбиты, называется линией узлов. В восходящем узле спутник пересекает плоскость экватора, переходя из южного полушария небесной сферы в северное. В нисходящем узле спутник переходит из северного полушария в южное.

Первые интегралы связаны соотношениями: